Hidden Markov Model

Posted 2020-08-31

What‘s HMM?

    In problems that have an inherent temporality -- that is, consist of a process that unfolds in time -- we may have states at time t that are influenced directly by a state t-1. Hidden Markov model (HMM) have found greatest use in such problem, for instance speech recognition or gesture recongnition.

    HMM has two stochastic process. One is a Markov chain and the other is a "emission" that based on each Markov chain‘s state.

    The Markov chain can be decribed as Figure 1

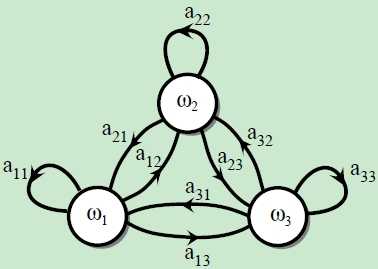
Figure 1

    The state space in Markov chain is $\\mathbf{W}$
\\[
\\mathbf{W} = \\{w_1, w_2, ..., w_n\\}
\\]

    The state at time t is $w(t)$ and a particular sequence of length T is denoted by $\\mathbf{w^T}$.
\\[
\\mathbf{w^T} = \\{w(1), w(2), ..., w(T) \\}
\\]

    where $w(t) = w_i$, $i = 1,2,...,n$

    The hidden Markov model can be described as Figure 2.

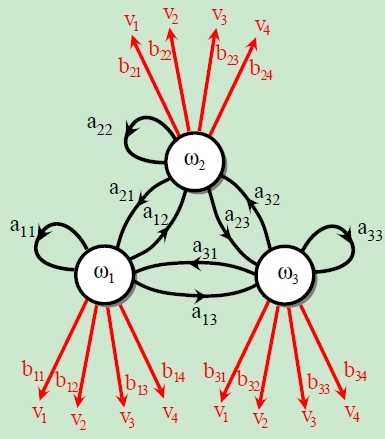
Figure 2

    At every time step t the system is in a state $w(t)$ but now it emits some (visible) symbol $v(t)$. Notice that $v(t)$ can be discrete or continuous, but in the passage, $v(t)$ is assumed to be discrete.

    We define a particular sequence of such visible states as
\\[\\mathbf{V^T} = \\{v(1), v(2), ..., v(T)\\}\\]

    where $v(t) = v_i$, $i=1,2,3,...$

    We denote the initial distrubution $\\pi_i$, transition probabilities $a_{ij}$ among hidden states and for the probability $b_{jk}$ of the emission of a visible state:
\\[
\\begin{split}
& \\pi_i = P(w(1)=w_i) \\\\
& a_{ij}(t) = P\\left(w(t+1)=w_j|w(t)=w_i\\right)\\\\
& b_{jk}(t) = P\\left(v(t)=v_k|w(t)=w_j\\right)
\\end{split}
\\]

    We have the normalization condition:
\\[
\\begin{split}
& \\sum_{j}a_{ij}(t) = 1\\\\
& \\sum_{k}b_{jk}(t) = 1
\\end{split}
\\]

    Let $\\mathbf{A}=[a_{ij}]_{n\\times n}$ , $\\mathbf{B}=[b_{jk}]_{n\\times m}$ and $\\mathbf{\\pi} = (\\pi_i)$, then the HMM can be described as $\\mathbf{\\lambda} = (\\mathbf{A},\\mathbf{B},\\mathbf{\\pi})$

Three Central Issues

    When we get an HMM we need to handle three central issues in order to make full use of HMM　and have a better understanding of HMM.

    ① The Evaluation problem

    Suppose we have an HMM. Determine the probability that a particular sequence of visible states $\\mathbf{V^T}$ generated by that model.

    ② The Learning problem

Suppose we are given the coarse structure of a model (the number of hidden states and the number of visible states) but not the probability $a_{ij}$, $b_{jk}$ and $\\pi_i$. Given a set of training observation of visible symbols, determine these parameters.

    ③ The Decoding problem

    Suppose we have an HMM as well as a set of observation $\\mathbf{V^T}$. Determine the most likely sequence of hidden states $\\mathbf{w^T}$ that led to those observation.

    We will consider each of these problem in turn.

Evaluation problem

    Evaluation problem: Given $\\mathbf{\\lambda} = (\\mathbf{A},\\mathbf{B},\\mathbf{\\pi})$ and observation sequence $\\mathbf{V^T}$, compute $P(\\mathbf{V^T}|\\mathbf{\\lambda})$.

    If we compute $P(\\mathbf{V^T}|\\mathbf{\\lambda})$ directly:
\\[
\\begin{split}
P(\\mathbf{V^T}|\\mathbf{\\lambda}) &= \\sum_{\\mathbf{w^T}}P(\\mathbf{V^T}|\\mathbf{w^T},\\mathbf{\\lambda})P(\\mathbf{w^T}|\\mathbf{\\lambda})\\\\
& = \\sum_{\\mathbf{w^T}}\\prod_{t=1}^{T}\\pi_i a_{ij}(t) b_{jk}(t)
\\end{split}
\\]

    Analyze the formulation above, $w^T$ totally have $n^T$ situations. Thus, it is an $O(Tn^T)$ calculation, which is quite prohibitive in practice.

    A computationaly simpler algorithm -- forward algorithm and backward algorithm -- for the same goal is as follows. Notice that both forward algorithm and backward algorithm can calculate $P(\\mathbf{V^T}|\\mathbf{\\lambda})$.

Forward algorithm

    Define forward variable:
\\[
\\alpha_t(i) = P(V^t,w(t)=w_i|\\lambda)
\\]

   Then,
\\[
\\begin{split}
\\alpha_1(i) &= P(v(1)=v_k,w(1)=w_i|\\lambda) \\\\
& = P(v(1)=v_k|w(1)=w_i,\\lambda)P(w(1)=w_i|\\lambda)\\\\
& = \\pi_i b_{ik}(1)
\\end{split}
\\]
\\[
\\begin{split}
\\alpha_{t+1}(j) &= \\left[ \\sum_{i=1}^{N}\\alpha_t(i)a_{ij}(t) \\right] b_{jk}(t+1)\\\\
1\\leq &t\\leq T-1, \\qquad 1\\leq j\\leq n
\\end{split}
\\]

\\[
P(\\mathbf{V^T}|\\mathbf{\\lambda}) = \\sum_{i=1}^{n}\\alpha_T(i)
\\]

Backward algorithm

    Define backward varible:
\\[
\\begin{split}
\\beta_t(i) &= P(V^T/V^t|w(t)=w_i,\\lambda)\\\\
& = P(v(t+1),v(t+2),...,v(T)|w(t)=w_i,\\lambda)
\\end{split}
\\]

    Then,
\\[
\\begin{split}
\\beta_T(i) = 1
\\end{split}
\\]

\\[
\\begin{split}
\\beta_i(t) &= \\sum_{j=1}^{n}a_{ij}b_{jk}(t+1)\\beta_j(t+1)\\\\
1\\leq &t\\leq T-1, \\qquad 1\\leq i\\leq n
\\end{split}
\\]

\\[
\\begin{split}
P(\\mathbf{V^T}|\\mathbf{\\lambda}) & = \\sum_{i=1}^{n}\\pi_i b_{ik}(1) \\beta_1(i)\\\\
& = \\sum_{i=1}^{n}\\alpha_1(i) \\beta_1(i)
\\end{split}
\\]

    The complexity of both forward and backward algorithm is $O(Tn^2)$, rather than the direct algorithm‘s complexity $O(Tn^T)$ !

Some probability calculation

    ① Given $\\lambda$ and observation $V^T$, the probability of $w(t)=w_i$ is :
\\[
\\begin{split}
\\gamma_t(i) & = P(w(t)=w_i|V^T,\\lambda)\\\\
& = \\frac{P(w(t)=w_i,V^T|\\lambda)}{P(V^T|\\lambda)}\\\\
& = \\frac{\\alpha_t(i)\\beta_t(i)}{P(V^T|\\lambda)}\\\\
& = \\frac{\\alpha_t(i)\\beta_t(i)}{\\sum_{i=1}^{n}\\alpha_t(i)\\beta_t(i)}
\\end{split}
\\]

    ② Given $\\lambda$ and observation $V^T$, the probability of $w(t)=w_i\\cap w(t+1)=w_j$:
\\[
\\begin{split}
\\xi_t(i,j) &= P(w(t)=w_i,w(t+1)=w_j|V^T,\\lambda)\\\\
& = \\frac{P(w(t)=w_i,w(t+1)=w_j,V^T|\\lambda)}{P(V^T|\\lambda)}\\\\
& = \\frac{P(w(t)=w_i,w(t+1)=w_j,V^T|\\lambda)}{\\sum_{i=1}^{n}\\sum_{j=1}^{n}P(w(t)=w_i,w(t+1)=w_j,V^T|\\lambda)}\\\\
& = \\frac{\\alpha_t(i)a_{ij}b_{jk}(t+1)\\beta_{t+1}(j)}{\\sum_{i=1}^{n}\\sum_{j=1}^{n}\\alpha_t(i)a_{ij}b_{jk}(t+1)\\beta_{t+1}(j)}
\\end{split}
\\]

    ③ We can get some expectation value.

    (1) The expectation value of state i in condition of observation $V^T$:
\\[
\\sum_{t=1}^{T} = \\gamma_t(i)
\\]

    (2) The expectation value of the times that transform from state i to the another state:
\\[
\\sum_{t=1}^{T-1} = \\gamma_t(i)
\\]

    (3) The expectation value of the times that transform from state i to state j:
\\[
\\sum_{t=1}^{T-1} = \\xi_t(i,j)
\\]

Learning problem

    Learning problem : Given the observation $V^T$(obvious variable) without $w^T$(hidden variable), compute the parameters of $\\lambda = (A,B,\\pi)$.

    The parameter learining can be completed by EM algorithm(Also called Baum-Welch algorithm).

    The log likehood function of the hidden variable and obvious variable:
\\[
L = \\log P(V^T,w^T|\\lambda)
\\]

    The Q function can be writen as:
\\[
\\begin{split}
Q(\\lambda,\\lambda^0) &=\\sum_{w^T}\\log P(V^T,w^T|\\lambda) P(w^T|V^T,\\lambda^0) \\\\
& = \\sum_{w^T}\\log P(V^T,w^T|\\lambda) \\frac{P(V^T,w^T|\\lambda^0)}{P(V^T|\\lambda^0)}
\\end{split}
\\]

    Thus,
\\[
\\begin{split}
\\lambda &= arg\\max\\limits_{\\lambda}Q(\\lambda,\\lambda^0)\\\\
& = arg\\max\\limits_{\\lambda} \\sum_{w^T}\\log P(V^T,w^T|\\lambda) \\frac{P(V^T,w^T|\\lambda^0)}{P(V^T|\\lambda^0)}\\\\
& = arg\\max\\limits_{\\lambda} \\sum_{w^T}\\log P(V^T,w^T|\\lambda) P(V^T,w^T|\\lambda^0)
\\end{split}
\\]

    Finnaly, we can get:
\\[
\\begin{split}
a_{ij} &= \\frac{\\sum_{t=1}^{T-1}\\xi_t(i,j)}{\\sum_{t=1}^{T-1}\\gamma_t(i)}\\\\
b_{jk}(t) &= \\frac{\\sum_{t=1,v(t)=v_k}^{T}\\gamma_t(j)}{\\sum_{t=1}^{T}\\gamma_t(j)}\\\\
\\pi_i & = \\gamma_1(i)
\\end{split}
\\]

    Thus, Baum-Welch algorithm can be described as follows:

    ① Initialize. In terms of n=0, choose $a_{ij}^{(0)}$, $b_{jk}^{(0)}(t)$ and $\\pi_i^{(0)}$, and get $\\lambda{(0)}=(A^{(0)},B^{(0)},\\pi^{(0)})$

    ② Recursion. for n=1,2,...
\\[
\\begin{split}
a_{ij}^{(n+1)} &= \\frac{\\sum_{t=1}^{T-1}\\xi_t(i,j)}{\\sum_{t=1}^{T-1}\\gamma_t(i)}\\\\
b_{jk}^{(n+1)}(t) &= \\frac{\\sum_{t=1,v(t)=v_k}^{T}\\gamma_t(j)}{\\sum_{t=1}^{T}\\gamma_t(j)}\\\\
\\pi_i^{(n+1)} & = \\gamma_1(i)
\\end{split}
\\]

    ③ If satisfy the termination condition, algorithm done. Otherwise, go to \\ding{173}.

Decoding problem

    Decoding problem: Given the observation $V^T$ and model parameters $\\lambda = (A,B,\\pi)$, calculate the most likely hidden state $w^T$.

To solve decoding problem, we can use Viterbi algorithm, which is a dynamic programming.

    Define variable:
\\[
\\delta_t(i) = \\max\\limits_{w(1),...,w(t-1)}P(w(t)=w_i,w(t-1),...,w(1),v(t),...,v(1)|\\lambda), \\qquad i = 1,2,...,n
\\]

    then,
\\[
\\delta_{t+1}(j) = \\left[\\max\\limits_{i}\\delta_t(i)a_{ij}\\right]b_{jk}(t+1)
\\]

    Define variable:
\\[
\\psi_t(i) = \\arg\\max\\limits_{1\\leq j\\leq}[\\delta_{t-1}(j)a_{ji}]
\\]

    So, Vaterbi algorithm can be described as follows:

    ① Initialization.
\\[
\\begin{split}
\\delta_1(i) &= P(w(1)=w_i,v(1)|\\lambda)\\\\
& = P(v(1)=v_k|w(1)=w_i)P(w(1)=w_i)\\\\
& = \\pi_i b_{ik}(1), \\qquad i=1,2,...,n\\\\
\\psi_1(i) &= 0, \\qquad i=1,2,...,n
\\end{split}
\\]

    ② Recursion. For t=2,3,...,T
\\[
\\begin{split}
\\delta_{t}(i) &= \\left[\\max\\limits_{j}\\delta_{t-1}(j)a_{ji}\\right]b_{ik}(t), \\qquad i=1,2,...,n\\\\
\\psi_t(i) & = \\max\\limits_{j}\\delta_{t-1}(j)a_{ji}, \\qquad i=1,2,...,n
\\end{split}
\\]

    ③ Termination.
\\[
\\begin{split}
P^* &= \\max\\limits_{i}\\delta_T(i)\\\\
i_T^* & = arg\\max\\limits_{i}\\delta_T(i)
\\end{split}
\\]

    ④ Backtracking. For t=T-1,...,1
\\[
i_t^* = \\psi_{t+1}(i_t+1^*)
\\]

    Finally, we can get the optimal path $I^*=(i^*_1,i^*_2,...,i^*_T)$

Words in the end

    At the begining of the new term, I complete this eassy eventually. The purpose that I write this $‘Hidden\\quad Markov\\quad Model‘$ is to have an understanding of HMM and practice my English writing skill, which is kind of disfluency...I‘m sorry :( ...

    The are also some quension after I complete this eassy:

    ① The relationship between HMM and PGM(Probabilistic Graphical Model). There are some probability calculation in forward algorithm and backward algorithm and they are quite related to PGM.

    ② In Baum-Welch algorithm, how to use Lagrange method to find the solution?

    ③ In HMM learning problem, how to deal with multiple sequence when trainning the model?

 

Reference

[1] 李航.统计学习方法[M].北京:清华大学出版社.

[2] LAWRENCE R. RABINER.A Tutorial on Hidden Markov Models and
Selected Applications in Speech Recognition[J].PROCEEDINGS OF THE IEEE,FEBRUARY 1989

[3] 刘成林.中国科学院大学《模式识别》PPT