[NOI2013]快餐店

Posted 2020-08-31 神犇(shenben)

题目描述

小T打算在城市C开设一家外送快餐店。送餐到某一个地点的时间与外卖店到该地点之间最短路径长度是成正比的，小T希望快餐店的地址选在离最远的顾客距离最近的地方。

快餐店的顾客分布在城市C的N 个建筑中，这N 个建筑通过恰好N 条双向道路连接起来，不存在任何两条道路连接了相同的两个建筑。任意两个建筑之间至少存在一条由双向道路连接而成的路径。小T的快餐店可以开设在任一建筑中，也可以开设在任意一条道路的某个位置上（该位置与道路两端的建筑的距离不一定是整数）。

现给定城市C的地图（道路分布及其长度），请找出最佳的快餐店选址，输出其与最远的顾客之间的距离。

输入输出格式

输入格式：

 

输入文件foodshop.in第一行包含一个整数N，表示城市C中的建筑和道路数目。

接下来N行，每行3个整数，Ai，Bi，Li（1≤i≤N；Li>0），表示一条道路连接了建筑Ai与Bi，其长度为Li 。

 

输出格式：

 

输出文件foodshop.out仅包含一个实数，四舍五入保留恰好一位小数，表示最佳快餐店选址距离最远用户的距离。

注意：你的结果必须恰好有一位小数，小数位数不正确不得分。

 

输入输出样例

输入样例#1：

【样例输入1】
4 
1 2 1 
1 4 2 
1 3 2 
2 4 1
【样例输入2】
5
1 5 100
2 1 77
3 2 80
4 1 64
5 3 41

输出样例#1：

【样例输出1】
2.0 
【样例输出2】
109.0

说明

样例1

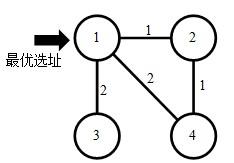
样例2

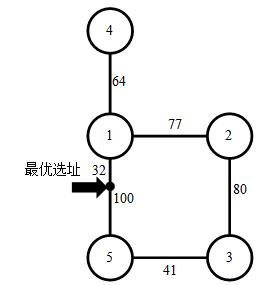
数据范围

对于 10%的数据，N<=80,Li=1；

对于 30%的数据，N<=600，Li<=100；

对于 60% 的数据，N<=2000，Li<=10^9；

对于 100% 的数据，N<=10^5，Li<=10^9

 

/*
60分是非常好写的，
    因为这个图里有且仅有一个环，因此这个环上肯定有一条边是不走的。
    因此直接枚举这条边，剩下的就是一棵树了，
    显然应该建在树的重心上，答案就是D/2，其中D表示剩下的树的直径。
在这些答案中取个最小值，就可以了。
因为抽环比较麻烦，所以直接全部枚举，
再检查一下剩下的树中是否还有环以及是否连通就可以了
*/
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
typedef long long ll;

#define FRE(name) freopen(#name".in","r",stdin);freopen(#name".out","w",stdout);
#define fre(name) freopen(#name".txt","r",stdin);
#define fi first
#define se second
#define m(s) memset(s,0,sizeof s);
#define debug(x) cout<<#x<<" "<<x<<\'\\n\'; 
#ifdef WIN32
#define LL "%I64d"
#else
#define lL "%lld"
#endif

const int N=1e5+5;
const ll mod=1e9+7;
struct nedge{int v,next;ll w;}e[N<<1];int tot,head[N];
pair<int,int>Q[N];bool vis[N];
int n,la,lb,id,flag;ll mx;
inline int read(){
    int x=0;char ch=getchar();
    while(ch<\'0\'||ch>\'9\'){ch=getchar();}
    while(ch>=\'0\'&&ch<=\'9\'){x=x*10+ch-\'0\';ch=getchar();}
    return x;
}
inline void add(int x,int y,int z){
    e[++tot].v=y;e[tot].w=z;e[tot].next=head[x];head[x]=tot;
    e[++tot].v=x;e[tot].w=z;e[tot].next=head[y];head[y]=tot;
}
inline void init(){
    n=read();
    for(int i=1,x,y,z;i<=n;i++){
        Q[i].fi=read();Q[i].se=read();z=read();
        add(Q[i].fi,Q[i].se,z);
    }
}
void dfs(int x,int f,ll d){
    if(d>mx) mx=d,id=x;
    if(vis[x]){
        flag=0;
        return ;
    }
    vis[x]=1;
    for(int i=head[x];i;i=e[i].next){
        int v=e[i].v;
        if(x==la&&v==lb) continue;
        if(x==lb&&v==la) continue;
        if(v==f) continue;
        dfs(v,x,d+e[i].w);
    }
}
inline void work(){
    double ans=-1;
    for(int i=1;i<=n;i++){
        la=Q[i].fi;lb=Q[i].se;
        flag=1;
        m(vis);mx=-1;dfs(la,0,0);
        for(int j=1;j<=n;j++) if(!vis[j]){flag=0;break;}
        if(!flag) continue;
        m(vis);mx=-1;dfs(id,0,0);
        if(ans==-1||mx/2.0<ans) ans=mx/2.0;
    }
    printf("%.1lf",ans);
}
int main(){
    FRE(foodshop);
    init();
    work();
    return 0;
}

暴力60分代码

【前言】：

m=n,基环外向树(章鱼图)

【分析】：

对于暴力TLE的原因是每一次枚举边都要dfs一遍。O(n^2)

于是我们断环成链，dp。

讨论：

1.最长链不经过环

2、最长链经过环

 

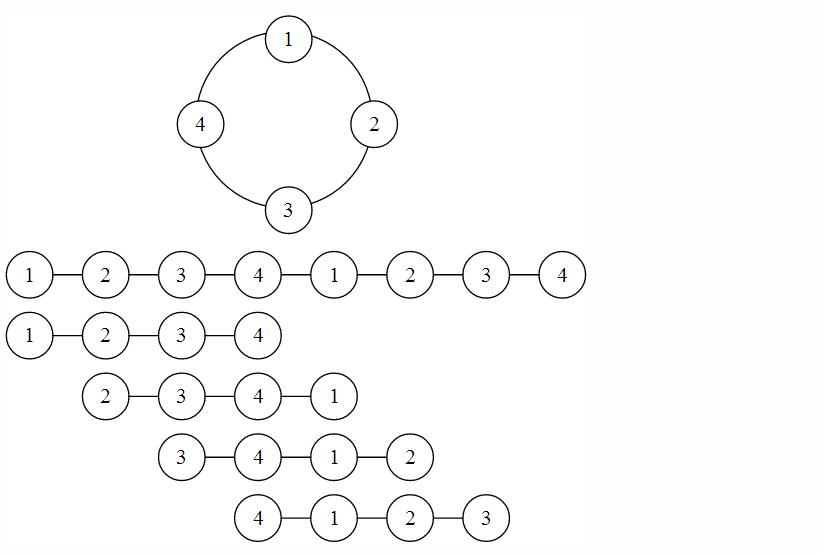
#include<cstdio>
#include<iostream>
#define setfire(name) freopen(#name".in","r",stdin);freopen(#name".out","w",stdout);
using namespace std;
typedef long long ll;

const int N=1e5+5,M=N<<1;
int n,dfs_cnt,top,dfn[N],pre[N],stack[N];bool ring[N];
int tot,to[M],nxt[M],head[N];ll val[M];
ll ans,sum,Mx,b[N],c[N],u1[N],u2[N],v1[N],v2[N],dis[N];

void add(int x,int y,int z){
    to[++tot]=y;val[tot]=z;nxt[tot]=head[x];head[x]=tot;
    to[++tot]=x;val[tot]=z;nxt[tot]=head[y];head[y]=tot;
}
void dfs_circle(int x){
    dfn[x]=++dfs_cnt;
    for(int i=head[x],y;i;i=nxt[i]){
        if((y=to[i])!=pre[x]){
            if(!dfn[y]){
                pre[y]=x;
                c[y]=val[i];
                dfs_circle(y);
            }
            else if(dfn[y]>dfn[x]){
                for(;x!=y;y=pre[y]){
                    stack[++top]=y;
                    b[top]=c[y];
                    ring[y]=true;
                }
                stack[++top]=x;
                b[top]=val[i];
                ring[x]=true;
                return ;
            }
        }
    }
}
void dp_tree_len(int x,int fa){
    for(int i=head[x],y;i;i=nxt[i]){
        if((y=to[i])!=fa&&!ring[y]){
            dp_tree_len(y,x);
            ans=max(ans,dis[x]+dis[y]+val[i]);
            dis[x]=max(dis[x],dis[y]+val[i]);
        }
    }
}
int main(){
    setfire(foodshop);
    scanf("%d",&n);
    for(int i=1,x,y,z;i<=n;i++){
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
    }
    dfs_circle(1);
    for(int i=1;i<=top;i++) dp_tree_len(stack[i],0);
    for(int i=1;i<=top;i++){
        sum+=b[i-1];
        u1[i]=max(u1[i-1],sum+dis[stack[i]]);
        v1[i]=max(v1[i-1],sum+dis[stack[i]]+Mx);
        Mx=max(Mx,dis[stack[i]]-sum);
    }
    ll tmp=b[top];Mx=sum=b[top]=0;
    for(int i=top;i>=1;i--){
        sum+=b[i];
        u2[i]=max(u2[i+1],sum+dis[stack[i]]);
        v2[i]=max(v2[i+1],sum+dis[stack[i]]+Mx);
        Mx=max(Mx,dis[stack[i]]-sum);
    }
    ll Mn=v1[top];
    for(int i=1;i<top;i++)
        Mn=min(Mn,max(max(v1[i],v2[i+1]),tmp+u1[i]+u2[i+1]));
    ans=max(ans,Mn);
    printf("%.1lf",ans/2.0);
    return 0;
}