求解单独像对相对定向元素(数字摄影测量中的解析法相对定向)
Posted yogurtWX
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了求解单独像对相对定向元素(数字摄影测量中的解析法相对定向)相关的知识,希望对你有一定的参考价值。
yogurt今天要和大家分享的是我自己在选修课数字摄影测量上学到的一点关于立体像对的解析法相对定向的知识,首先yogurt必须给大家梳理一下摄影测量几种解析方式的区别与联系,将这些关系梳理好了之后写程序的思路才会更清晰哦!
--------------------------------------------------------yogurt小课堂开课啦-----------------------------------------------------------
在摄影测量中,为了从获取的影像中确定被研究物体的位置、形状、大小及其相互关系,除了应用到双向立体测图法(模拟法、解析法及数字法)外,还可以利用物方和像方之间的解析关系式通过计算来获取(《摄影测量学》第五章前言)。涉及到坐标系统、内外方位元素以及共线条件方程式这三个大方面。其中最最重要的解析关系式非共线条件方程莫属!
(一)、坐标系统:
二维的框标坐标系x/y 、 像平面坐标系x/y ;
三维的像空间坐标系S-X/Y/Z 、 像空间辅助坐标系S-U/V/W 、 地面测量坐标系(左手系)T-Xt/Yt/Zt 、 地面摄影测量坐标系D-X/Y/Z 。
(二)、内外方位元素:
3个内方位元素:主距f、像主点在框标坐标系中的坐标x0、y0;
6个外方位元素:3个直线元素:摄影中心在地面空间坐标系中的坐标值Xs/Ys/Zs,通常选择的是地面摄影测量坐标系;
3个角元素:航向倾角、旁向倾角、像片旋角。
(三)、由共线条件方程在不同条件下应用求得关于摄影测量的信息如:
1、单像空间后方交会
已知:一张摄影像片的内方位元素x0/y0/F、摄影比例尺m、地面控制点的地面坐标(X/Y/Z)及其对应的像点像平面坐标(x/y),求解:该像片的六个外方位元素。
2、立体像对的前方交会
已知:一对立体像对中两张像片各自的内外方位元素和像点像平面坐标(x/y),求解:相应地面点的地面坐标(X/Y/Z)。
3、立体像对的解析法相对定向:
确定立体像对两张像片相对位置和姿态,建立一个与拍摄时相似的立体模型,以确定模型点的三维坐标。分为求解连续像对相对定向元素和求解单独像对相对定向元素两种:
(1)求解连续像对相对定向元素:以左像片为基础,求出右像片相对于左像片的五个相对定向元素(摄影中心在地面摄影测量坐标系中副轴和第三旋转轴方向上的坐标值V/W、航向倾角ψ、旁向倾角ω、像片旋角κ)
此时,左片外方位元素U1=V1=W1=ψ1=ω1=κ1=0;右片外方位元素中U2只涉及比例尺,V2、W2、ψ2、ω2、κ2未知;
(2)求解单独像对相对定向元素:以基线作为主轴,左主核面为uw平面,建立像空间辅助坐标系S1-U1/V1/W1及S2-U2V2W2,求出此时的五个相对定向元素(左像片的航向倾角ψ1、像片旋角κ1以及右像片的航向倾角ψ2、旁向倾角ω2、像片旋角κ2)
此时,左片外方位元素U1=V1=W1=0,ω1=0,剩下的ψ1、κ1未知;右片外方位元素U2=B(摄影基线)、V2=W=02,剩下的ψ2、ω2、κ2。
-----------------------------------------------------------------下课啦---------------------------------------------------------------
该程序涉及到的基础操作有读写文件、矩阵的乘法、转置和求逆。接下来让我们一起练习一下吧!
要求:根据某对立体像对中同名像点的左、右影像的行、列号数据,按单独像对相对定向方法,求解该立体像对的相对定向元素?
数据:类似这个样子就可以啦,这是我数据的一部分哈,第一排是像对数,剩下的每一排四个数据的前两个是左像片的某像元的行列数,后两个是右像片的相对像元的行列数:

已知:影像尺寸(像素):宽度 = 8000; 高度= 11500;像元尺寸0.009毫米,像片主距50.2毫米。像主点:行号(像素)5749、列号(像素)3999。
程序思路:那首先yogurt还是带着大家看一看程序思路吧~~
1、 读入数据并将行列号转换为X、Y坐标
1.1 从文件中读入立体像对中同名像点的左、右影像的行、列号数据,分别将左、右影像的数据存入left和right数组中(数组元素是Point,如:left[3].x表示第三对立体像对的同名像点在左影像上的列数;right[3].y表示第三对立体像对的同名像点在右影像上的行数;)。
1.2 利用像主点的行列号,将同名像点的行列号转换为XY坐标,计算公式如下:
x=(列数-COL像主点)*SIZE;
y=(ROW像主点-行数)*SIZE。
2、 求解左右影像像主点的像空辅坐标系下的坐标(u,v,w)
2.1 求旋转矩阵R[3][3],根绝旋转矩阵R的元素计算公式可以得到R矩阵,计算公式如下:
R2[0][0] = cos(ψ2)*cos(κ2) - sin(ψ2)*sin(ω2)*sin(κ2);
R2[0][1] = -cos(ψ2)*sin(κ2) - sin(ψ2)*sin(ω2)*cos(κ2);
R2[0][2] = -sin(ψ2)*cos(ω2);
R2[1][0] = cos(ω2)*sin(κ2);
R2[1][1] = cos(ω2)*cos(κ2);
R2[1][2] = -sin(ω2);
R2[2][0] = sin(ψ2)*cos(κ2) + cos(ψ2)*sin(ω2)*sin(κ2);
R2[2][1] = -sin(ψ2)*sin(κ2) + cos(ψ2)*sin(ω2)*cos(κ2);
R2[2][2] = cos(ψ2)*cos(ω2)。
2.1 利用旋转矩阵以及像平面坐标,利用矩阵乘法,得到像空辅坐标。
右像片的与左像片的像空辅坐标计算方法一样。
3、 计算误差方程式的系数和常数项
3.1 系数项计算公式我
A[i][0] = u1*v2 / w2;
A[i][1] = -u2*v1 / w1;
A[i][2] = F*(1 + v1*v2 / (w1*w2));
A[i][3] = -u1;
A[i][4] = u2。
3.2 常数项计算公式
L[i][0] = -F*v1 / w1 + F*v2 / w2。
4、 解算未知数
4.1 利用矩阵的乘法,矩阵转置以及矩阵求逆的函数(在主函数前已经声明且定义),计算改正数。
4.2 根据改正数更新未知数,并判断是否已经满足误差标准,即每个改正数的绝对值是否都小于0.3*0.0001。若满足则停止迭代,否则继续进行迭代,直到满足误差限制为止。
嘿嘿,你一定知道yogurt又要直接把平时写的作业中的代码粘上来炫耀了。

// test.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include<math.h> #include<stdlib.h> #define WIDTH 8000; #define HEIGHT 11500; #define SIZE 0.009; #define COL 3999 #define ROW 5749 #define F 50.2 #define NUM 63 #define NUM2 5 #define TOLERANCE 0.3*0.0001 #define Basic 24.223500 typedef struct POINT { double x, y; }point; void read(point *left, point *right, char *filename) { FILE * fp = fopen(filename, "r"); if (fp==NULL) { printf("ERROR"); return; } int num; fscanf(fp, "%d", &num); for (int i = 0; i < num; i++) { fscanf(fp, "%lf,%lf,%lf,%lf", &left[i].y, &left[i].x, &right[i].y, &right[i].x); } fclose(fp); return; } void matrixmultiply(double **R, double **A, double **B,int a,int b,int c) { double sum; for (int i = 0; i < a; i++) { for (int j = 0; j < c; j++) { sum = 0; for (int k = 0; k < b; k++) { sum += R[i][k] * A[k][j]; } B[i][j] = sum; } } return; } void matrixtran(double **A, double **AT) { for (int i = 0; i < NUM; i++) { for (int j = 0; j < NUM2; j++) { AT[j][i] = A[i][j]; } } return; } void matrixinverse(double **A, double **B) { double z[NUM2][NUM2*2],h; int i, j, m; //增广矩阵(A | E)存入二维数组z中 for (i = 0; i < NUM2; i++) for (j = 0; j < NUM2; j++) z[i][j] = A[i][j]; for (i = 0; i < NUM2; i++) for (j = NUM2; j < NUM2 * 2; j++) z[i][j] = 0; for (i = 0; i < NUM2; i++) z[i][i+NUM2] = 1; //调整扩展矩阵,若某一列全为0则不存在逆矩阵 for (i = 0; i < NUM2; i++)//行 { if (z[i][i] == 0)//某行对角线数值为0,需要调整 { for (j = 0; j < NUM2; j++)//行 { if (z[j][i] != 0)//第j行i列不为0,交换第i行和第j行 { for (m = 0; m < NUM2*2; m++)//列 { h = z[i][m]; z[i][m] = z[j][m]; z[j][m] = h; } break; }//交换完毕 } if (j > NUM2) printf("该列没有不为0的行,没有逆矩阵"); }//调整完毕 } //计算扩展矩阵 for (i =0; i < NUM2; i++)//行 { double first = z[i][i]; //使z[i][i]=1 for (j = 0; j < NUM2*2; j++)//列 { z[i][j] /= first; } //把其他行在该列的数值变为0 for (m = 0; m < NUM2; m++) { if (m == i)//遇到自己这行 continue; double beishu = z[m][i]; for (int n = 0; n < NUM2 * 2; n++)//转换m行的每一列,保证z[m][i]=0 { z[m][n] -= z[i][n] * beishu; } } } //取扩展矩阵后的NUM2*NUM2矩阵,放到B中 for (i = 0; i < NUM2; i++) { for (j = NUM2; j < NUM2 * 2; j++) { B[i][j - NUM2] = z[i][j]; } } } int _tmain(int argc, _TCHAR* argv[]) { /*同名像点行列号rows,cols-->像平面坐标x,y,像平面坐标结果输出到"coordinate.txt" */ //开辟数组left和right分别存储左右同名像点的行列号 point left[63], right[63]; //从txt文件中读入左右同名像点的行列号 read(left, right, "同名点左右影像行列号文件.txt"); //将行列号转换为坐标(公式:x=(c-COL)*SIZE,y=(ROW-h)*SIZE),并输出 double xleft[NUM], yleft[NUM], xright[NUM], yright[NUM]; FILE *fp = fopen("coordinate.txt", "w"); if (fp == NULL) { printf("ERROR"); return 0; } fprintf(fp, "%d\\n", NUM); for (int i = 0; i < NUM; i++) { //左影像 xleft[i] = (left[i].x - COL)*SIZE; yleft[i] = (ROW - left[i].y)*SIZE; //右影像 xright[i] = (right[i].x - COL)*SIZE; yright[i] = (ROW - right[i].y)*SIZE; //输出 fprintf(fp, "%d\\t%lf\\t%lf\\t%lf\\t%lf\\n", i, xleft[i], yleft[i], xright[i], yright[i]); } fclose(fp); /*第一次迭代的误差方程的系数矩阵A、常数矩阵L输出到"parameter matrix.txt" */ //设置待求的相对定向元素的初始值 double ψ1 = 0, ω1 = 0, κ1 = 0, ψ2 = 0, ω2 = 0, κ2 = 0; double u1, v1, w1, u2, v2, w2; //系数矩阵 double **A = (double **)malloc(sizeof(double*)*NUM);//NUM*NUM2矩阵 for (int w = 0; w < NUM; w++) { A[w] = (double *)malloc(sizeof(double)*NUM2); } //常数矩阵 double **L = (double **)malloc(sizeof(double*)*NUM);//NUM*1矩阵 for (int w = 0; w < NUM; w++) { L[w] = (double *)malloc(sizeof(double) * 1); } //改正数矩阵 double **X = (double **)malloc(sizeof(double*)*NUM2);//NUM2*1矩阵 for (int w = 0; w < NUM2; w++) { X[w] = (double *)malloc(sizeof(double) * 1); } int number = 0; //计算迭代次数 //定义旋转矩阵 double **R1 = (double **)malloc(sizeof(double*) * 3);//3*3矩阵 for (int w = 0; w < 3; w++) { R1[w] = (double *)malloc(sizeof(double) * 3); } double **R2 = (double **)malloc(sizeof(double*) * 3);//3*3矩阵 for (int w = 0; w < 3; w++) { R2[w] = (double *)malloc(sizeof(double) * 3); } //定义中间矩阵 double **AT = (double **)malloc(sizeof(double*)*NUM2);//NUM2*NUM矩阵 for (int w = 0; w < NUM2; w++) { AT[w] = (double *)malloc(sizeof(double) * NUM); } double **p1 = (double **)malloc(sizeof(double*)*NUM2);//NUM2*NUM2矩阵 for (int w = 0; w < NUM2; w++) { p1[w] = (double *)malloc(sizeof(double) * NUM2); } double **p2 = (double **)malloc(sizeof(double*)*NUM2);//NUM2*NUM2矩阵 for (int w = 0; w < NUM2; w++) { p2[w] = (double *)malloc(sizeof(double) * NUM2); } double **p3 = (double **)malloc(sizeof(double*)*NUM2);//NUM2*NUM矩阵 for (int w = 0; w < NUM2; w++) { p3[w] = (double *)malloc(sizeof(double) * NUM); } while (1) { //对于每一对同名像点 for (int i = 0; i < NUM; i++) { //计算像点的像空间辅助坐标(u1,v1,w1)和(u2,v2,w2),需要求旋转矩阵R1,R2 //求旋转矩阵R1,并计算u1,v1,w1 R1[0][0] = cos(ψ1)*cos(κ1) - sin(ψ1)*sin(ω1)*sin(κ1); R1[0][1] = -cos(ψ1)*sin(κ1) - sin(ψ1)*sin(ω1)*cos(κ1); R1[0][2] = -sin(ψ1)*cos(ω1); R1[1][0] = cos(ω1)*sin(κ1); R1[1][1] = cos(ω1)*cos(κ1); R1[1][2] = -sin(ω1); R1[2][0] = sin(ψ1)*cos(κ1) + cos(ψ1)*sin(ω1)*sin(κ1); R1[2][1] = -sin(ψ1)*sin(κ1) + cos(ψ1)*sin(ω1)*cos(κ1); R1[2][2] = cos(ψ1)*cos(ω1); double **M = (double **)malloc(sizeof(double*) * 3);//3*1矩阵 for (int w = 0; w < 3; w++) { M[w] = (double *)malloc(sizeof(double) * 1); } double **B = (double **)malloc(sizeof(double*) * 3);//3*1矩阵 for (int w = 0; w < 3; w++) { B[w] = (double *)malloc(sizeof(double) * 1); } M[0][0] = { xleft[i] }; M[1][0] = { yleft[i] }; M[2][0] = { -F }; matrixmultiply(R1, M, B, 3, 3, 1); u1 = B[0][0]; v1 = B[1][0]; w1 = B[2][0]; //求旋转矩阵R2,并计算u2,v2,w2 R2[0][0] = cos(ψ2)*cos(κ2) - sin(ψ2)*sin(ω2)*sin(κ2); R2[0][1] = -cos(ψ2)*sin(κ2) - sin(ψ2)*sin(ω2)*cos(κ2); R2[0][2] = -sin(ψ2)*cos(ω2); R2[1][0] = cos(ω2)*sin(κ2); R2[1][1] = cos(ω2)*cos(κ2); R2[1][2] = -sin(ω2); R2[2][0] = sin(ψ2)*cos(κ2) + cos(ψ2)*sin(ω2)*sin(κ2); R2[2][1] = -sin(ψ2)*sin(κ2) + cos(ψ2)*sin(ω2)*cos(κ2); R2[2][2] = cos(ψ2)*cos(ω2); double **C = (double **)malloc(sizeof(double*) * 3);//3*1矩阵 for (int w = 0; w < 3; w++) { C[w] = (double *)malloc(sizeof(double) * 1); } double **D = (double **)malloc(sizeof(double*) * 3);//3*1矩阵 for (int w = 0; w < 3; w++) { D[w] = (double *)malloc(sizeof(double) * 1); } C[0][0] = { xright[i] }; C[1][0] = { yright[i] }; C[2][0] = { -F }; matrixmultiply(R2, C, D, 3, 3, 1); u2 = D[0][0]; v2 = D[1][0]; w2 = D[2][0]; //逐点计算误差方程式的系数和常数 A[i][0] = u1*v2 / w2; A[i][1] = -u2*v1 / w1; A[i][2] = F*(1 + v1*v2 / (w1*w2)); A[i][3] = -u1; A[i][4] = u2; L[i][0] = -F*v1 / w1 + F*v2 / w2; } //解法方程,求改正数 //计算 matrixtran(A, AT); matrixmultiply(AT, A, p1, NUM2, NUM, NUM2); matrixinverse(p1, p2); matrixmultiply(p2, AT, p3, NUM2, NUM2, NUM); matrixmultiply(p3, L, X, NUM2, NUM, 1); //迭代结果:相对定向元素的改正数dψ1,dκ1和dψ2,dω2,dκ2 ψ1 += X[0][0]; ψ2 += X[1][0]; ω2 += X[2][0]; κ1 += X[3][0]; κ2 += X[4][0]; number++; //输出第一次迭代的系数矩A和常数矩阵L if (number == 1) { FILE *fp = fopen("parameter matrix.txt", "w"); if (fp == NULL) { printf("ERROR"); return 0; } fprintf(fp, "第一次的系数矩阵A:\\n"); for (int m = 0; m < NUM; m++) { for (int n = 0; n < 5; n++) { fprintf(fp, "%lf\\t", A[m][n]); } fprintf(fp, "\\n"); } fprintf(fp, "\\n第一次的常数矩阵L:\\n"); for (int m = 0; m < NUM; m++) { fprintf(fp, "%lf\\n", L[m][0]); } fclose(fp); } //判断迭代是否继续,设迭代终止阈值为0.3*pow(10,-4) int test = 0; for (int j = 0; j < 5; j++) { if (fabs(X[j][0]) < TOLERANCE) test++; } if (test == 5) { printf("左影像的相对定向旋转矩阵:\\n"); for (int row = 0; row < 3; row++) { for (int col = 0; col < 3; col++) { printf("%lf\\t", R1[row][col]); } printf("\\n"); } printf("右影像的相对定向旋转矩阵:\\n"); for (int row = 0; row < 3; row++) { for (int col = 0; col < 3; col++) { printf("%lf\\t", R2[row][col]); } printf("\\n"); } break; } } /*输出相对定向线元素*/ printf("\\n相对定向线元素:\\n"); printf("左:\\t0.000000\\t0.000000\\t0.000000"); printf("\\n右:\\t%lf\\t0.000000\\t0.000000",Basic); /*输出相对定向角元素*/ printf("\\n相对定向角元素:\\n"); printf("左:\\t%lf\\t%lf\\t%lf", ψ1, ω1, κ1); printf("\\n右:\\t%lf\\t%lf\\t%lf", ψ2, ω2, κ2); /*输出迭代阈值,迭代次数和5个相对定向元素的最终值 */ printf("\\n\\n迭代阈值:%lf\\n迭代次数:%d", TOLERANCE, number); }
那给大家看看最终结果以及参数在中间过程的变化情况,以便于程序有错误的宝宝们对照调试哦~~
1、 像对的行列号转换为像平面坐标:
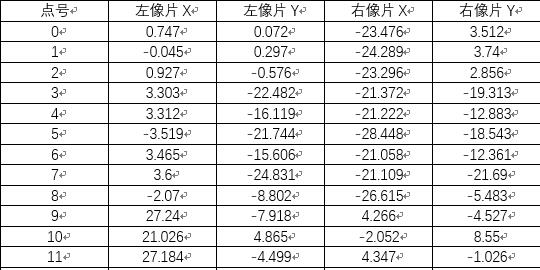
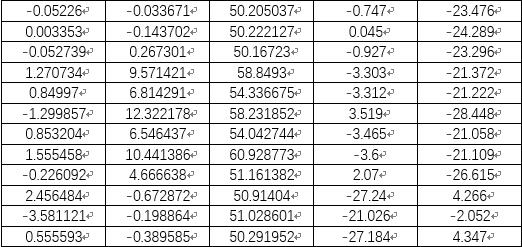
2、 第一次迭代时的误差方程的系数阵A、常数阵L:
(程序输出文件“parameter matrix.txt”,数据信息存储在txt文件中,可转为表格)
(1) 第一次的系数矩阵A
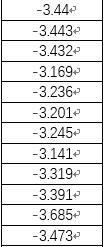
(2) 第一次的常数矩阵L
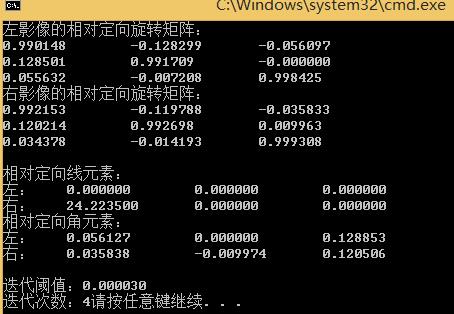
3、 控制台显示效果:
(如果数据不一样那最后计算出来的相对定向元素就会不一样哦)
以上是关于求解单独像对相对定向元素(数字摄影测量中的解析法相对定向)的主要内容,如果未能解决你的问题,请参考以下文章
数据结构与算法之深入解析“删除排序链表中的重复元素II”的求解思路与算法示例
数据结构与算法之深入解析“下一个更大元素II”的求解思路与算法示例
