算法导论 红黑树 实现

Posted 2020-08-31 itdef

学习算法 还是建议看看算法导论

算法导论第三版 如果不看数学推导 仅看伪代码 难度还是适中

本系列只是记录我的学习心得 和伪代码转化代码的过程

深入学习 还是建议大家看看算法书籍 教程更加系统。

本文参考算法导论第12章节 二叉树

代码由本人写成

转载请标明出处

 

 

首先

由于红黑树的删除用到了二叉树的一些函数 所以我们从二叉树讲起

二叉树 不带颜色的红黑树 看看两张画的有点丑的图

如图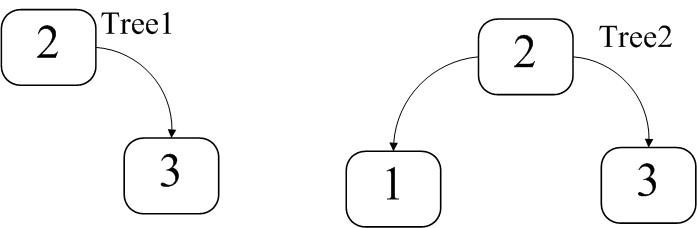

 

一个节点 记录一个数值 同时还有两个指向该节点两个儿子的标识

儿子有两个 左儿子和右儿子

图中就有两个二叉树示例

一个仅有右儿子  一个左右儿子均有

C语言中或者C++语言中我们这样定义二叉树结构

struct node {
	std::shared_ptr<node> left_;　　//智能指针
	std::shared_ptr<node> right_;
	int value_;
	node() {
		left_ = right_ = nullptr;
		value_ = -1;
	}
};

那么遍历树中的元素然后打印的代码如下

void PrintTree(const std::shared_ptr<node>& root) {
	if (root == nullptr)
		return;
	std::cout << root->value_ << " ";
	PrintTree(root->left_);
	PrintTree(root->right_);
}

　　

 我们现在创建一个图中TREE2并把它的元素数值依次打印出来

// 122.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <memory>
#include <iostream>

struct node {
	std::shared_ptr<node> left_;
	std::shared_ptr<node> right_;
	int value_;
	node() {
		left_ = right_ = nullptr;
		value_ = -1;
	}
};

void PrintTree(const std::shared_ptr<node>& root) {
	if (root == nullptr)
		return;
	std::cout << root->value_ << " ";
	PrintTree(root->left_);
	PrintTree(root->right_);
}


int main()
{
	std::shared_ptr<node> root(new node);
	root->value_ = 2;

	std::shared_ptr<node> x(new node);
	x->value_ = 1;
	root->left_ = x;

	std::shared_ptr<node> y(new node);
	y->value_ = 3;
	root->right_ = y;

	PrintTree(root);
	std::cout << std::endl;
    return 0;
}

　　打印结果如图:

 

树的最大值和最小值

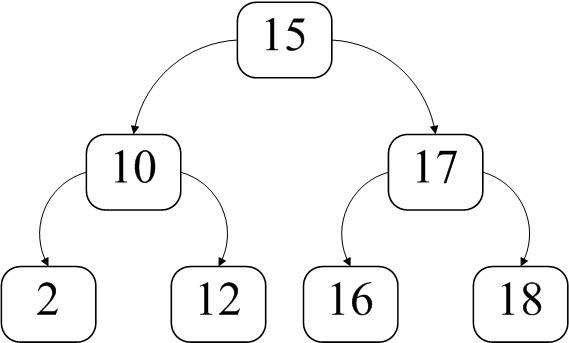
如果我们规定

节点的左儿子及左儿子的儿子(子孙)都比该节点小

节点的右儿子及右儿子的儿子(子孙)都比该节点小

那么获取该二叉树的最大最小值就很简单了

沿左儿子一直向下 获取最小值

沿右儿子一直向下 获取最大值

 

std::shared_ptr<node> TreeMinimum(std::shared_ptr<node> n) {
	while (n->left_ != nullptr) {
		n = n->left_;
	}
	return n;
}

std::shared_ptr<node> TreeMaximum(std::shared_ptr<node> n) {
	while (n->right_ != nullptr) {
		n = n->right_;
	}
	return n;
}

 

　　

 

 

// 122.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <memory>
#include <iostream>

struct node {
	std::shared_ptr<node> left_;
	std::shared_ptr<node> right_;
	int value_;
	node() {
		left_ = right_ = nullptr;
		value_ = -1;
	}
};

void PrintTree(const std::shared_ptr<node>& root) {
	if (root == nullptr)
		return;
	std::cout << root->value_ << " ";
	PrintTree(root->left_);
	PrintTree(root->right_);
}

std::shared_ptr<node> TreeMinimum(std::shared_ptr<node> n) {
	while (n->left_ != nullptr) {
		n = n->left_;
	}
	return n;
}

std::shared_ptr<node> TreeMaximum(std::shared_ptr<node> n) {
	while (n->right_ != nullptr) {
		n = n->right_;
	}
	return n;
}


int main()
{
	std::shared_ptr<node> root(new node);
	root->value_ = 15;
	std::shared_ptr<node> x = root;

	std::shared_ptr<node> n(new node);
	n->value_ = 10;
	x->left_ = n;
	x = n;

	n.reset(new node);
	n->value_ = 2;
	x->left_ = n;

	n.reset(new node);
	n->value_ = 12;
	x->right_ = n;

	x = root;
	n.reset(new node);
	n->value_ = 17;
	x->right_ = n;
	x = n;

	n.reset(new node);
	n->value_ = 16;
	x->left_ = n;

	n.reset(new node);
	n->value_ = 18;
	x->right_ = n;

	PrintTree(root);
	std::cout << std::endl;

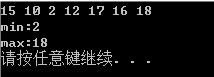
	std::cout << "min:" << TreeMinimum(root)->value_ << std::endl;
	std::cout << "max:" << TreeMaximum(root)->value_ << std::endl;
    return 0;
}

　　

 

 

后继和前驱 

讲了这么多 就是为了讲后继和前驱 二叉树和红黑树的删除用到了这个

该代码在后继红黑树章节中给出