NYOJ 164

Posted 2020-08-30

卡特兰数的一般项公式：

     　　

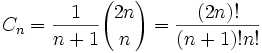
卡特兰数性质：

　　1.C_n的另一个表达形式为　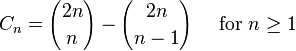　　　  所以，C_n是一个自然数，这一点在先前的通项公式中并不显而易见。

 

　　2.卡塔兰数满足以下递推关系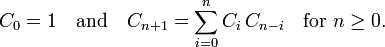：　　 ；   它也满足 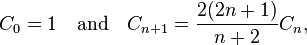，这提供了一个更快的计算卡特兰数的方法。

　　3.卡塔兰数的渐近增长为 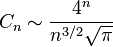   ， 它的含义是左式除以右式的商趋向于1 ，当n → ∞。(用斯特林公式易证。)

　　4.所有的奇卡塔兰数C_n(即Cn%2=1)都满足n = 2^k ? 1。

卡特兰数的应用：

　　1.括号化问题。

　　　　矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)

　　2.出栈次序问题。

　　　　一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
　　　　类似：
　　　　　　(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
　　　　　　(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。 即是NYOJ 164的题意。
　　3.将多边行划分为三角形问题。
　　　　将一个凸多边形区域分成三角形区域的方法数?
　　　　　　类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她
　　　　从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
　　　　　　类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
　　4.给顶节点组成二叉树的问题。
　　　　给定N个节点，能构成多少种形状不同的二叉树？
　　(一定是二叉树!先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) + ...+ h(n-1)h(0)=h(n) (能构成h(N)个)　

 

NYOJ 164实例：1. 用递推式写一个大数运算即可。

　　　　　　　　2.因为要求的数一共就100个，数据量太小，所以直接打表也行，比较白痴，但是可行。

 1 #include <cstdio>
 2 #include <cstring>
 3 int ans[102][100];
 4 
 5 void table(){
 6     ans[0][0] = ans[1][0] = 1;      //按照题意初始化 
 7     int i, j;
 8     for(i = 2; i < 102; i ++){        //计算2~102的结果  
 9         int c = 0;    
10         for(j = 0; j < 100; j ++){    //用h(n) = h(n-1)(4n-2)/(n+1)计算    
11             ans[i][j] = ans[i-1][j]*(4*i-2)+c;
12             c = ans[i][j]/10;
13             ans[i][j] %= 10;
14         }
15         int z = 0;
16         for(j = 99; j >= 0; j --){
17             z= z*10+ans[i][j];
18             ans[i][j] = z/(i+1);
19             z %= (i+1);
20         }
21     }
22 }
23 
24 int main(){
25     table();
26     int temp;
27     while(scanf("%d", &temp), temp != -1){
28         int i = 99;
29         while(ans[temp][i] == 0) i --;    //计算该数有多少位，从后往前推掉即可   
30         while(i >= 0) printf("%d", ans[temp][i]), i--;
31         printf("\\n");
32     }
33     return 0;
34 }

法1