《机器学习实战》读书笔记2：K-近邻(kNN)算法

Posted 2020-08-30 xietx1995

声明：文章是读书笔记，所以必然有大部分内容出自《机器学习实战》。外加个人的理解，另外修改了部分代码，并添加了注释

1、什么是K-近邻算法？

简单地说，k-近邻算法采用测量不同特征值之间距离的方法进行分类。不恰当但是形象地可以表述为近朱者赤，近墨者黑。它有如下特点：

• 优点：精度高、对异常值不敏感、无数据输入假定
• 缺点：计算复杂度高、空间复杂度高
• 适用数据范围：数值型和标称型

---

2、K-近邻算法的工作原理：

存在一个样本数据集合，也称作训练样本集，并且样本集中的每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的数据后，将这个没有标签的数据的每个特征与样本集中的数据对应的特征进行比较，然后算法提取样本中特征最相似的数据（最邻近）的分类标签。一般来说，我们只选择样本数据集中前 $k$ 个最相似的数据，这就是 $k$-近邻算法中 $k$ 的出处，通常 $k$ 是不大于 20 的整数。最后，选择 $k$ 个最相似数据中出现次数最多的类别，作为新数据的分类。

---

2.1 一个例子

例子出自《机器学习实战》，中文版第16页，英文版第19页

下面举一个书本上的例子来说明 $k$-近邻算法大概的工作原理：
我们想使用 $K$-近邻算法来分来爱情片和动作片。有人曾统计过很多电影的打斗镜头和接吻镜头，下图显示了 6 部电影的打斗镜头和接吻镜头数。假如有一部未看过的电影，如何确定它是爱情片还是动作片呢？（当然了，我们这里不考虑爱情动作片。邪恶的笑容）我们可以使用 kNN(k-nearest neighbors algorithm) 来解决这个问题。

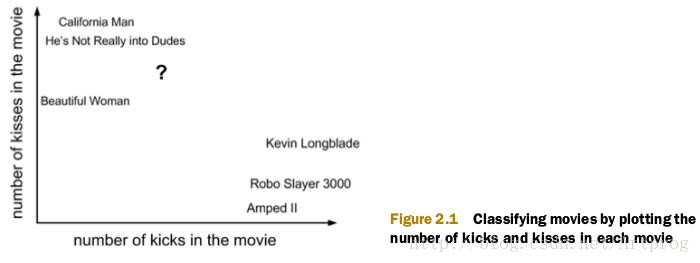
首先我们需要知道这个未知电影中存在多少个打斗镜头和接吻镜头，上图中问号的位置是该位置电影出现的镜头数的图形化展示，具体数字如下表所示：

电影名称	打斗镜头	接吻镜头	电影类型
California Man	3	104	爱情片
He’s Not Really into Dudes	2	100	爱情片
Beautiful Woman	1	81	爱情片
Kevin Longblade	101	10	动作片
Robo Slayer 3000	99	5	动作片
Amped II	98	2	动作片
?	18	90	未知

即使不知道未知电影属于哪种类型，我们也可以通过某种方法计算出来。首先要计算未知电影与样本集中其他电影的距离，计算方法很简单，即欧式空间距离(Euclidean Distance)，结果如下表所示。

电影名称	与未知电影的距离
California Man	20.5
He’s Not Really into Dudes	18.7
Beautiful Woman	19.2
Kevin Longblade	115.3
Robo Slayer 3000	117.4
Amped II	118.9

现在我们得到了样本集中所有电影与未知电影的距离，按照距离递增排序，可以找到 $k$ 个距离最近的电影，例如 $k=3$，则三个最靠近的电影是 He’s Not Really into Dudes、Beautiful Woman 和 California Man。$K$-近邻算法按照距离最近的三部电影的类型，决定未知电影的类型，而这三部电影全是爱情片，因此我们判定未知电影是爱情片。

---

2.2 K-近邻算法的一般流程

$k$-近邻算法的一般流程分为如下 6 个步骤：

1. 搜集数据：可以使用任何方法。
2. 准备数据：距离计算所需要的值，最好是结构化的数据。
3. 分析数据：可以使用任何方法。
4. 训练算法：此步骤不适用于$k$-近邻算法。
5. 测试算法：计算错误率。
6. 使用算法：首先需要输入样本数据和待分类数据，然后运行$k$-近邻算法判定待分类数据分别属于哪个分类，最后应用计算出的分类执行后续的处理。

---

3、使用python实现kNN算法

我们主要用的编程语言是python，以及一些python增强包。选用python使我们不许要考虑太多的编程细节，能够把重心都放在程序逻辑上。

---

3.1 使用python导入数据

机器学习最重要的就是数据，首先我们来捏造一些样本数据。将下面的代码保存到名为 kNN.py 的文本文件中：

from numpy import *

def createDataSet():
    dataSet = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # 创建一个2x2的数组
    labels = ['A', 'A', 'B', 'B'] # 创建一个长度为4的列表
    return dataSet, labels

在上面的代码中，我们导入了科学计算包 NumPy，如果你还没有安装 NumPy，请参考我的另外一篇文章《机器学习实战》读书笔记1：NumPy的安装及简单用法。

在上面的代码中，我们创建了一个大小为 2x2 的 NumPy 数组 dataSet，dataSet 的每一行是一个数据项。我们还创建了一个长度为 4 的列表 labels，labels 的每一项对应于 dataSet 的每一行，其对应关系如下表所示：

dataSet[i]，即样本	特征0	特征1	labels[i]，即样本对应的类别
dataSet[0]	1.0	1.1	A
dataSet[1]	1.0	1.0	A
dataSet[2]	0	0	B
dataSet[3]	0	0.1	B

现在我们打开命令提示符（我使用的是 Ubuntu），检查代码是否能够正常工作：
1. 在代码文件 kNN.py 所在目录下打开命令提示符（终端）
2. 在终端中输入python打开python（我使用的是python2.7）
3. 导入我们刚才写的代码 kNN.py：import kNN
4. 输入如下命令获得由函数 createDataSet() 捏造的数据样本并保存到变量 gropu 和 labels 中：
>>> group, labels = kNN.createDataSet()
5. 输入 group 和 labels 产看数据内容是否正确：
结果应该如下所示：

>>> group
array([[ 1. ,  1.1],
       [ 1. ,  1. ],
       [ 0. ,  0. ],
       [ 0. ,  0.1]])`
>>> labels
['A', 'A', 'B', 'B']

上述步骤的运行截图：

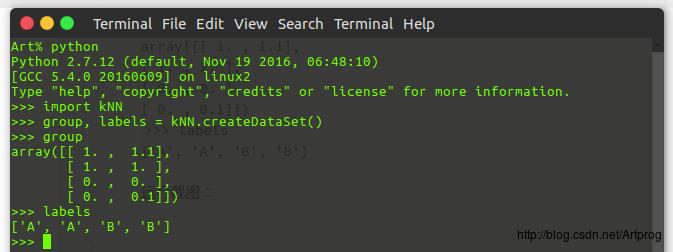
上面的四组数据和其对应的标签可以表示在如下的二维坐标系中：

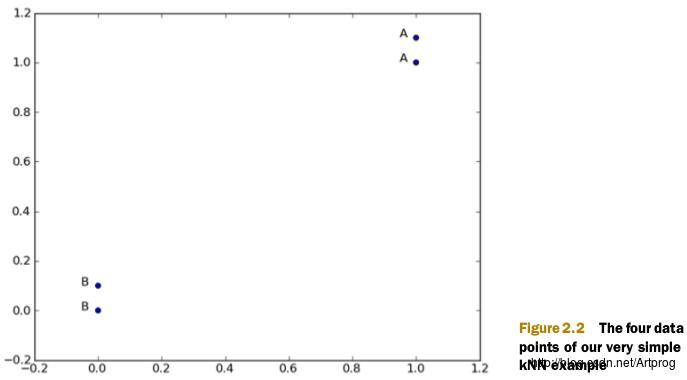
现在我们已经知道 python 如何解析数据，如何加载数据，以及 kNN 算法的工作原理，接下来我们将使用这些方法完成分类任务。

---

3.2 实施 kNN 算法

首先给出 kNN 算法的伪代码。对未知类别属性的数据集中的每个点一次执行以下操作：

1. 计算已知类别数据集中的每个点与未知点的距离；
2. 按照距离递增次序排序；
3. 选取与未知点距离最小的 k 个点；
4. 确定前 k 个点所在类别的出现频率；
5. 返回前 k 个点出现频率最高的类别作为未知点的预测分类。

下面我们写一个函数 classify0() 来实现上面的步骤：

from operator import itemgetter
# inVec为待分类向量，dataSet和labels为数据集，k是最近点的个数
def classify0(inVec, dataSet, labels, k):
    numberOfLines = dataSet.shape[0] # 获得数据集样本数量

    diffMat = tile(inVec, (numberOfLines, 1)) - dataSet # 将数据集中每个点都与待分类点相减，即各个特征相减
    squareDiffMat = diffMat**2 # 求差的平方
    squareDistance = squareDiffMat.sum(axis=1) # 求差的平方的和
    distances = squareDistance**0.5 # 对平方和开方得到距离

    # 对距离进行排序，argsort()函数默认按升序排列，但只返回下标，不对原数组排序
    sortedDistIndicies = distances.argsort()
    classCount = {} # 用于保存各个类别出现的次数

    for i in range(k): # 统计最近的 k 个点的类别出现的次数
        label = labels[sortedDistIndicies[i]]
        classCount[label] = classCount.get(label, 0) + 1

    # 对类别出现的次数进行排序，sorted()函数默认升序
    sortedClassCount = sorted(classCount.iteritems(), key=itemgetter(1), reverse=True)
    return sortedClassCount[0][0] # 返回类别出现次数最多的分类名称

相信上面代码的注释已经把代码解释的很清楚了。只需要注意以下几个函数和 numpy 语法的用法：
1、shape()函数：返回数组的尺寸信息，例如：

>>> x = tile((1,2),(3,2))
>>> x.shape[0] # 返回第0维的大小，行数
3
>>> x.shape[1] # 返回第1维的大小，列数
4
>>> shape(x) # 返回尺寸
(3, 4)

2、tile()函数：将数组、列表或元组平铺，返回平铺后的数组，例如 tile([1,2],(3,2)) 将返回如下数组：

>>> tile([1,2],(3,2)) 
array([[1, 2, 1, 2],
       [1, 2, 1, 2],
       [1, 2, 1, 2]])

3、sum()函数，示例：

>>> x = tile((1,2),(3,2))
>>> x
array([[1, 2, 1, 2],
       [1, 2, 1, 2],
       [1, 2, 1, 2]])
>>> x.sum(axis=0)
array([3, 6, 3, 6])
>>> x.sum(axis=1)
array([6, 6, 6])

4、argsort()函数，返回排序后的原来位置的索引。示例：

>>> v = [1, 4, 2, 3]
>>> argsort(v)
array([0, 2, 3, 1])

5、sorted()函数，按参数 key 排序，示例（按字典的键的值降序排列）：

>>> d = {'a':2,'b':1,'c':6,'d':-2}
>>> d
{'a': 2, 'c': 6, 'b': 1, 'd': -2}
>>> from operator import itemgetter
>>> sorted(d.iteritems(),key=itemgetter(1),reverse=True)
[('c', 6), ('a', 2), ('b', 1), ('d', -2)]

具体用法，请参考文档，或百度。

---

另外，我们在前面提到过，距离计算使用的是欧式距离，其公式如下：

d=(x0−x1)2+(y0−y1)2−−−−−−−−−−−−−−−−−−−√

以上是关于《机器学习实战》读书笔记2：K-近邻(kNN)算法的主要内容，如果未能解决你的问题，请参考以下文章

监督学习算法_k-近邻(kNN)分类算法_源代码

机器学习实战第2章 K-近邻算法(k-NearestNeighbor，KNN)

机器学习实战☛k-近邻算法（K-Nearest Neighbor， KNN）

机器学习实战☛k-近邻算法（K-Nearest Neighbor， KNN）

机器学习实战 k-近邻算法 实施kNN分类算法

机器学习实战 Task1 （KNN）k近邻算法的应用