机器为什么可以学习----vc维

Posted 2020-08-29 罐装可乐

1、主要内容

　　上节课讲述了vc bound，表明了在去break point为最小的break point时，m_H(N)的上限是vc bound是一个多项式级别的上限；

　　

　　vc维定义为当输入数据为N个点时，有一个假设空间H可以准确无误的将这N个点所有的分类情况都覆盖，那么假设空间的H的vc维就是N，当一个假设空间H维有限（霍夫丁不等式的上限的参数m_H(N)为有限的，因此bad的概率就会变得很小）时，当数据输入量够大（即霍夫丁不等式中的参数N，当N越大时，霍夫丁的上限就越小）时，学习就是可能的。

 

2、vc 维的定义

　　当成长函数m_H(N)存在break point时，其上限会被一个bound function所限制，同时这个bound function是一个多项式：

　　

　　因此，在成长函数存在break point同时输入数据规模N很大时，Ein ≈ Eout在很大的概率上都是正确的，保证了经训练数据训练得出的模型可以使用在测试数据上。

　　经过两组数据可知：

　　

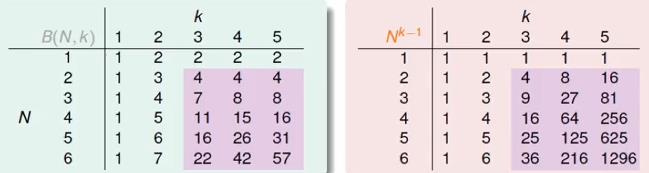
　　在N很大的情况下B(N,k) << N^k-1，因此有：

　　

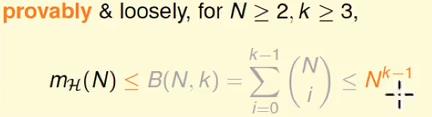
　　当vc bound存在时，对于hypothesis set中的任意一个hypothesis来说，霍夫丁不等式都是成立的也就是：

　　

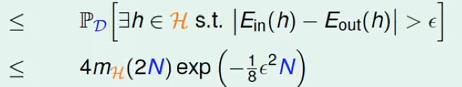
　　如果将成长函数mH(N)换成vc bound的上限，那么上述不等式可以写成：

　　

　　因此，根据某演算法从hypothesis set中选择的函数 g 必然也满足上式：

　　

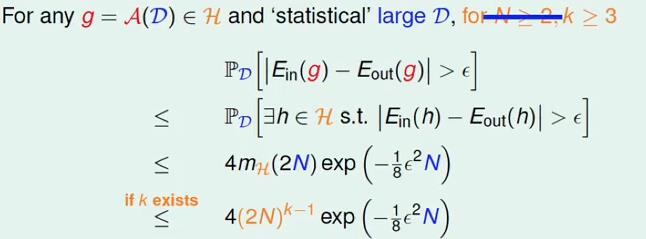
　　上式成立的前提条件为：

　　(1) 成长函数存在break point

　　(2) 训练数据量够大

　　

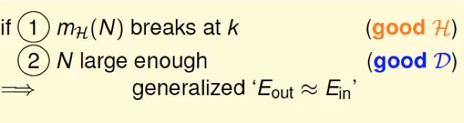
　　如果存在一个好的算法可以从hypothesis set中挑选出一个Ein最小的函数 g 那么学习的确是可行的。

　　

　　到目前，学习可行性的有了一定的理论支撑，此时的情况都是理想的情况，包括理想的hypothesis set（成长函数存在break point），理想的数据规模（够大）， 理想的演算法，实际情况以上都不能决定保证，只是大概率的情况下可以保证，因此可以说大概做到学习。

　　那么vc 维什么定义？vc 维与break point紧密联系：

　　

　　也就是说，vc维表示的hypothesis set 可以覆盖到数据规模中每一个特征的取值的情况的最大值，也就是break point的前面一个：

　　

　　当输入数据规模小于vc 维时，表示hypothesis set 可以全部覆盖到某些数据集，此时考虑的时不同的数据集整体的关系。

　　当数据输入规模大于vc 维时，表示此时的输入数据的规模N就是一个break point，因为vc 维决定了可以shatter的最大值，大于vc维的都是break point；

　　

　　因此上节课中成长函数的vc bound 可以写作：

　　

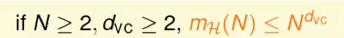
　　d_vc = k - 1；

　　几种vc 维：

　　

　　因此一个好的hypothesis set就是其vc 维有限；

　　vc维对于学习来说有什么好处？两者有什么联系？

　　vc 维有限可以保证Ein和Eout 在训练数据和测试数据上很接近，同时：

　　(1)不考虑算法的影响，无论演算法选择的hypothesis 是好还是坏，vc维有限都可以保证Ein和Eout很接近；

　　(2)之前的讨论中只是说输入数据是符合同一分布的，但是并不指定特定的分布，

　　(3)不用考虑target 函数f，

　　在以上的条件下一个完整的学习流程如下：

　　

　　3 感知机模型的vc维

　　感知机模型的学习操作流程：

　　

　　(1)、线性可分的数据集的情况下

　　(2)、PLA算法可以收敛，可以选择出一个函数使得E_in很小或者为0

　　(3)、经过多次迭代选择后，可以找到目标函数。

　　感知机模型操作流程对应的理论流程：

　　

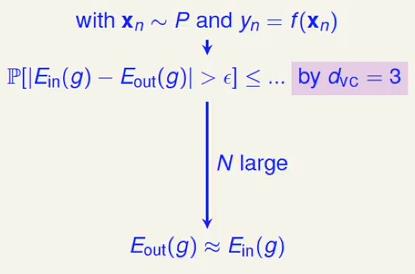
　　(1)、数据来源于同一分布，且目标函数存在

　　(2)、由于二维感知机模型的vc维为3，因此霍夫丁不等式成立，学习可行；

　　(3)、如果数据量够大，可以得出E_in ≈ E_out；

　　以上是二维感知机模型的学习流程，那么对于3维或者更高维的感知机模型，是否有同样的理论？

　　主要就是求解多维的感知机模型的vc维的值，已知的如下：

　　

　　经证明d维感知机模型的vc维的计算公式为 d_vc = d + 1。

 　　4、 vc维的物理意义

　　前面分析了d维感知机模型的vc维的计算公式：d_vc = d + 1，那么具体来说vc维的物理含义是什么？表示hypothesis set 参数w的自由度；

　　5、vc维结合霍夫丁不等式的使用

　　(1)、估算需要的数据量

　　(2)、计算模型的复杂度

　　

　　(3)、模型复杂度的推导：

　　在vc bound的霍夫丁不等式中表示的是发生坏事情的概率上限不超过一个以N为参数的值：该参数的值就是一般化的vc bound

　　

　　换个角度来说，坏事情的概率就是好的事情的反面，就是：

　　

　　引入参数σ表示不好的概率，那么就是：

　　

　　对σ进行反解可以得到ε的值：

　　

　　 反解出ε后带入到霍夫丁不等式中最终得到以下的表达式：表示E_in和E_out差距在反解的表达式内的概率是很大的。

 　　

　　以上的表达式成立的概率很大，成立的概率的下限是 1 - σ；

　　将上面的式子去掉绝对值符号：得出E_out被限制在一个范围之内，

　　

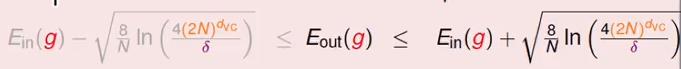
　　左侧灰色的部分我们不做考虑，因为Eout越小越好，对于右侧的部分来说表示E_out的上限值，也就是Eout的最坏的情况出现的概率，称其为模型的复杂度(hypothesis set的复杂度)，表示达到模型要求的性能所付出的努力。

　　

　　对于这个表达式，观察其特性：

　　对于dvc来说，当N一定是，其越大复杂度就越大；

　　对于Ein(g)来说，dvc越大，Ein就越小，这个因为当dvc越大表示其shatter的点就越多，shatter表示这个点可以有hypothesis set中的hypothesis set所覆盖，也就是hypothesis的一个点或者一部分，因此当dvc越大到无穷时，训练数据中的任何一个点都是hypothesis的一部分，那么Ein必然就为0了(个人理解)；

　　

　　从上面的图可以看出，最强大的hypothesis set不一定是最好的，越好的Ein表示hypothesis set的vc维就越高，同样带来的是hypothesis set或者模型的复杂度随之增高。

　　同样对于样本复杂度来说，就是对N进行求解，与上面的类似，不做详细求证；

　　理论上：

　　

　　实际上：

　　

　　这就是表示vc bound是比较宽松的：