Jacobi symbol(裸雅可比符号)
Posted 勿忘初心0924
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Jacobi symbol(裸雅可比符号)相关的知识,希望对你有一定的参考价值。
Jacobi symbol
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 625 Accepted Submission(s): 258
Problem Description
Consider a prime number p and an integer a !≡ 0 (mod p). Then a is called a quadratic residue mod p if there is an integer x such that x2 ≡ a (mod p), and a quadratic non residue otherwise. Lagrange introduced the following notation, called the Legendre symbol, L (a,p):
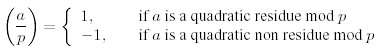
For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:
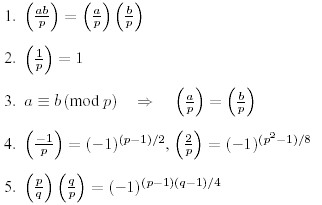
The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1. J (a, n) is only defined when n is an odd.
2. J (0, n) = 0.
3. If n is a prime number, J (a, n) = L(a, n).
4. If n is not a prime number, J (a, n) = J (a, p1) *J (a, p2)…* J (a, pm), p1…pm is the prime factor of n.
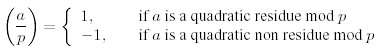
For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:
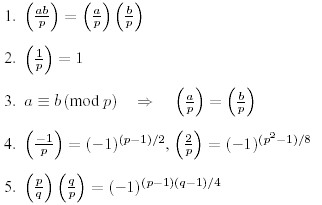
The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1. J (a, n) is only defined when n is an odd.
2. J (0, n) = 0.
3. If n is a prime number, J (a, n) = L(a, n).
4. If n is not a prime number, J (a, n) = J (a, p1) *J (a, p2)…* J (a, pm), p1…pm is the prime factor of n.
Input
Two integer a and n, 2 < a< =106,2 < n < =106,n is an odd number.
Output
Output J (a,n)
Sample Input
3 5
3 9
3 13
Sample Output
-1
0
1
Author
alpc41
Source
/* 题意:裸的雅可比符号,雅可比符号是勒让德符号的延伸,J(a,n)如果n是素数那么J(a,n)=L(a,n);否则J(a,n)=J(a,p1)*J(a,p2)*...J(a,pm); p1...pm是n的质因子,勒让德符号:定义为 L(a,n)=0 n mod a=0; L(a,n)=1 存在X使得 X^2 mod a=0; L(a,n)=-1 不存在X使得 X^2 mod a=0; #错误:求雅可比符号的时候,按照定义爆的,不知道哪里错了...分解质因子板套错了 #改进:勒让德符号n是偶数的时候要特判,特别要注意的时候质因子也有偶数,就是2 */ #include<bits/stdc++.h> #define ll long long using namespace std; /**********************勒让德符号************************/ ll exp(ll a,ll b,ll p) { ll res=1; for(;b;b>>=1) { if(b&1) res=(res*a)%p; a=(a*a)%p; } return res; } int cal(int a,int n) { if(a%n==0) return 0; else return exp(a,(n-1)/2,n)==1?1:-1; } /**********************勒让德符号************************/ /***********************筛素数*************************/ const int M = 1000100; int p[M], pNum=0; bool f[M]; void Prime() { int i, j; for(i = 2; i < 1000010; i++) { if(!f[i])//i是素数 { p[pNum++] = i; //将素数打到数组中 } for(j = 0; j < pNum && p[j] * i < M; j++ ) //将i的倍数都调出来因为,素数的倍数肯定不是素数 { f[p[j]*i] = 1; if(!(i%p[j])) break; } } } /***********************筛素数*************************/ int a,n; int cur; int main(){ Prime(); // freopen("in.txt","r",stdin); while(scanf("%d%d",&a,&n)!=EOF){ if(f[n]==0){//如果n是素数 printf("%d\n",cal(a,n)); continue; } cur=1; for(int i=0;n!=1&&i<pNum;i++){ if(n%p[i]==0){//这个是质因子 int total=0; while(n%p[i]==0){ total++; n/=p[i]; } int tmp=cal(a,p[i]); if(total%2==0&&tmp==-1)//如果n里面有偶数个的p,那么p乘偶数肯定不是奇数,就不符合勒让德符号定义了 tmp=1; cur*=tmp; } } printf("%d\n",cur); } return 0; }
以上是关于Jacobi symbol(裸雅可比符号)的主要内容,如果未能解决你的问题,请参考以下文章