UVa 1606 两亲性分子

Posted 2020-08-29 谦谦君子，陌上其华

https://vjudge.net/problem/UVA-1606

题意：平面上有n个点，每个点为白点或者黑点。现在需放置一条隔板，使得隔板一侧的白点数加上另一侧的黑点数总数最大。隔板上的点可以看做是在任意一侧。

思路：每次可以选取两个点作为隔板，所以我们可以先枚举一个基准点，然后算出其他点关于基准点的相对坐标和关于坐标系的极角（可以用atan2函数来计算，返回与x坐标值的角度），剩下的点依次与基准点形成分隔线，然后将一条直线绕基准点旋转，每当直线扫过一个点，就可以动态修改两侧的点数。

        本题还有一个优化的方法，那就是如果该点是黑点，就可以将它的坐标关于基准点旋转180°，这样扫描时就只需要计算一侧的白点数了。

        动态维护的情况如下：

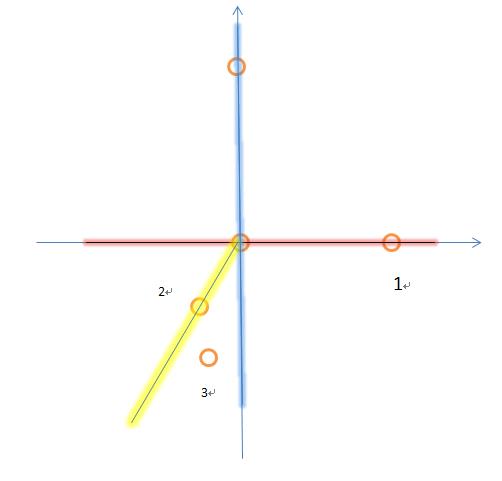
    首先，红色的为分割线，扫描线从红线开始逆时针扫描,当扫描线逆时针旋转至黄线时，由于旋转角度已大于180°，所以点数为3个。此时需要移动分隔线，即分隔线变为了蓝线，由于分隔线改变，原来的1号点到了分隔线的右边，此时总的点数需要减去1。此时扫描线与分隔线小于180°，所以扫描线还可以继续逆时针旋转直到y负轴，由于经过了2,3两点，总的点数需要加上2。此时总点数为4。之后分隔线继续旋转，重复上述步骤，直到所有分隔线都模拟完毕。

 1 #include<iostream>  
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cmath>
 5 using namespace std;
 6 
 7 const int maxn = 1000+5;
 8 
 9 int n;
10 int ans;
11 
12 struct node
13 {
14     int x, y;
15     int color;
16     double rad;
17     bool operator < (const node&rhs) const
18     {
19         return rad < rhs.rad;
20     }
21 }op[maxn],p[maxn];
22 
23 
24 bool left(node a, node b)
25 {
26     return a.x*b.y - a.y*b.x >= 0;
27 }
28 
29 void solve()
30 {
31     if (n <= 3)  { ans = n; return; }
32     ans = 0;
33     for (int i = 0; i < n; i++)  //枚举选择基点,一共有n个基点可以选择
34     {
35         int k = 0;
36         for (int j = 0; j < n; j++)    //计算出各个点关于基点的相对坐标
37         {
38             if (i == j)  continue;
39             p[k].x = op[j].x - op[i].x;
40             p[k].y = op[j].y - op[i].y;
41             if (op[j].color)    //如果为黑点，则可以将它旋转180之后变为白点来计数
42             {
43                 p[k].x = -p[k].x; p[k].y = -p[k].y;
44             }
45             p[k].rad = atan2(p[k].y, p[k].x);   //求极角,返回角度值
46             k++;
47         }
48         sort(p, p + k);
49         //基准点-p[L]为分割线，基准点-p[R]为扫描线
50         int    L = 0, R = 0, cnt = 2;   //初始点数设为2，即分隔线上的两个点
51         while (L < k)   //每个点都尝试与基点成为分割线
52         {
53             if (R == L)  { R = (R + 1) % k; cnt++; }  //空区域，数量+1，后面还会减去的
54             while (R != L && left(p[L], p[R]))   //R不等于L并且在180度之内
55             {
56                 R = (R + 1) % k;
57                 cnt++;
58             }
59             cnt--; //分隔线旋转，原本在分隔线上的点到了右边，所以要减去
60             L++;  //分隔线旋转
61             ans = max(ans, cnt);
62         }
63     }
64 }
65 
66 int main()
67 {
68     //freopen("D:\\\\txt.txt", "r", stdin);
69     while (cin >> n && n)
70     {
71         for (int i = 0; i < n; i++)
72             cin >> op[i].x >> op[i].y >> op[i].color;
73         solve();
74         cout << ans << endl;
75     }
76     return 0;
77 }