POJ3155 Hard Life [最大密度子图]

Posted 2020-08-29 Candy?

Hard Life

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 8646		Accepted: 2514
Case Time Limit: 2000MS		Special Judge

Description

John is a Chief Executive Officer at a privately owned medium size company. The owner of the company has decided to make his son Scott a manager in the company. John fears that the owner will ultimately give CEO position to Scott if he does well on his new manager position, so he decided to make Scott’s life as hard as possible by carefully selecting the team he is going to manage in the company.

John knows which pairs of his people work poorly in the same team. John introduced a hardness factor of a team — it is a number of pairs of people from this team who work poorly in the same team divided by the total number of people in the team. The larger is the hardness factor, the harder is this team to manage. John wants to find a group of people in the company that are hardest to manage and make it Scott’s team. Please, help him.

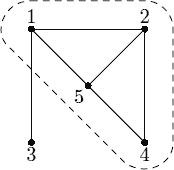
In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5 pairs work poorly in the same team, thus hardness factor is equal to ⁵⁄₄. If we add person number 3 to the team then hardness factor decreases to ⁶⁄₅.

Input

The first line of the input file contains two integer numbers n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 1000). Here n is a total number of people in the company (people are numbered from 1 to n), and m is the number of pairs of people who work poorly in the same team. Next m lines describe those pairs with two integer numbers a_i and b_i (1 ≤ a_i, b_i ≤ n, a_i ≠ b_i) on a line. The order of people in a pair is arbitrary and no pair is listed twice.

Output

Write to the output file an integer number k (1 ≤ k ≤ n) — the number of people in the hardest team, followed by k lines listing people from this team in ascending order. If there are multiple teams with the same hardness factor then write any one.

Sample Input

sample input #1
5 6
1 5
5 4
4 2
2 5
1 2
3 1

sample input #2
4 0

Sample Output

sample output #1
4
1
2
4
5

sample output #2
1
1

Hint

Note, that in the last example any team has hardness factor of zero, and any non-empty list of people is a valid answer.

Source

Northeastern Europe 2006

---

看论文去吧http://wenku.baidu.com/view/6b4baf1ffc4ffe473368ab25.html?re=view

思路就是01分数规划+最大权闭合子图

此题精度太恶心了，二分你还要用个ans来保存，然后l和r还要+-eps

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1105,M=4005,INF=1e9;
const double eps=1e-6;
inline int read(){
    char c=getchar();int x=0,f=1;
    while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1; c=getchar();}
    while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘; c=getchar();}
    return x*f;
}
int n,m,u[N],v[N],s,t;
struct edge{
    int v,ne;
    double c,f;
}e[M<<1];
int cnt,h[N];
inline void ins(int u,int v,double c){
    cnt++;
    e[cnt].v=v;e[cnt].c=c;e[cnt].f=0;e[cnt].ne=h[u];h[u]=cnt;
    cnt++;
    e[cnt].v=u;e[cnt].c=0;e[cnt].f=0;e[cnt].ne=h[v];h[v]=cnt;
}
int cur[N],d[N],vis[N];
int q[N],head,tail;
bool bfs(){
    head=tail=1;
    memset(vis,0,sizeof(vis));
    d[s]=1;vis[s]=1;q[tail++]=s;
    while(head!=tail){
        int u=q[head++];
        for(int i=h[u];i;i=e[i].ne){
            int v=e[i].v;
            if(!vis[v]&&e[i].c>e[i].f){
                vis[v]=1;d[v]=d[u]+1;
                q[tail++]=v;
                if(v==t) return true;
            }
        }
    }
    return false;
}
double dfs(int u,double a){
    if(u==t||a==0) return a;
    double flow=0,f;
    for(int &i=cur[u];i;i=e[i].ne){
        int v=e[i].v;
        if(d[v]==d[u]+1&&(f=dfs(v,min(e[i].c-e[i].f,a)))>0){
            flow+=f;
            e[i].f+=f;
            e[((i-1)^1)+1].f-=f;
            a-=f;
            if(a==0) break;
        }
    }
    if(a) d[u]=-1;
    return flow;
}
double dinic(){
    double flow=0;
    while(bfs()){
        for(int i=s;i<=t;i++) cur[i]=h[i];
        flow+=dfs(s,INF);
    }
    //printf("dinic %lf\n",flow);
    return flow;
}

void bfsSol(){
    head=tail=1;
    memset(vis,0,sizeof(vis));
    q[tail++]=s;vis[s]=1;
    while(head!=tail){
        int u=q[head++];
        for(int i=h[u];i;i=e[i].ne){
            int v=e[i].v;
            if(!vis[v]&&e[i].c>e[i].f){
                vis[v]=1;
                q[tail++]=v;
            }
        }
    }
}

bool check(double x){
    cnt=0;
    memset(h,0,sizeof(h));
    for(int i=1;i<=n;i++) ins(i,t,x);
    for(int i=1;i<=m;i++){
        ins(s,n+i,1);
        ins(n+i,u[i],INF);
        ins(n+i,v[i],INF);
    }
    return m-dinic()>eps;//eps
}
void solve(){
    double l=1.0/n,r=m,eps=1.0/(n*n),ans=0;
    while(r-l>eps){
        double mid=(l+r)/2;//printf("erfen %lf %lf %lf\n",l,r,mid);
        if(check(mid)) ans=max(ans,mid),l=mid+eps;
        else r=mid-eps;
    }
    //printf("hi %lf\n",l);
    check(ans);
    bfsSol();
    int num=0;
    for(int i=1;i<=n;i++) if(vis[i]) num++;
    printf("%d\n",num);
    for(int i=1;i<=n;i++) if(vis[i]) printf("%d\n",i);
}
int main(){
    //freopen("in.txt","r",stdin);
    n=read();m=read();s=0;t=n+m+1;
    if(!m){printf("1\n1");return 0;} 
    for(int i=1;i<=m;i++) u[i]=read(),v[i]=read();
    solve();
}