机器学习——利用SVD简化数据
Posted tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习——利用SVD简化数据相关的知识，希望对你有一定的参考价值。
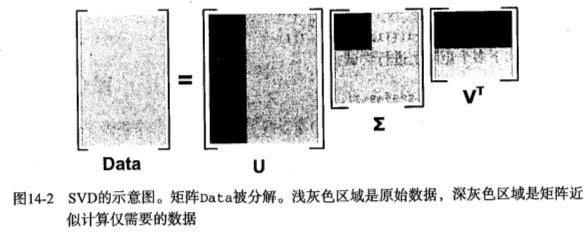
奇异值分解（Singular Value Decompositon,SVD），可以实现用小得多的数据集来表示原始数据集。
优点：简化数据，取出噪声，提高算法的结果
缺点：数据的转换可能难以理解
适用数据类型：数值型数据
SVD最早的应用之一是信息检索，我们称利用SVD的方法为隐形语义索引（LSI）或者隐形语义分析（LSA）。
在LSI中，一个矩阵是有文档和词语组成的。当我们在该矩阵上应用SVD的时候，就会构建出多个奇异值。这些奇异值代表了文档中的概念或者主题，这一特点可以用于更高效的文档检索。
SVD的另一个应用就是推荐系统。简单版本的推荐系统能够计算项或者人之间的相似度。更先进的方法则先利用SVD从数据中构建一个主题空间，然后再在该空间下计算其相似度。
SVD将原始的数据集矩阵Data分解成三个矩阵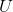 
、
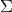和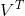 
。
如果数据集矩阵Data是M×N的，那么 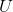是M×M的、 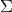是M×N的、 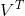是N×N的。
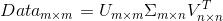
矩阵 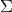中只有从大到小排列的对角元素。在某个奇异值的数目（r个）之后，其他的奇异值都置为0，这就意味这数据集中仅有r个重要特征，而其余特征则都是噪声或者冗余特征。
利用Python实现SVD
>> X=[0.3619 0.2997 0.1331 0.3296;0.1695 0.3628 0.0817 0.2826;0.1159 0.5581 0.0828 0.3718;0.1508 0.1077 0.0539 0.1274] #Matlab
X =
0.3619 0.2997 0.1331 0.3296
0.1695 0.3628 0.0817 0.2826
0.1159 0.5581 0.0828 0.3718
0.1508 0.1077 0.0539 0.1274
>> [U,S,V] = svd (X) #Matlab
U =
-0.5468 0.6999 0.1302 -0.4406
-0.4846 -0.0839 0.5883 0.6420
-0.6496 -0.6312 -0.3105 -0.2883
-0.2102 0.3234 -0.7352 0.5574
S =
1.0245 0 0 0
0 0.2608 0 0
0 0 0.0001 0
0 0 0 0.0000
V =
-0.3778 0.8233 -0.4206 -0.0508
-0.7076 -0.5297 -0.3661 -0.2911
-0.1733 0.1974 0.6302 -0.7307
-0.5715 0.0518 0.5403 0.615
Python
>>> from numpy import *
>>> U,Sigma,VT = linalg.svd([[0.3619,0.2997,0.1331,0.3296],[0.1695,0.3628,0.0817,0.2826],[0.1159,0.5581,0.0828,0.3718],[0.1508,0.1077,0.0539,0.1274]])
>>> U
array([[-0.54683102, 0.69993064, 0.13018303, -0.44059655],
[-0.48455132, -0.08387773, 0.58827674, 0.64195407],
[-0.64962251, -0.63124863, -0.31049494, -0.28828573],
[-0.21018197, 0.32339881, -0.73523857, 0.55736971]])
>>> Sigma
array([ 1.02445357e+00, 2.60778615e-01, 8.12946379e-05,
3.22769863e-05])
>>> VT
array([[-0.37777826, -0.70756881, -0.17325197, -0.57150129],
[ 0.82328242, -0.52968851, 0.19737725, 0.05175294],
[-0.42060604, -0.36612216, 0.63019332, 0.5402791 ],
[-0.05079576, -0.29108595, -0.73067254, 0.61547251]])
可以看到，在Sigma矩阵中8.12946379e-05 和 3.22769863e-05 值的量级太小了，所以可以忽略
所以Data矩阵的值就成了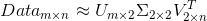 
>>> U,Sigma,VT = linalg.svd([[0.3619,0.2997,0.1331,0.3296],[0.1695,0.3628,0.0817,0.2826],[0.1159,0.5581,0.0828,0.3718],[0.1508,0.1077,0.0539,0.1274]])
>>> U
array([[-0.54683102, 0.69993064, 0.13018303, -0.44059655],
[-0.48455132, -0.08387773, 0.58827674, 0.64195407],
[-0.64962251, -0.63124863, -0.31049494, -0.28828573],
[-0.21018197, 0.32339881, -0.73523857, 0.55736971]])
>>> Sigma
array([ 1.02445357e+00, 2.60778615e-01, 8.12946379e-05,
3.22769863e-05])
>>> VT
array([[-0.37777826, -0.70756881, -0.17325197, -0.57150129],
[ 0.82328242, -0.52968851, 0.19737725, 0.05175294],
[-0.42060604, -0.36612216, 0.63019332, 0.5402791 ],
[-0.05079576, -0.29108595, -0.73067254, 0.61547251]])
>>> Sig3 = mat([[Sigma[0],0,0],[0,Sigma[1],0],[0,0,Sigma[2]]])
>>> U[:,:3]*Sig3*VT[:3,:]
matrix([[ 0.36189928, 0.29969586, 0.13308961, 0.32960875],
[ 0.16950105, 0.36280603, 0.08171514, 0.28258725],
[ 0.11589953, 0.55809729, 0.0827932 , 0.37180573],
[ 0.15080091, 0.10770524, 0.05391314, 0.12738893]])
>>> import numpy as np
>>> U
array([[-0.54683102, 0.69993064],
[-0.48455132, -0.08387773],
[-0.64962251, -0.63124863],
[-0.21018197, 0.32339881]])
>>> Sigma
array([[ 1.02445357, 0. ],
[ 0. , 0.26077861]])
>>> VT
array([[-0.37777826, -0.70756881, -0.17325197, -0.57150129],
[ 0.82328242, -0.52968851, 0.19737725, 0.05175294]])
>>> M = np.dot(U,Sigma)
>>> np.dot(M,VT) #可以使用np.dot进行矩阵乘法
array([[ 0.36190373, 0.29969974, 0.13308294, 0.32960304],
[ 0.16952117, 0.36282354, 0.081685 , 0.28256141],
[ 0.11588891, 0.55808805, 0.08280911, 0.37181937],
[ 0.15077578, 0.10768336, 0.05395081, 0.12742122]])
经过SVD之后生成的三个矩阵相乘，得到的结果和原来的矩阵差不多
基于协同过滤（collaborative filtering）的推荐引擎
协同过滤是通过将用户和其他用户的数据进行对比来实现推荐的。这里的数据是从概念上组织成了类似矩阵的形式。当数据采用这种方式进行组织的时候，我们就可以比较用户或者物品之间的相似度。比如，如果电影和用户看过的电影之间的相似度很高，推荐算法就会认为用户喜欢这部电影。
相似度计算
第一种：使用欧式距离，相似度=1/（1+距离）
当距离为0的时候，相似度为1；当距离很大的时候，相似度趋近于0
第二种：皮尔逊相关系数
皮尔逊相关系数度量的是两个向量之间的相似度，相对于欧式距离的一个优势是，它对用户评级的量级并不敏感。
皮尔逊相关系数的取值范围在-1到+1之间，在NumPy中由函数corrcoef()计算
第三种：余弦相似度
余弦相似度计算的是两个向量夹角的余弦值，如果夹角为90度，则相似度为0；如果两个向量的方向相同，则相似度为1
余弦相似度的取值范围在-1到+1之间，在NumPy中由函数linalg.norm()计算
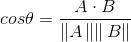
from numpy import *
from numpy import linalg as la
def ecludSim(inA,inB): #欧式距离
return 1.0/(1.0 + la.norm(inA - inB))
def pearsSim(inA,inB): #皮尔逊相关系数
if len(inA) < 3 : return 1.0
return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]
def cosSim(inA,inB): #余弦相似度
num = float(inA.T*inB)
denom = la.norm(inA)*la.norm(inB)
return 0.5+0.5*(num/denom)
# coding:utf-8 # !/usr/bin/env python import svdRec from numpy import * if __name__ == \'__main__\': myMat = mat(svdRec.loadExData()) print svdRec.ecludSim(myMat[:,0],myMat[:,4]) #矩阵第一列和第五列的欧氏距离相似度 print svdRec.pearsSim(myMat[:,0],myMat[:,4]) #矩阵第一列和第五列的皮尔逊相关系数相似度 print svdRec.cosSim(myMat[:,0],myMat[:,4]) #矩阵第一列和第五列的余弦相似度
0.129731907557 0.205965381738 0.5
以上是关于机器学习——利用SVD简化数据的主要内容，如果未能解决你的问题，请参考以下文章