BZOJ 1303 CQOI2009中位数图

Posted 2020-08-27

baidu了一下bzoj水题列表。。。找到这道题。

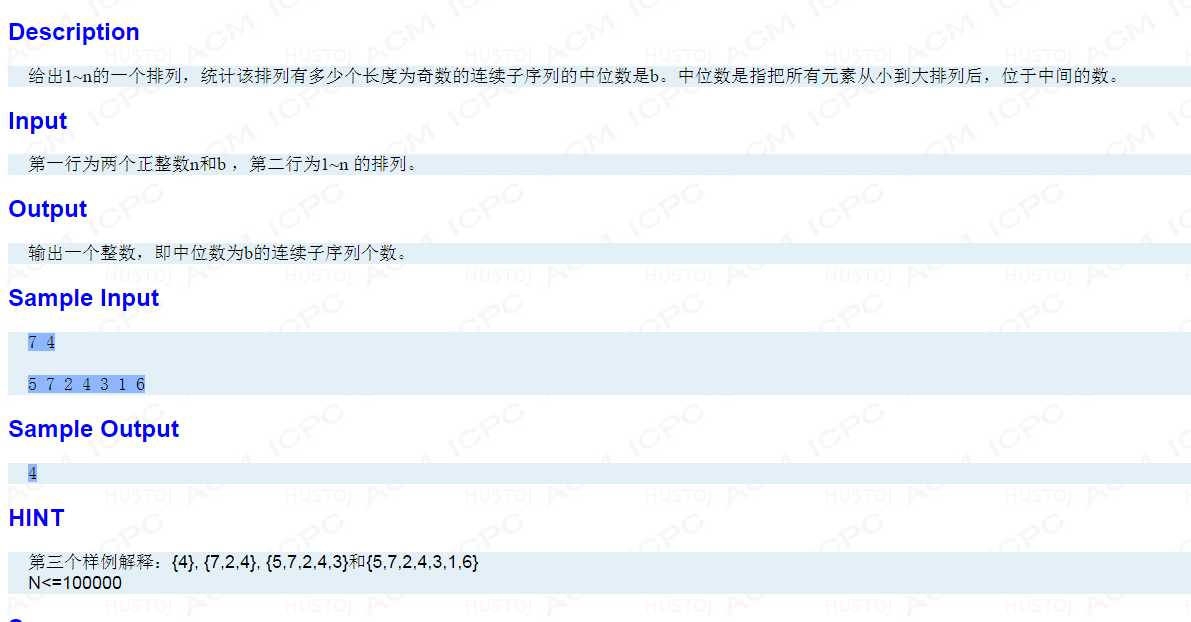
  题目大意：给定一个数t，在给定的一段包含1-n的序列中找出多少个长度为奇数子序列的中位数为t。

  第一眼没看数据范围，于是开心的打了一个O（n^3）的循环，TLE....

  想了想，子序列中必须包含t，所以子序列中其他数的个数必定为偶数，所以子序列中有t以及n个大于t的数和n个小于t的数（n为偶数）；

  因为是1-n的排列，所以也不会出现多个t的情况。。

  于是发现了一个很神奇的思路，对于序列里任何一个数，把小于t的数定义为-1，等于t的数定义为0，大于t的数定义为1，所以只要求出有多少长度为奇数的子序列和为零。。

  于是开心地写了一波前缀和，样例一直没过，后来发现sum【0】没算进去，于是直接在sum【1】塞了一个0，其他往后面一位移。。

  然而枚举的时候脑子有病打了个二重循环，继续TLE....

  后来不知道怎么搞，走了一圈回来突然发现可以用桶排的思想，找出b在序列中的位置k，枚举1-k-1，用一个数组a记录sum数组1-k-1中出现的次数且位置为奇数，数组b记录sum数组1-k-1中出现的次数且位置为偶数，然后再一重循环j枚举k-n，

  看j为偶数和a【sum【j】】是否为大于零，如果是加到ans里面，当j为奇数和b【sum【j】】是否大于零，如果是加到ans里面。。  （tips：奇-偶=奇，偶-奇=奇，所以要分成两个情况处理，使序列长度为奇数）；

  于是又开心的交了一波 。。 Wrong Answer。。。

  于是一直卡Wrong Answer。。。

  第二天才发现数据范围100000然而我看错开的是10000，内心崩溃。。。 改了一下交上去就A了。。。

  下面是代码，其实只有十几行：

 1 var
 2   n,x,t,i,j,k,ans:longint;
 3   sum,a,b:array[-1..1000001]of longint;  //序列中有-1，注意开到-1
 4 begin
 5   readln(n,t);
 6   sum[1]:=0;  //前缀和数组强行塞0；
 7   inc(N); //sum数组有n+1个数据，为了方便循环直接把n+1
 8   for i:=2 to n do begin
 9     read(x);  //读入
10     if x=t then k:=i;  //找出中位数在序列中的位置
11     if x<t then x:=-1
12     else if x=t then x:=0
13     else if x>t then x:=1;
14     sum[i]:=sum[i-1]+x;  //前缀和
15   end;
16   for i:=0 to k-1 do  //从0枚举
17     if i mod 2=1 then inc(a[sum[i]])
18     else inc(b[sum[i]]);  //桶排思想
19     for i:=k to n do
20       if i mod 2=1 then begin
21         inc(ans,b[sum[i]])
22       end
23       else begin
24         inc(ans,a[sum[i]]);
25       end;  //枚举答案
26   write(ans); //输出答案
27 end.

View Code

BZOJ继a+b后ac的第二题，哈哈哈。。。