机器学习笔记模型评估与选择
Posted fjssharpsword
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习笔记模型评估与选择相关的知识,希望对你有一定的参考价值。
2.模型评估与选择
2.1经验误差和过拟合
不同学习算法及其不同参数产生的不同模型,涉及到模型选择的问题,关系到两个指标性,就是经验误差和过拟合。
1)经验误差
错误率(errorrate):分类错误的样本数占样本总数的比例。如果在m个样本中有a个样本分类错误,则错误率E=a/m,相应的,1-a/m称为精度(accuracy),即精度=1-错误率。
误差(error):学习器的实际预测输出和样本的真实输出之间的差异。训练误差或经验误差:学习器在训练集上的误差;泛化误差:学习器在新样本上的误差。
自然,理想情况下,泛化误差越小的学习器越好,但现实中,新样本是怎样的并不知情,能做的就是针对训练集的经验误差最小化。
那么,在训练集上误差最小、甚至精度可到100%的分类器,是否在新样本预测是最优的吗?
我们可以针对已知训练集设计一个完美的分类器,但新样本却是未知,因此同样的学习器(模型)在训练集上表现很好,但却未必在新样本上同样优秀。
2)过拟合
学习器首先是在训练样本中学出适用于所有潜在样本的普遍规律,用于正确预测新样本的类别。这会出现两种情况,导致训练集上表现很好的学习器未必在新样本上表现很好。
过拟合(overfitting):学习器将训练样本的个体特点上升到所有样本的一般特点,导致泛化性能下降。
欠拟合(underfitting):学习器未能从训练样本中学习到所有样本的一般特点。
通俗地说,过拟合就是把训练样本中的个体一般化,而欠拟合则是没学习到一般特点。一个是过犹不及;一个是差之毫厘。过拟合是学习能力太强,欠拟合是学习能力太弱。
欠拟合通过调整模型参数可以克服,但过拟合确实无法彻底避免。机器学习的问题是NP难,有效的学习算法可在多项式时间内完成,如能彻底避免过拟合,则通过经验误差最小化就能获得最优解,这样构造性证明P=NP,但实际P≠NP,过拟合不可避免。
总结,在模型选择中,理想的是对候选模型的泛化误差进行评估,选择泛化误差最小的模型,但实际上无法直接获得泛化误差,需要通过训练误差来评估,但训练误差存在过拟合现象也不适合作为评估标准,如此,如何进行模型评估和选择呢?
2.2评估方法
评估模型既然不能选择泛化误差,也不能选择训练误差,可以选择测试误差。所谓测试误差,就是建立测试样本集,用来测试学习器对新样本的预测能力,作为泛化误差的近似。
测试集,也是从真实样本分布中独立同分布采样而得,和训练集互斥。通过测试集的测试误差来评估模型,作为泛化误差的近似,是一个合理的方法。对数据集D={(x1,y1), (x2,y2),…, (xm,ym)}进行分隔,产生训练集S和测试集T,通过训练集生成模型,并应用测试集评估模型。文中有个很好的例子,就是训练集相当于测试题、而测试集相当于考试题。
现在我们将问题集中在测试集的测试误差上,用以评估模型。那重要的是,对数据集D如何划分成训练集和测试集从而获得测试误差?
1)留出法
留出法(hold-out)将数据集D划分为两个互斥的集合,其中一个集合用作训练集S,另一个作为测试集T,即D=SUT,S∩T=∅。在S上训练出的模型,用T来评估其测试误差,作为对泛化误差的近似估计。
以二分类任务为例。假定D包含1000个样本,将其划分为700个样本的训练集S和300个样本的测试集T。用S训练后,模型在T上有90个样本分类错误,那么测试误差就是90/300=30%,相应地,精度为1-30%=70%。
留出法就是把数据集一分为不同比例的二,这里面就有两个关键点,一个就是如何分?另一个就是分的比例是多少?
如何分呢?训练集和测试集的划分要保持数据分布的一致性。何意?分层采样,保持样本的类别比例相似,就是说样本中的各类别在S和T上的分布要接近,比如A类别的样本的比例是S:T=7:3,那么B类别也应该接近7:3这个分布。
在分层采样之上,也存在不同的划分策略,导致不同的训练集和测试集。显然,单次使用留出法所得到的估计结果不够稳定可靠,一般情况下采用若干次随机划分、重复进行试验评估后取平均值作为评估结果。
S和T各自分多少呢?若训练集S过多而测试集T过小,S越大越接近D,则训练出的模型更接近于D训练出的模型,但T小,评估结果可能不够稳定准确;若训练集S偏小而测试集T偏多,S和D差距过大,S训练的模型将用于评估,该模型和D训练出的模型可能有较大差别,从而降低评估结果的保证性(fidelity)。S和T各自分多少,没有完美解决方法,通常做法是二八开。
2)交叉验证法
交叉验证法(crossvalidation)将数据集D划分为k个大小相似的互斥子集,即D=D1UD2U…UDk,Di∩Dj=∅(i≠j);每个子集Di都尽可能保持数据分布的一致性,即从D中通过分层采样所得。训练时,每次用k-1个子集的并集作为训练集,余下的一个子集作为测试集;如此,可获得k组训练集和测试集,从而进行k次训练和测试,最终返回k次测试结果的均值。k值决定了交叉验证法评估结果的稳定性和保真性,因此也称为k折交叉验证或k倍交叉验证,k常取值10、5、20,10折交叉验证示意图如下:
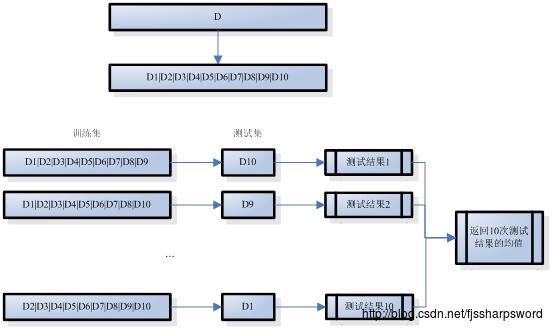
和留出法一样,将数据集D划分为k个子集也是多样划分方式,为减小样本划分不同而发生的差别,k折交叉验证通常随机使用不同的划分重复p次,最后评估结果是这p次k折交叉验证结果的均值,如10次10折交叉验证。
典型的划分特例留一法(Leave-One-Out,LOO),假设数据集D中包含m个样本,令k=m,就是每个子集只包含一个样本。这个特例,不受随机样本划分方式的影响,且训练集S只比数据集D少一个样本,其实际训练出的模型和期望评估的用D训练出的模型相似,其评估结果比较准备。当然,问题就是一个样本一个子集,一旦样本过大,训练的模型所需开销也是极其庞大,且其评估结果也未必比其他方法准确。
实际,所有算法都是如此,有其优点有其缺点,各有适用场合,符合性价比原则。比如留一法,为了提升理论上的准确性,而牺牲相对明确庞大的开销,效益上是否可取,那要看场合了。
3)自助法
在留出法和交叉验证法中,训练集S的样本数是小于数据集D,因样本规模不同会导致所训练的模型及评估结果偏差。留一法虽然S只少一个样本,但计算规模庞大。那么有没办法避免样本规模影响且能高效计算呢?
自助法,基于自助采样获取训练集和测试集。给定包含m个样本的数据集 ,如何通过自助采样(可重复采样或有放回采样)产生数据集D’呢?自助采样基本过程是:每次随机从D中选一个样本,放入D’,然后将该样本放回初始数据集D中,使得该样本在下次采样时仍有可能被采到;这个过程重复执行m次后,就得到了包含m个样本的数据集D’,规模和D一样,不同的是,D’中部分样本可能重复也有部分样本可能不出现。一个样本在m次自助采样中都没有被采到的概率是(1-1/m)m,取极限得到:
即通过自助采样,初始数据集D中约有36.8%的样本未出现在采样数据集D’中。自助采样后 ,将样本规模和数据集D一样的采样数据集D’作为训练集S=D’,将T=D-D’作为测试集(不在D’中的样本作为测试集)。如此,实际评估的模型(训练集S训练出的)与期望评估的模型(数据集 D训练出的)使用了同样的样本规模(m个样本),同时又有大概36.8%的样本(未在采样数据集D’中)作为测试集T用于测试,产生的测试结果,称为包外估计(out-of-bag estimate)。
每个算法都有自己的使用场合,并不是万能性地好用高效。自助法自助采样产生的数据集D’也是改变了初始数据集D的分布,也会引入估计偏差。自助法适用于数据集较小、难以有效划分训练集和测试。在初始数据量足够时,留出法和交叉验证法更常用一些。为更好地对模型(学习器)进行泛化性能评估,提出了近似的测试误差来评估泛化误差,也就衍生出了留出法、交叉验证法、自助法的数据集划分方法。实际上,算法还需要调参,不同的参数配置,模型的性能会有一定差别。在进行模型评估和选择时,除了选择算法还有数据集划分方法外,还需要对算法参数进行设定或说是调节。每一个算法都有参数设定空间,假定算法有3个参数,每个参数有5个可选值,对每一组训练集/测试集来说就有53=125个模型需要考察。
实际的学习过程中,对给定包含m个样本的数据集D,先选定学习算法及其参数,然后划分数据集训练和测试,直至选定算法和参数,再应用数据集D来重新训练模型。在研究对比不同算法的泛化性能时,用测试集上的判别效果来评估模型在实际使用中的泛化能力,而把训练数据另外划分为训练集和验证集,基于验证集上的性能进行模型选择和调参。
梳理下几个要点:1)将数据集划分为:训练集、验证集、测试集;2)训练集用于训练出模型,验证集用于模型选择和调参,测试集用于近似评估泛化误差;3)模型评估方法有留出法、交叉验证法、自助法,用于算法选择及参数设定。2.3性能度量
通过在训练过程中的评估方法来判定学习器的泛化性能,还需要通过性能度量来考察。换句话来说,选什么模型,通过训练集、验证集、测试集来实验评估选定并输出;而所输出的模型,在测试集中实的泛化能力,需要通过性能度量工具来度量。这样理解,基于测试误差近似泛化误差的认定,通过划分数据集为训练集、验证集、测试集,并选择不同的评估方法和调整算法参数来输出的模型,需要通过性能度量的工具来量化评估。
不同的性能度量,在对比不同模型能力时,会导致不同评判结果,因为模型的好坏是相对的。实际模型的好坏,取决于算法和数据,取决于训练中调参和实验评估方法,也取决于当前任务的实际数据。
模型训练出来后,进行预测时,给定样例集D={(x1,y1), (x2,y2),…, (xm,ym)},其中yi是示例xi的真实标记,要评估学习器f的性能,把学习器预测结果f(x)与真实标记y进行比较。
预测回归任务最常用的性能度量是均方误差(mean squared error):

| 真实情况 | 预测结果 | |
| 正例 | 反例 | |
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假正例) | TN(真反例) |
以上是关于机器学习笔记模型评估与选择的主要内容,如果未能解决你的问题,请参考以下文章