二叉树的外路径长、内路径长及相互关系公式证明

Posted 2023-03-30

二叉树的外路径长、内路径长及相互关系公式证明
外路径长E：从根结点到每个外结点的路径长之和
内路径长I：从根结点到每个内结点的路径长之和
求证：关系： E = I＋2×n (n为内结点的个数）
要求，不得用数学归纳法证明
该题属数据结构题
急。解决该问题可另加分
谢谢你的回答，不过数学上具体如何证明呢？

在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2^i-1个结点；深度为k的二叉树至多有2^k-1个结点；对任何一棵二叉树T，如果其终端结点数为n_0，度为2的结点数为n_2，则n_0=n_2+1。

一棵深度为k，且有2^k-1个节点称之为满二叉树；深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时，称之为完全二叉树。

二叉树性质

(1) 在非空二叉树中，第i层的结点总数不超过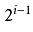, i>=1；

(2) 深度为h的二叉树最多有个结点(h>=1)，最少有h个结点；

(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

(4) 具有n个结点的完全二叉树的深度为

(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

若I为结点编号则 如果I>1，则其父结点的编号为I/2；

如果2*I<=N，则其左儿子（即左子树的根结点）的编号为2*I；若2*I>N，则无左儿子；

如果2*I+1<=N，则其右儿子的结点编号为2*I+1；若2*I+1>N，则无右儿子。

(6)给定N个节点，能构成h(N)种不同的二叉树。

h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。

(7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i

参考技术A 请看LL分析：

首先你说的二叉树是只有一个根节点，每个节点两个分叉的二叉树是吧
其实很简单了
每个内节点是有2个 向下的分支
比如我们取从上到下的顺序看这个2叉树
重点注意倒数第二层的节点

其实E和I 相差的就是 2n
2n是什么，就是每个内节点申出来的2个径了
我不知道你们老师怎么讲的，数据结构是要讲二叉树的，
我给学生讲的时候就是这么说的，
其实很直观的！ 参考技术B 首先你说的二叉树是只有一个根节点，每个节点两个分叉的二叉树是吧
其实很简单了
每个内节点是有2个 向下的分支
比如我们取从上到下的顺序看这个2叉树
重点注意倒数第二层的节点

其实E和I 相差的就是 2n
2n是什么，就是每个内节点申出来的2个径了
我不知道你们老师怎么讲的，数据结构是要讲二叉树的，
我给学生讲的时候就是这么说的，
其实很直观的！本回答被提问者采纳 参考技术C 不对吧，这是应该对完全二叉树适用的吧！
对于完全二叉树来讲，这个定理入楼上所说的那样！但是普通二叉树就不一定了啊！

lintcode:二叉树的所有路径

二叉树的所有路径

给一棵二叉树，找出从根节点到叶子节点的所有路径。

样例

给出下面这棵二叉树：

   1
 /   2     3
   5

所有根到叶子的路径为：

[
  "1->2->5",
  "1->3"
]

解题
深度优先 可以转换成先序遍历：根左右，根结点遍历以后，遍历两个子树，是叶子结点的时候保存路径

/**
 * Definition of TreeNode:
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left, right;
 *     public TreeNode(int val) {
 *         this.val = val;
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    /**
     * @param root the root of the binary tree
     * @return all root-to-leaf paths
     */
    public ArrayList<String> binaryTreePaths(TreeNode root) {
        // Write your code here
        ArrayList<String> result = new ArrayList<String>();
        if(root == null)
            return result;
        String path="";
        Paths(root,result,path);
        return result;
    }
    public void Paths(TreeNode root,ArrayList<String> result,String path){
        if(root == null)
            return;
        if(root.left==null && root.right == null){
            if( path.equals(""))
                path += root.val;
            else 
                path +="->"+root.val;
            result.add(path);
            return;
        }
        if( path.equals(""))
            path += root.val;
        else 
            path +="->"+root.val;
        Paths(root.left,result,path);
        Paths(root.right,result,path);
        
    }
}

 

后面两行代码互换对结果没有影响，只是所有路径的先后次序发生了变化

Paths(root.right,result,path);
Paths(root.left,result,path);