如何实现地理位置与经纬度坐标的批量转换
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何实现地理位置与经纬度坐标的批量转换相关的知识,希望对你有一定的参考价值。
现在有软件能实现批量转换了,就算没有编程经验也可以。下面以LSV为例,介绍如何实现地理位置与经纬度坐标的批量转换,还是双向的噢,就是地理编码与逆地理编码都可以操作。
批量地址查询(地理编码)教程如下
步骤1:点击批量地址查询:
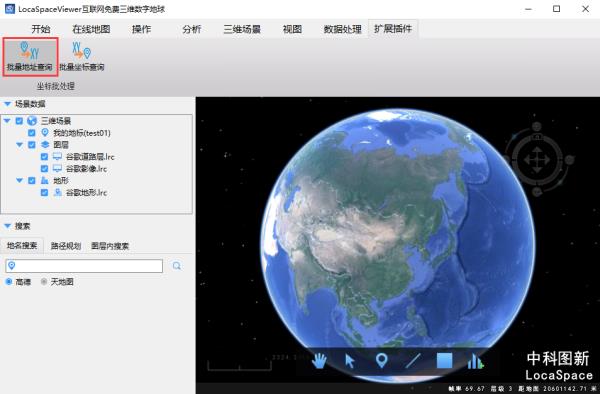
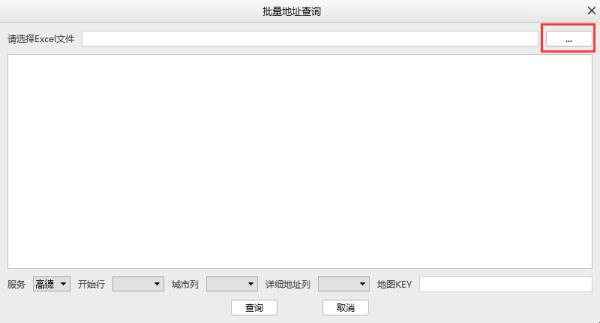
步骤2:选择要进行处理的Excel文件:
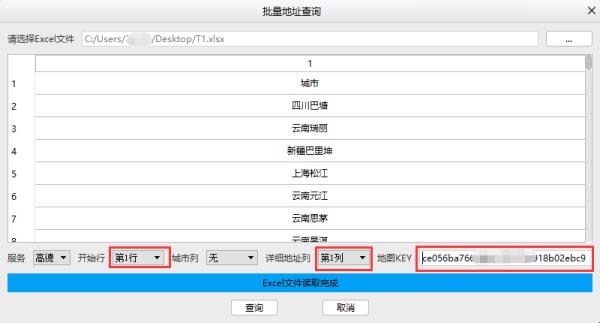
步骤3:Excel加载完成后,配置对应的数据开始行、详细地址列、地图KEY:
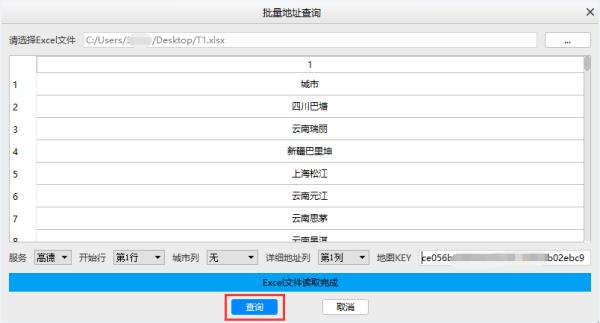
步骤4:点击查询,设置输出文件地址:
步骤5:即可快速进行批量查询:
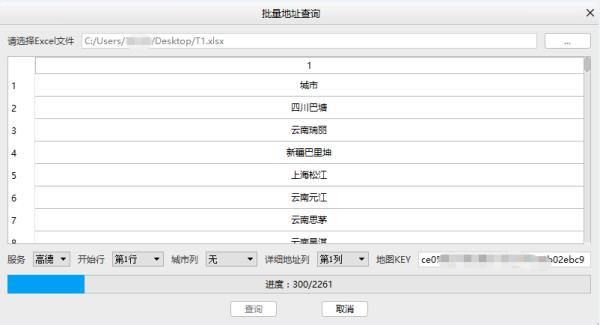
步骤6:查询完成后,会看到结果提示:
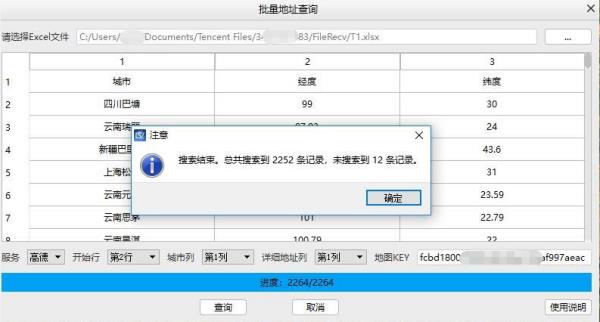
步骤7:打开输出文件可以查看查询结果:
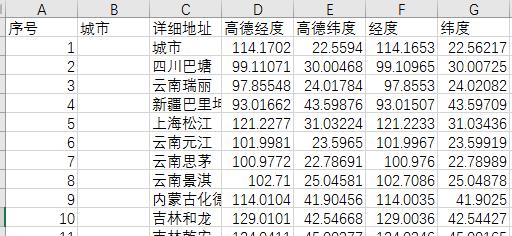
其实高德经度、高德纬度为高德坐标(GJC02),经度、纬度为WGS84坐标。
如果要把查询结果转换为KML,可继续使用这个软件把Excel转KML功能。
这里面用的是高德的API,需要去高德申请,也不麻烦。这里就不赘述了。
批量坐标查询操作(逆地理编码)教程如下
批量坐标查询(逆地理编码),指现有大量坐标(WGS84)信息存储于Excel内,需要获取地址对应的坐标。
步骤1:点击批量坐标查询,选择Excel文件:
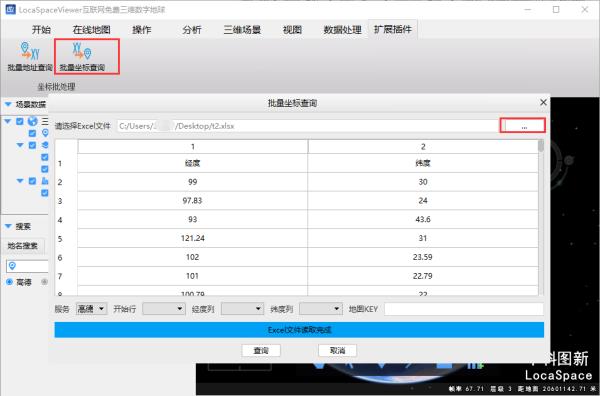
步骤2:设置查询开始行、经度所在列、纬度所在列、地图KEY:
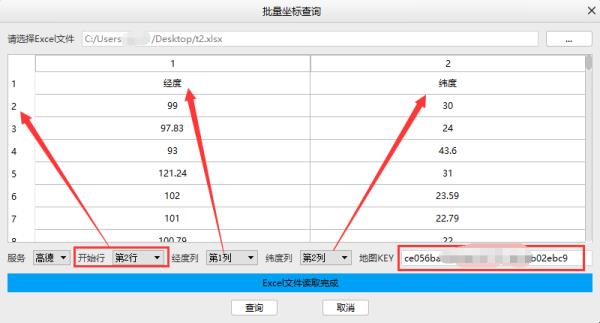
步骤3:点击查询按钮,设置输出路径和文件名,开始批量查询:
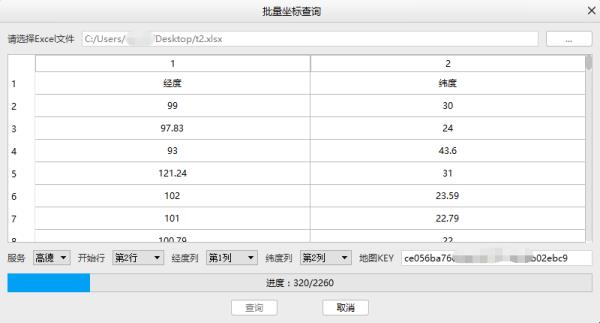
完成后,会看到错误提示。
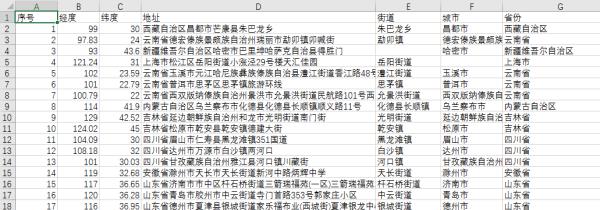
步骤4:打开输出文件可以看到坐标查询结果:
大地经纬度坐标与地心地固坐标的的转换
1. 概述
要解决这个问题首先得理解地球椭球这个概念,这里直接用武汉大学《大地测量学基础》(孔详元、郭际明、刘宗全)的解释吧:

大地经纬度坐标系是地理坐标系的一种,也就是我们常说的经纬度坐标+高度。经纬度坐标用的虽然多,但是很多人并没有理解经纬度的几何意义:纬度是一种线面角度,是坐标点P的法线与赤道面的夹角(注意这个法线不一定经过球心);经度是面面角,是坐标点P所在的的子午面与本初子午面的夹角。这也是为什么经度范围是-180 ~ +180,纬度范围却是-90 ~ +90:

地心地固坐标系就是我们常用的笛卡尔空间直角坐标系了。这个坐标系以椭球球心为原点,本初子午面与赤道交线为X轴,赤道面上与X轴正交方向为Y轴,椭球的旋转轴(南北极直线)为Z轴。显然,这是个右手坐标系:
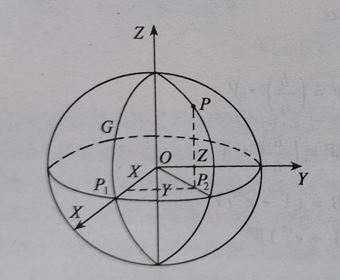
显然,两者都是表达的都是空间中某点P,只不过一个是经纬度坐标(BLH),一个是笛卡尔坐标(XYZ);两者是可以相互转换的。
2. 推导
2.1. BLH->XYZ
将P点所在的子午椭圆放在平面上,以圆心为坐标原点,建立平面直接坐标系:
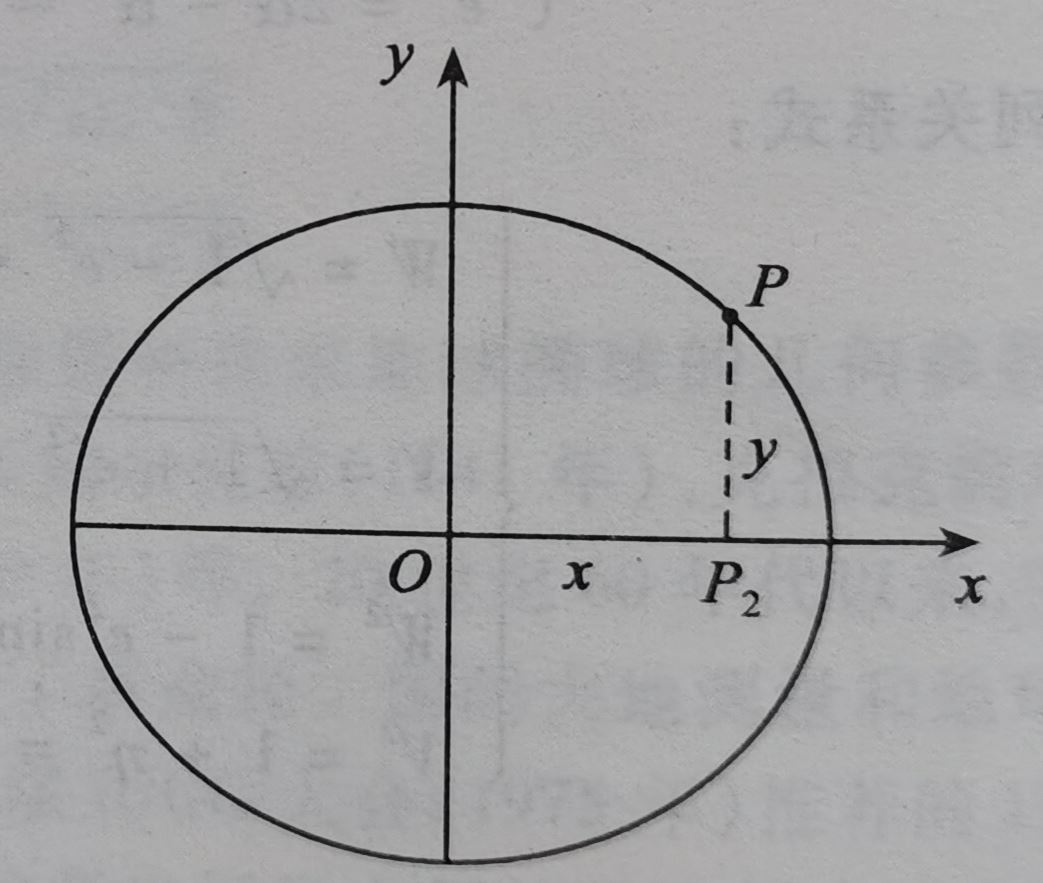
对照地心地固坐标系,很容易得出:
那么,关键问题在于求子午面直角坐标系的x,y。过P点作原椭球的法线Pn,他与子午面直角坐标系X轴的夹角为B;过P点作子午椭圆的切线,它与X轴的夹角为(90°+B):
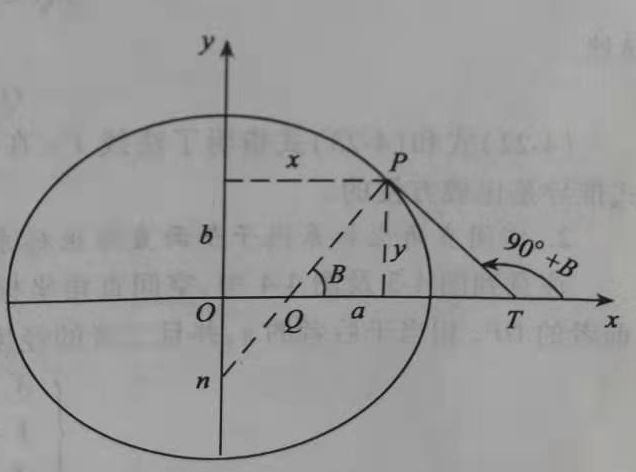
根据椭圆的方程,位于椭圆的P点满足:
对x求导,有:
又根据解析几何可知,函数曲线(椭圆)某一点(就是P点)的倒数为该点切线的斜率,也就是正切值:
联立公式(2)(3),可得:
其中,e为椭圆第一偏心率:
令Pn的距离为N,那么显然有:
根据(4)式可得:
将其带入(1)式,可得到椭球上P点的坐标为:
那么唯一的未知量就是Pn的长度N了,将(4)式带入到椭圆方程式(1.2):
化简,得:
联立式(5)式(6),得:
通过式(5)式(6),可以计算椭球上某一点的坐标。但这个点并不是我们真正要求的点,我们要求的点P(B,L,H)是椭球面沿法向量向上H高度的点:
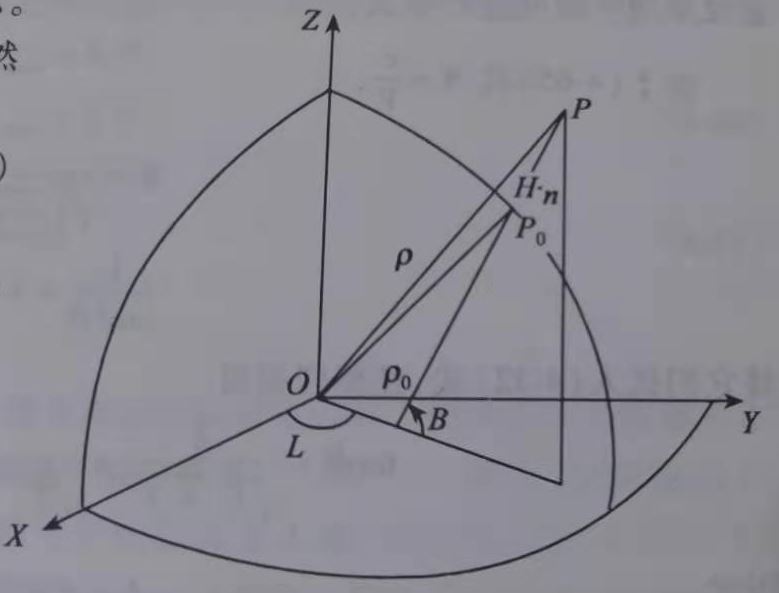
P点在椭球面上的点为\\(P_0\\),那么根据矢量相加的性质,有:
其中,\\(P_0\\)也就是式(5),而n是\\(P_0\\)在椭球面的法线单位矢量。
矢量在任意位置的方向都是一样的,那么我们可以假设存在一个单位球(球的半径为单位1),将法线单位矢量移动到球心位置,可得法线单位矢量为:
因此有:
其中:
2.2. XYZ->BLH
根据式(8),可知:
因此有:
不过纬度B就不是那么好算了,首先需要计算法线Pn在赤道两侧的长度。根据图1,有:
与式(4-3)比较可得:
显然,由于:
有:
接下来如下图所示,对图1做辅助线:
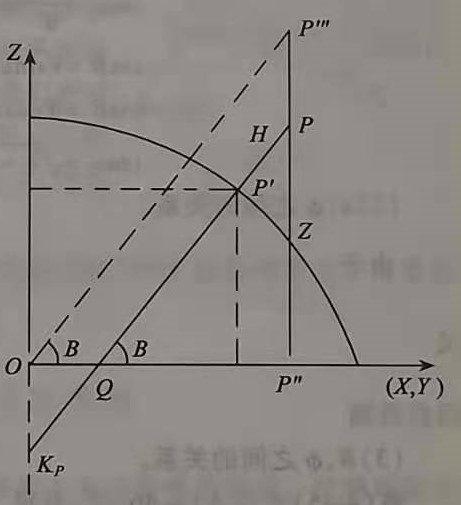
有:
因而可得:
这个式子两边都有待定量B,需要用迭代法进行求值。具体可参看代码实现,初始的待定值可取\\(tanB = \\frac{z}{\\sqrt{x^2+y^2}}\\)。
大地纬度B已知,那么求高度H就非常简单了,直接根据式(8)中的第三式逆推可得:
汇总三式,可得:
3. 实现
根据前面的推导过程,具体的C/C++代码实现如下:
#include <iostream>
using namespace std;
const double epsilon = 0.000000000000001;
const double pi = 3.14159265358979323846;
const double d2r = pi / 180;
const double r2d = 180 / pi;
const double a = 6378137.0; //椭球长半轴
const double f_inverse = 298.257223563; //扁率倒数
const double b = a - a / f_inverse;
//const double b = 6356752.314245; //椭球短半轴
const double e = sqrt(a * a - b * b) / a;
void Blh2Xyz(double &x, double &y, double &z)
{
double L = x * d2r;
double B = y * d2r;
double H = z;
double N = a / sqrt(1 - e * e * sin(B) * sin(B));
x = (N + H) * cos(B) * cos(L);
y = (N + H) * cos(B) * sin(L);
z = (N * (1 - e * e) + H) * sin(B);
}
void Xyz2Blh(double &x, double &y, double &z)
{
double tmpX = x;
double temY = y ;
double temZ = z;
double curB = 0;
double N = 0;
double calB = atan2(temZ, sqrt(tmpX * tmpX + temY * temY));
int counter = 0;
while (abs(curB - calB) * r2d > epsilon && counter < 25)
{
curB = calB;
N = a / sqrt(1 - e * e * sin(curB) * sin(curB));
calB = atan2(temZ + N * e * e * sin(curB), sqrt(tmpX * tmpX + temY * temY));
counter++;
}
x = atan2(temY, tmpX) * r2d;
y = curB * r2d;
z = temZ / sin(curB) - N * (1 - e * e);
}
int main()
{
double x = 113.6;
double y = 38.8;
double z = 100;
printf("原大地经纬度坐标:%.10lf\\t%.10lf\\t%.10lf\\n", x, y, z);
Blh2Xyz(x, y, z);
printf("地心地固直角坐标:%.10lf\\t%.10lf\\t%.10lf\\n", x, y, z);
Xyz2Blh(x, y, z);
printf("转回大地经纬度坐标:%.10lf\\t%.10lf\\t%.10lf\\n", x, y, z);
}
其最关键的还是计算大地纬度B时的迭代过程,其余的计算都只是套公式。数值计算中的很多算法都是采用迭代趋近的方法来趋近一个最佳解。最后的运行结果如下:
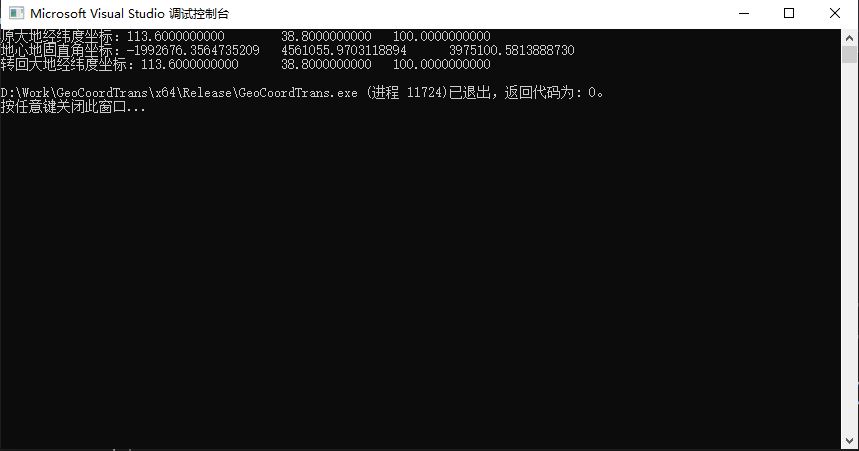
4. 参考
以上是关于如何实现地理位置与经纬度坐标的批量转换的主要内容,如果未能解决你的问题,请参考以下文章