梯度下降法VS随机梯度下降法 (Python的实现)

Posted 2020-06-17

 

 1 # -*- coding: cp936 -*-
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 
 5 
 6 # 构造训练数据
 7 x = np.arange(0., 10., 0.2)
 8 m = len(x)                                      # 训练数据点数目
 9 x0 = np.full(m, 1.0)                 
10 input_data = np.vstack([x0, x]).T               # 将偏置b作为权向量的第一个分量
11 target_data = 2 * x + 5 + np.random.randn(m)
12 
13 
14 # 两种终止条件
15 loop_max = 10000   # 最大迭代次数(防止死循环)
16 epsilon = 1e-3     
17 
18 # 初始化权值
19 np.random.seed(0)
20 w = np.random.randn(2)
21 #w = np.zeros(2)
22 
23 alpha = 0.001      # 步长(注意取值过大会导致振荡,过小收敛速度变慢)
24 diff = 0.           
25 error = np.zeros(2) 
26 count = 0          # 循环次数
27 finish = 0         # 终止标志
28 # -------------------------------------------随机梯度下降算法----------------------------------------------------------
29 ‘‘‘
30 while count < loop_max:
31     count += 1
32 
33     # 遍历训练数据集，不断更新权值
34     for i in range(m):  
35         diff = np.dot(w, input_data[i]) - target_data[i]  # 训练集代入,计算误差值
36 
37         # 采用随机梯度下降算法,更新一次权值只使用一组训练数据
38         w = w - alpha * diff * input_data[i]
39 
40         # ------------------------------终止条件判断-----------------------------------------
41         # 若没终止，则继续读取样本进行处理，如果所有样本都读取完毕了,则循环重新从头开始读取样本进行处理。
42 
43     # ----------------------------------终止条件判断-----------------------------------------
44     # 注意：有多种迭代终止条件，和判断语句的位置。终止判断可以放在权值向量更新一次后,也可以放在更新m次后。
45     if np.linalg.norm(w - error) < epsilon:     # 终止条件：前后两次计算出的权向量的绝对误差充分小  
46         finish = 1
47         break
48     else:
49         error = w
50 print ‘loop count = %d‘ % count,  ‘\tw:[%f, %f]‘ % (w[0], w[1])
51 ‘‘‘
52 
53 
54 # -----------------------------------------------梯度下降法-----------------------------------------------------------
55 while count < loop_max:
56     count += 1
57 
58     # 标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的
59     # 在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算
60     sum_m = np.zeros(2)
61     for i in range(m):
62         dif = (np.dot(w, input_data[i]) - target_data[i]) * input_data[i]
63         sum_m = sum_m + dif
64 
65     w = w - alpha * sum_m  # 注意步长alpha的取值,过大会导致振荡
66     #w = w - 0.005 * sum_m # alpha取0.005时产生振荡,需要将alpha调小
67     
68     # 判断是否已收敛
69     if np.linalg.norm(w - error) < epsilon:
70         finish = 1
71         break
72     else:
73         error = w
74 print ‘loop count = %d‘ % count,  ‘\tw:[%f, %f]‘ % (w[0], w[1])
75 
76 
77 plt.plot(x, target_data, ‘k+‘)
78 plt.plot(x, w[1] * x + w[0], ‘r‘)
79 plt.show()

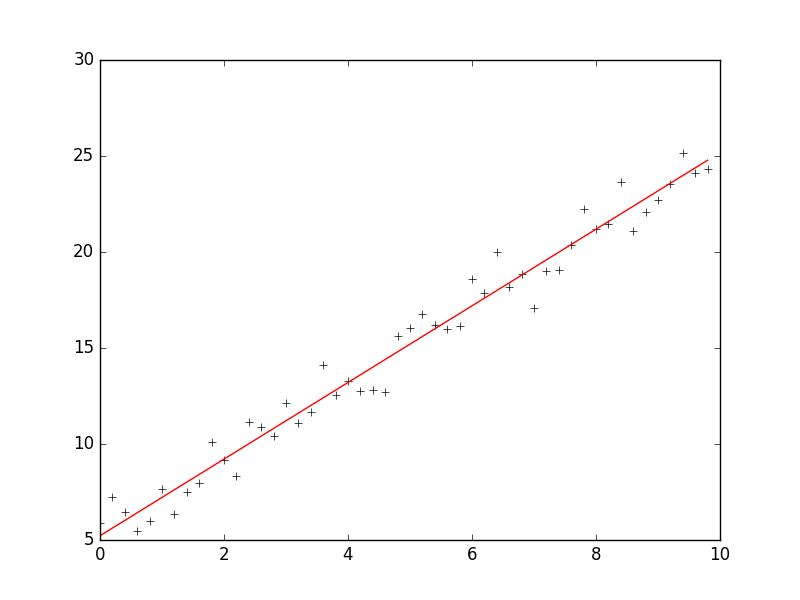
参考：http://www.tuicool.com/articles/MRbee2i