基本数据结构学习笔记——树与二叉树

Posted 2020-06-17

1、树的形式化定义：

     树(Tree)是由一个或多个结点组成的有限集合T，其中有一个特定的称为根的结点；其余结点可分为m(m≥0)个互不相交的有限集T1,T2,T3 ,…,Tm，每一个集合本身又是一棵树，且称为根的子树。

2、有关树的基本术语:

1.结点（Node）：树中的元素，包含数据项及若干指向其子树的分支。

2.结点的度（Degree）：结点拥有的子树数。

3.结点的层次：从根结点开始算起，根为第一层.

4.叶子（Leaf）：度为零的结点，也称端结点。

5.孩子（Child）：结点子树的根称为该结点的孩子结点。

6.双亲（Parent）：孩子结点的上层结点，称为这些结点的双亲。

7.兄弟（Sibling）：同一双亲的孩子。

8.深度（Depth)：  树中结点的最大层次数。

9.森林（Forest）：M棵互不相交的树的集合。

 

3、树的存储结构

1.树的存储结构可以采用具有多个指针域的多重链表，结点中指针域的个数应由树的度来决定

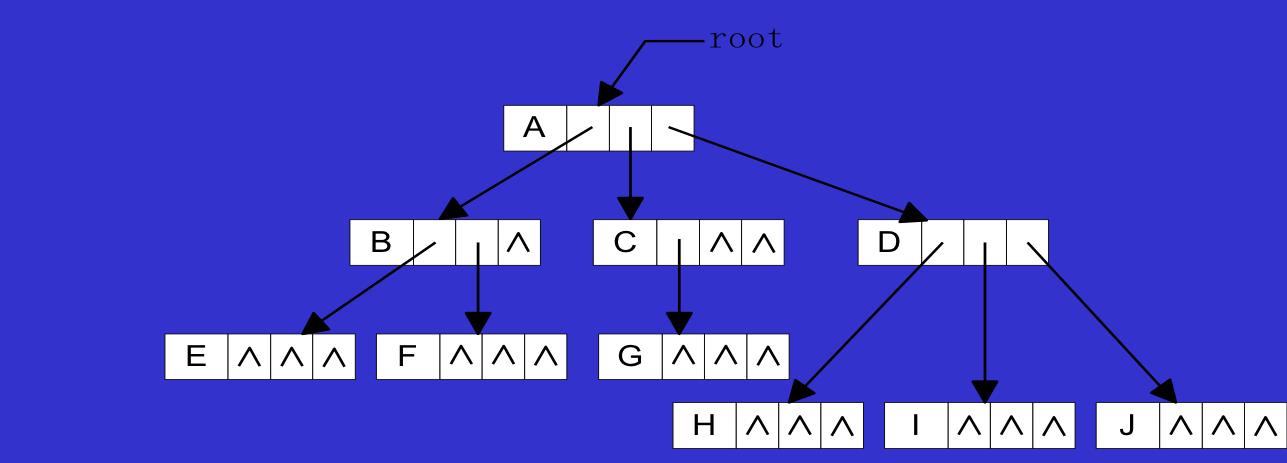
2.但在实际应用中，这种存储结构并不方便，一般将树转化为二叉树表示，进行处理

3.可以用树来表示算术表达式

 

4、二叉树(Binary Tree)的定义

　　二叉树是一种重要的树形结构，其结构定义为：二叉树是n(n≥0)个结点的有限集，它或为空树(n=0)，或由一个根结点和两棵分别称为根的左子树和右子树的、互不相交的二叉树组成。

5、二叉树的性质

 

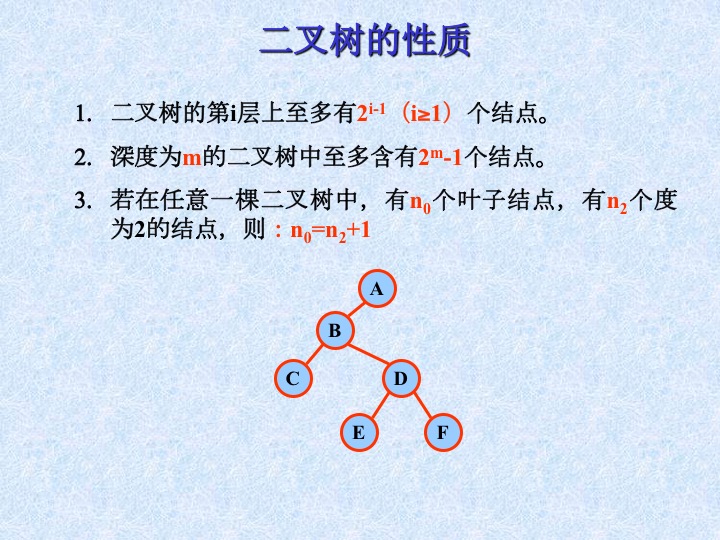
6、满二叉树和完全二叉树

 

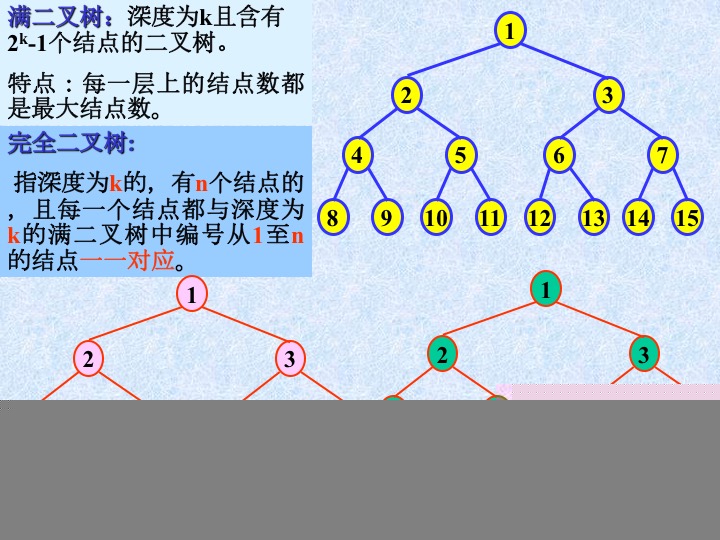
7、二叉树的存储结构

 

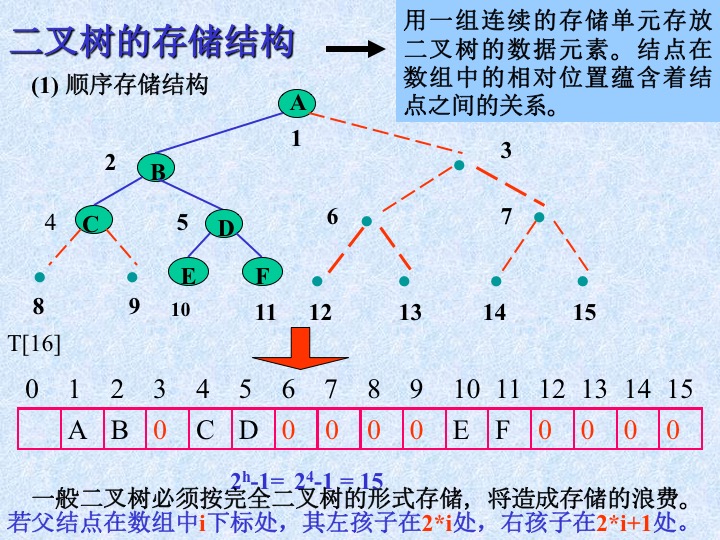
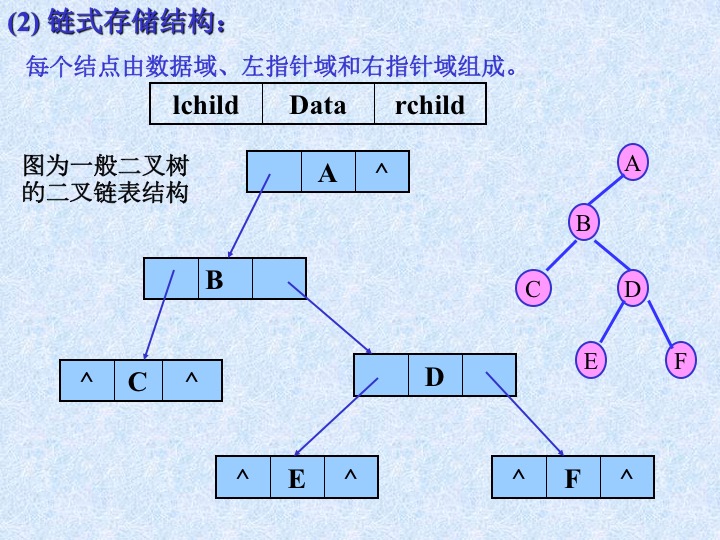
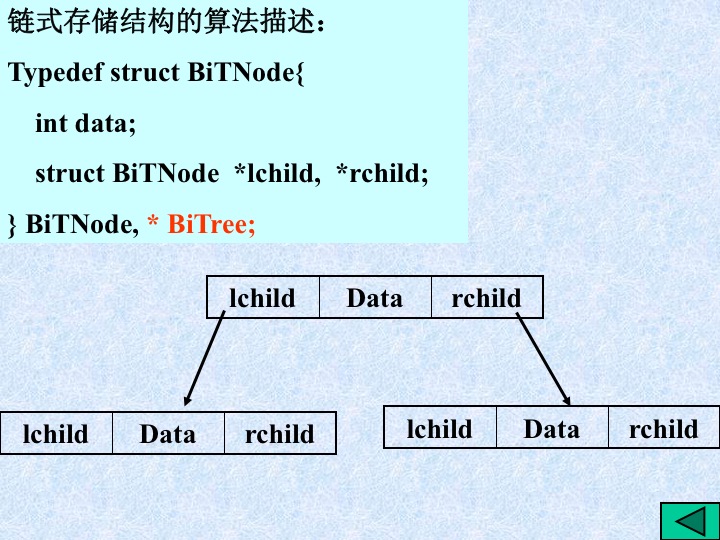
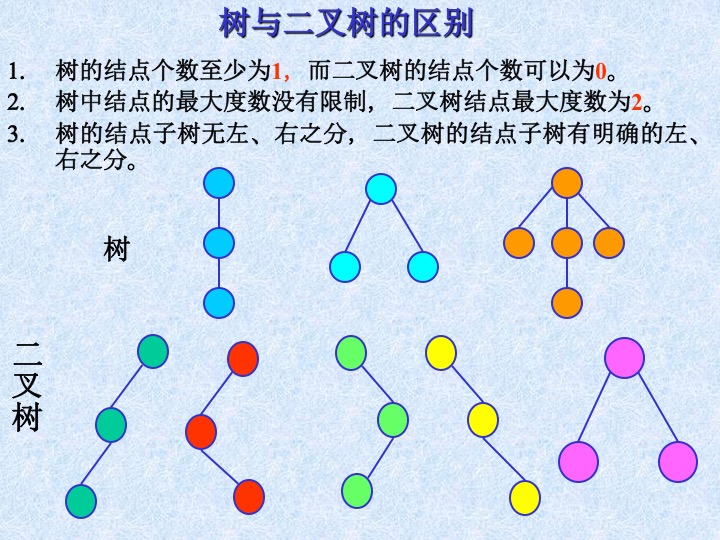
8、树与二叉树的区别

 

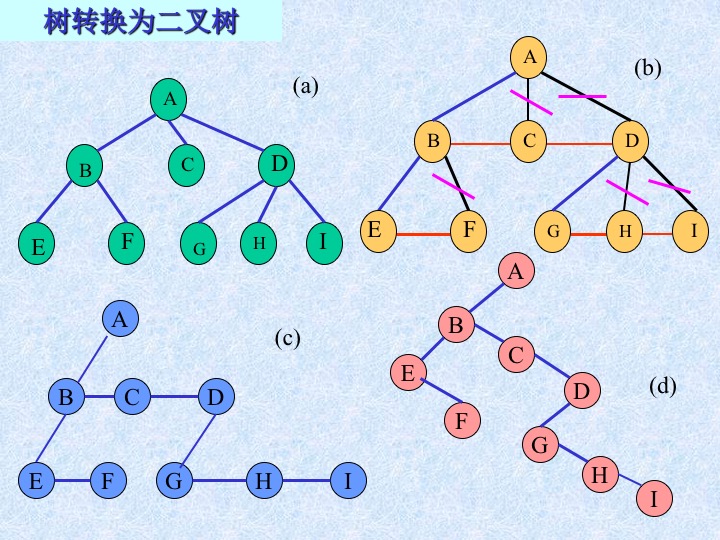
9、树和森林转化为二叉树

 

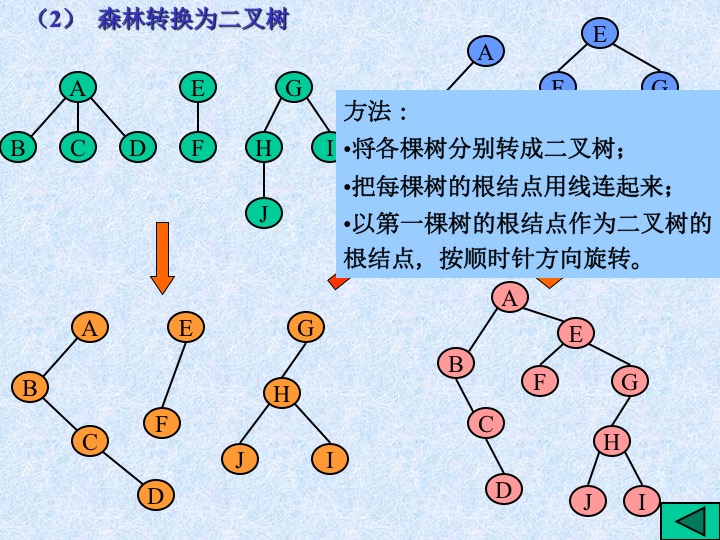
10、二叉树的遍历

 

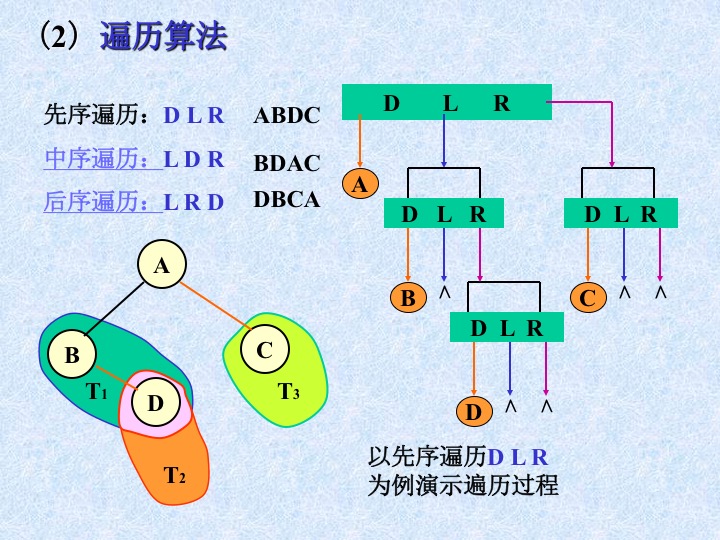
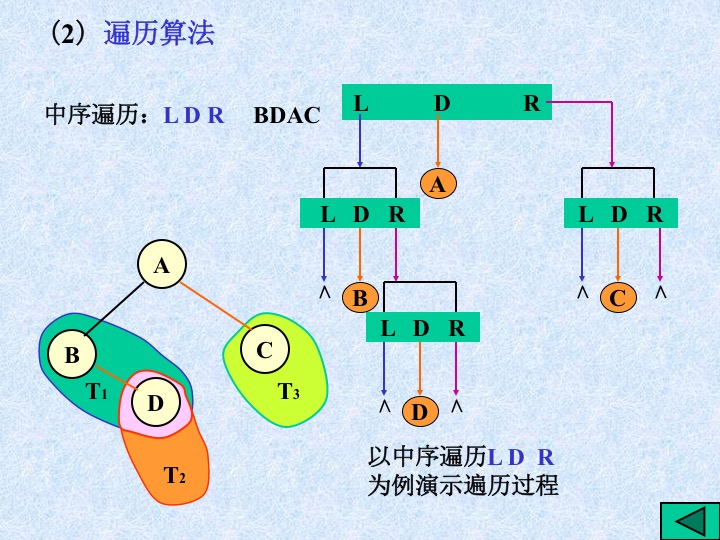
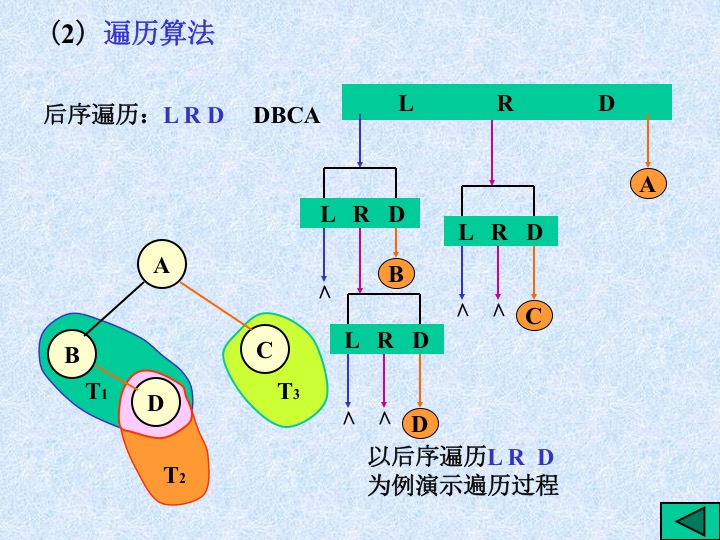
11、建立二叉链表，并进行二叉树的遍历