圆的面积凭什么是 πr²

Posted 2020-08-25 假如你是李华

为什么圆的面积 \\( S = \\pi r^2 \\)? 怎么证？

证法可以有很多，但是那些广为人知的「证法」多多少少都有问题。

小学的证法

切西瓜片？太不严密，不能令人信服：

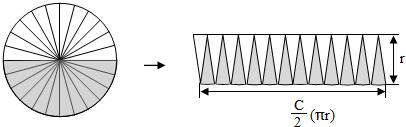
人家圆弧明明是弯的，你凭什么说人家是直的？无论你分成多少份，那圆弧始终都是弯的，拼起来永远都不可能成为平行四边形。逼近也得讲道理，不然对了也是碰巧对了。

要说逼近都是对的的话，用类似的逻辑，也可以证明 \\(\\pi=4\\):

难道这也是对的？

大学的证法

积分？这就陷入了循环论证：

（上图中有点小错误，懒得改了，反正意思大家都明白）

积分就要换元，换元就要回到导数，导数又要回到极限。要证极限 \\(\\lim_\\limits{x \\to 0}\\frac{\\　　sin{x}}{x}=1\\) 的值为 1, 就要利用不等式 \\(\\sin{x}<x<\\tan{x}\\) (\\(x\\) 是锐角) 导出不等式 \\( \\cos{x}<\\frac{\\sin{x}}{x}<1 \\). 那么问题来了：为什么不等式 \\(\\sin{x}<x<\\tan{x}\\) 在锐角范围内成立？教材说，你画个圆，再画个角，由面积关系可知，该不等式 显~然~ 成立。

　　

问题是，扇形 \\(OPA\\) 的面积为什么是 \\(\\frac{1}{2}x\\)? 根据圆完美的对称性可知，圆心角为 x 的扇形，其面积为整个圆的面积的 \\(\\frac{x}{2\\pi}\\) 倍，……

等等，整个圆的面积是多少来着？我现在在求的不就是这个吗？这不又绕回来了？

避免循环论证

那么现在问题来了：循环论证？为什么会这样？到底怎样才能令人信服地推导出圆的面积公式？

要解决这个问题，先想一想，圆的面积公式到底反映了什么。从表面上看其实无非就两点：

一、圆的面积和半径的平方成正比

二、比例系数是圆周率 \\(\\pi\\)

那么圆周率又是什么？圆周率就是直径为单位长度的圆的周长。注意并不是我们算出了这个长度等于圆周率，而是定义了这个长度等于圆周率。所以说，圆的面积公式换个角度可以说反映的是圆的面积和周长（弧长）与半径的关系，即：

\\(S=\\frac{1}{2}CR\\)

知道了这一点，再来想一想极限 \\(\\lim_\\limits{x \\to 0}\\frac{\\sin{x}}{x}=1\\) 的几何意义是什么。这可以有两种理解：

一、当角足够小时，三角形的面积趋近于扇形的面积

二、当角足够小时，弦长趋近于弧长

（那个不等式同理，也可以有面积和弧长两种解释）

之所以上面的方法出现了循环论证，就是因为使用了第一种和面积有关的解释，而此时圆的面积是多少还不知道呢。由此看来，使用第二种解释比较合适。

上面两点都说明了弧长的地位（它是最基本的，因为 \\(\\pi\\) 是用弧长直接定义的）。所以不妨从弧长的角度出发重新考虑一下怎么推出极限 \\(\\lim_\\limits{x \\to 0}\\frac{sin{x}}{x}=1\\).

 

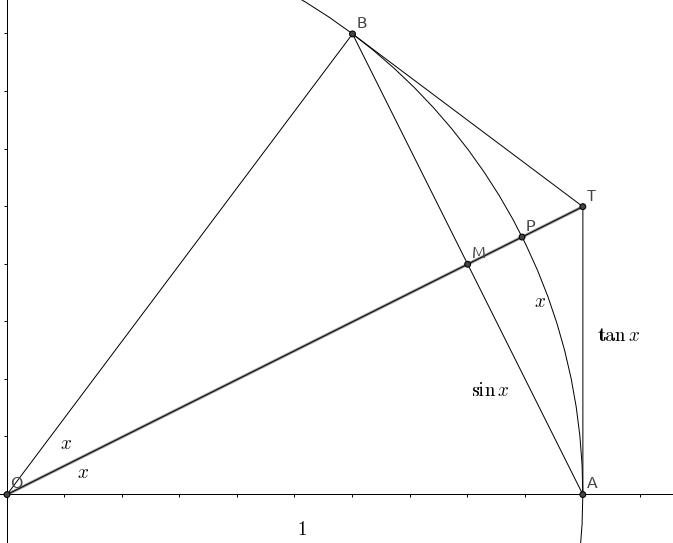
如图，作 \\(\\angle POA=x \\in (0, \\frac{\\pi}{2})\\), 则有 \\(MA=\\sin{x}\\), \\(\\overset{\\frown}{PA}=x\\), \\(TA=\\tan{x}\\). 延长 \\(AM\\) 交圆于 \\(B\\), 连接 \\(OB\\), \\(BT\\) 得到一个对称的风筝形。

如果能证明原来那个不等式 \\(\\sin{x}<x<\\tan{x}\\), 即 \\(MA<\\overset{\\frown}{PA}<TA\\), 就可以推出所求极限。

又因为 \\(MA<\\overset{\\frown}{PA}<TA \\Leftrightarrow 2MA<2\\overset{\\frown}{PA}<2TA \\),

所以只需证 \\(AB<\\overset{\\frown}{AB}<TA+TB\\).

\\( AB<\\overset{\\frown}{AB} \\) 这一点非常直观，两点之间线段最短；\\( \\overset{\\frown}{AB}<TA+TB \\) 这一点也不难看出，毕竟相对于弦 \\(AB\\), 弧 \\(AB\\) 和折线 \\(A-T-B\\) 都是凸的，而折线又在弧的外面，所以折线比弧要长。如果承认这两点，极限就得证了。极限得证了，算出面积就不是问题了。

可能第二点（折线比弧长）有点牵强，但是承认这一点总比陷入循环论证要好得多。事实上古希腊的阿基米德就是靠这两点严格证出的圆的面积公式：

（引自欧阳顺湘翻译的 Bill Casselman 的论文《阿基米德论圆的周长与面积》，以下贴上该文中对这两个引理的说明）

---

 

---

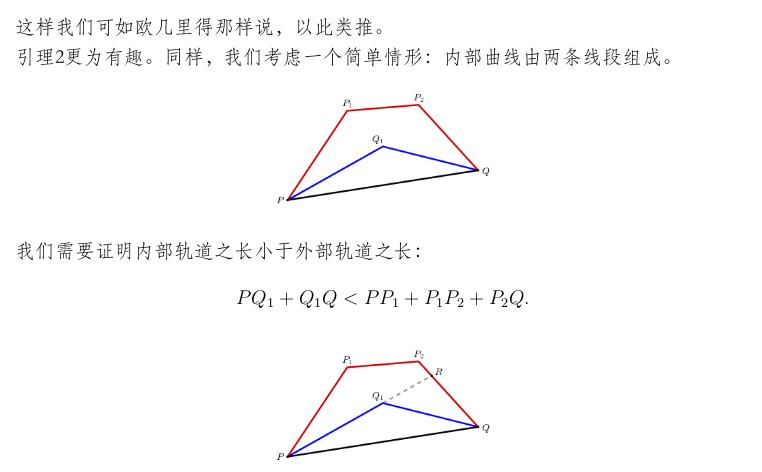
定义弧长

那要是不承认这两个关于曲线长度的引理呢？

如果不承认的话，那就无法在几何直观上比较曲线的长度（弧长）了。如果长度都不能比较，那么长度又有什么意义呢？

所以，如果不承认的话，就必须定义谁长谁短，换句话说，就必须严格定义曲线的长度。如果使用微积分中的曲线长度定义（折线长度的极限），那么再由此定义弧度后极限 \\(\\lim_\\limits{x \\to 0}\\frac{sin{x}}{x}=1\\) 就不证自明，推出圆的面积公式也就不能成为问题。而且如果这样定义曲线的长度，不需要 \\(\\lim_\\limits{x \\to 0}\\frac{sin{x}}{x}=1\\) 这一结论即可证明圆的面积公式：

根据微积分中对曲线长度的定义，可得出光滑曲线的长度等于下面的定积分：

\\( \\int_{a}^{b}\\sqrt{[x\'(t)]^2+[y\'(t)]^2}\\mathrm{d}t \\)

由此可得圆的周长为

\\( c = 4\\int_{0}^{r}\\sqrt{1+(\\frac{\\mathrm{d} }{\\mathrm{d} x}\\sqrt{r^2-x^2})^2}\\;\\mathrm{d}x \\)

\\( = 4\\int_{0}^{r}\\frac{r}{\\sqrt{r^2-x^2}}\\mathrm{d}x \\)

由此可得，圆的周长与半径成正比（符合几何直观），并定义单位圆的周长为 \\(2\\pi\\). 由此得 \\( c = 2\\pi r \\)

又因为圆的面积为 \\( s = 4\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x \\)

所以要证的圆的面积公式等价于

\\( 2s = rc \\)

\\( \\Leftrightarrow 2\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=r\\int_{0}^{r}\\frac{r}{\\sqrt{r^2-x^2}}\\;\\mathrm{d}x \\)

\\( \\Leftrightarrow 2\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=\\int_{0}^{r}\\frac{r^2}{\\sqrt{r^2-x^2}}\\;\\mathrm{d}x \\)

\\( \\Leftrightarrow 2\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=\\int_{0}^{r}\\frac{(r^2-x^2)+x^2}{\\sqrt{r^2-x^2}}\\;\\mathrm{d}x \\)

\\( \\Leftrightarrow 2\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=\\int_{0}^{r}\\frac{r^2-x^2}{\\sqrt{r^2-x^2}}\\;\\mathrm{d}x+\\int_{0}^{r}\\frac{x^2}{\\sqrt{r^2-x^2}}\\;\\mathrm{d}x \\)

\\( \\Leftrightarrow 2\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x-\\int_{0}^{r}x\\cdot\\frac{-x}{\\sqrt{r^2-x^2}}\\;\\mathrm{d}x \\)

\\( \\Leftrightarrow \\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=-\\int_{0}^{r}x\\cdot\\;\\mathrm{d}(\\sqrt{r^2-x^2}) \\)

\\( \\Leftrightarrow \\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=-\\left [(x\\sqrt{r^2-x^2})\\bigg\\rvert _{0}^{r}-\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x\\right ] \\)

\\( \\Leftrightarrow \\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=-\\left [0-\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x\\right ] \\)

\\( \\Leftrightarrow \\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x=\\int_{0}^{r}\\sqrt{r^2-x^2}\\;\\mathrm{d}x \\)

得证。

不用积分

说来说去都是积分，能不能不用积分？能不能不用繁琐的曲线长度定义？

当然可以。退而求其次，我们可以只定义圆弧的长度，并使这个定义能放到一般曲线长度定义的框架之内。而且上文提到，阿基米德就没用积分（那个时代根本就没有积分这种东西）。但他的方法有点麻烦（见上文提到的那篇论文）。这里结合刘徽的方法，给出一个更简单的证明。虽然没用积分，但也用到了极限的概念和性质。

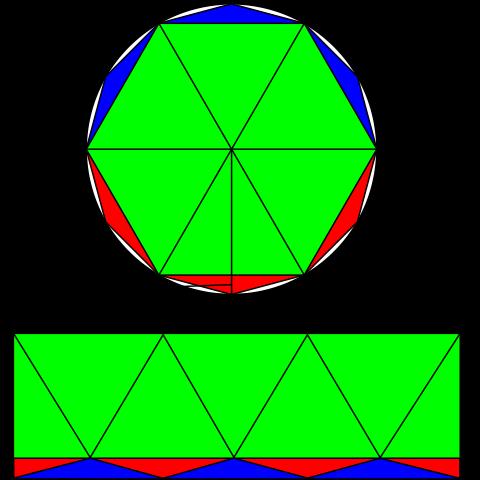
（图片来自 Wikipedia, 实在懒得画图了）

先定义圆弧长，求出周长。

作出圆的内接正 \\( 6\\cdot 2^n \\) 边形。易知该多边形的周长随 \\(n\\) 严格单增（图中红色和蓝色的三角形的两腰之和大于底边长）。又因为内接正多边形的周长一定小于任何一个外接正多边形的周长（对折线应用阿基米德引理），所以由单调有界收敛定理知，\\(n\\) 趋近于无穷时，内接正多边形的周长必收敛。定义内接正多边形周长的极限为圆的周长。由此得圆的周长和半径成正比。定义半径为 \\(\\frac{1}{2}\\) 的圆的周长为 \\(\\pi\\).

再证圆内接正多边形的面积收敛于圆的面积，然后利用已求出的周长和极限的惟一性求出圆的面积。

设半径为 \\(r\\) 的圆的面积为 \\(S\\), 内接正 \\( 6\\cdot 2^n \\) 边形的边长为 \\(L_n\\), 面积为 \\(S_n\\). 由定义知 \\(\\lim_\\limits{n\\to\\infty}L_n=2\\pi r\\). 设 \\(\\Delta_n = S_n - S\\). 作出该圆的内接正 \\( 6\\cdot 2^n \\) 边形和内接正 \\( 6\\cdot 2^{n+1} \\) 边形。考察 \\(\\Delta_{n+1} \\) 和 \\( \\Delta_n \\) 的关系。不妨设图中绿色部分为圆内接正 \\( 6\\cdot 2^n \\) 边形。观察图中长方形 \\(ABCD\\) 可知

\\( 6 \\cdot 2^n \\cdot S_{ABCD} > \\Delta_n \\)

\\( 6 \\cdot 2^n \\cdot \\frac{1}{2}S_{ABCD} > \\frac{1}{2}\\Delta_n \\)

\\( S_{n+1}-S_n > \\frac{1}{2}\\Delta_n \\)

\\( \\Delta_n - \\Delta_{n+1} > \\frac{1}{2}\\Delta_n \\)

\\( \\Delta_{n+1} < \\frac{1}{2}\\Delta_n \\)

 由此得

\\( \\Delta_{m+p} < \\frac{1}{2^p}\\Delta_m \\)

\\( \\Delta_{n+1} < \\frac{1}{2^{n}}\\Delta_1 \\)

\\( \\Delta_n < \\frac{1}{2^{n-1}}\\Delta_1 \\;\\; (n \\geqslant 2) \\)

因为 \\( \\frac{1}{2^{n-1}}\\Delta_1 \\) 当 \\(n\\) 足够大时可以任意小，所以 \\( \\Delta_n \\) 可以任意小，所以 \\( \\lim_\\limits{n\\to\\infty}S_n = S \\).

又因为 \\( S_n=\\frac{1}{2}h\\cdot L_n = \\frac{1}{2}r(\\cos{\\frac{180^{\\circ}}{2^n}})\\cdot L_n \\)

所以 \\( \\lim_\\limits{n->\\infty}S_n = \\frac{1}{2}r\\cdot 2\\pi r = \\pi r^2 \\)

又由极限的惟一性知 \\( S = \\pi r^2 \\).

证毕。

结论

圆的面积公式反映的是圆的面积与周长的关系，因此圆上的弧长不能是模糊不清的概念。

满足以下两个条件之一，便可严格证明圆的面积公式：

一、承认几何直观上比较弧长和直线与折线长度的两个结论

二、严格定义弧长

最后扯淡

第一次发现教材里有这个循环论证并得到确认后我还是很震惊的。数学教材怎么会出这么大一个漏洞？虽然涉及几何直观的地方，因为几何本身就不严谨，所以有一点不严格也无伤大雅，但是这么一个大问题在那里，教材一句话也不说就默认没问题了，总有种蒙混过关的感觉。好歹加个注说明一下。

后来我一直在想，出现这种问题的根本原因是什么。我觉得主要有以下两点：

一、这群编书的人根本就不重视几何

二、基础定理的证明都是抄来抄去，没有人考虑其他的证明方法

其实 \\(\\lim_\\limits{x \\to 0}\\frac{\\sin{x}}{x}=1\\) 这个式子说了一件什么事？无非就是「弦长趋近于弧长」。但是很多人不是这样想的。他们去用定义推导正弦函数的导函数，然后发现需要求这个极限，就去（用代数的方法）求了，完全没有去考虑这个极限的几何意义是什么。结果推导的时候发现代数上需要那个不等式，不得不又回到几何，再然后就出了循环论证这档子事。不仅如此，他们从一开始求导的时候就把几何给放到一边去了。讲真，从几何的观点来看，\\( \\frac{\\mathrm{d}}{\\mathrm{d} x} \\sin x = \\cos x \\) 和 \\( \\frac{\\mathrm{d}}{\\mathrm{d} x} \\cos x = - \\sin x \\) 简直不能再显然了：

如图，假设有一质点在单位圆上以 1 rad/s 做匀速圆周运动，座标（位置矢量）是 \\( (\\cos t, \\sin t) \\), 那么显然，它的速度就是 \\( (\\cos (t+90^{\\circ}), \\sin (t+90^{\\circ})) = (-\\sin t, \\cos t) \\), 把 \\(x\\) 轴和 \\(y\\) 轴的分运动拿出来就得到了正弦和余弦的导数。

所以说几何的东西就应该从几何的角度来思考，傻傻地去硬算就容易走入歧途。