统计学习主成分分析PCA(Princple Component Analysis)从原理到实现
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了统计学习主成分分析PCA(Princple Component Analysis)从原理到实现相关的知识,希望对你有一定的参考价值。
【引言】--PCA降维的作用
面对海量的、多维(可能有成百上千维)的数据,我们应该如何高效去除某些维度间相关的信息,保留对我们“有用”的信息,这是个问题。
PCA给出了我们一种解决方案和思路。
PCA给我的第一印象就是去相关,这和数据(图像、语音)压缩的想法是一致的。当然,PCA像是一种有损的压缩算法。但是不要紧,去除掉的信息也许是噪声呢,而且损失的信息不是“主要成分”。
PCA 降维的概念不是简单的去除原特征空间的某些维度,而是找出原特征空间的新的正交基,并且这个新的特征空间在某些唯度上信息量很少,可以忽略。使用这些新的正交基,我们可以表示出新的特征空间,。
【实例】--从二维的降维解释(高维空间的降维问题也是一样的思路,这里注意样本的上下标表示:上标表示第几个样本,下标表示第几维的特征;所有向量都是列向量表示)
问题描述:
现在有数据集m个样本
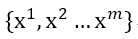
每个样本是一个二维特征空间的点(维度n=2)
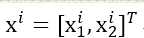
现在我们希望,找出新的正交基u1和u2(n维空间使用n个正交基就可以),重新表示这个空间(这个十分有趣,类似于矩阵乘法的物理意义:对向量做了线性变换),并且使得所有特征点在某些正交基(某些维度)上分量(类似于所有特征点对应的特征向量在该正交基上的投影之和)比较多(主成分由此而来),这样我们可以认为在该维度上
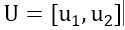
解决方案:
(1)假设数据已经零均值化(这个只是为了方便运算,提前零均值化)
如果这二维的可视图来看,我们人类很容易就知道了下图的u1信息较多。为何我们这么认为呢?怎么数字化的表示这个求U的过程。
我们可以认为所有特征点在u1方向上的投影之和比较大,u1可以作为正交基。这样u2方向上的投影之和比较小,说明在u2方向上数据的不确定性比较小,基本在很小的范围内波动,甚至可以把这种波动当作噪声,可以认为在该方向上分量为0。
这里用了数据的不确定性和波动,感觉还是比较形象的。由波动,引申出统计学的方差(方差刚好就是衡量数据相对于均值波动的),实际上我们就是在找波动最大,不确定最大的方向作为新的正交基。这就时最大方差理论的由来,不够在证明上,尽量使用“投影之和的概念”。
求U的过程这类似一个求极值的过程,找到u1使得所有特征点在u1上投影之和最大,依次找出u2...最终得到U
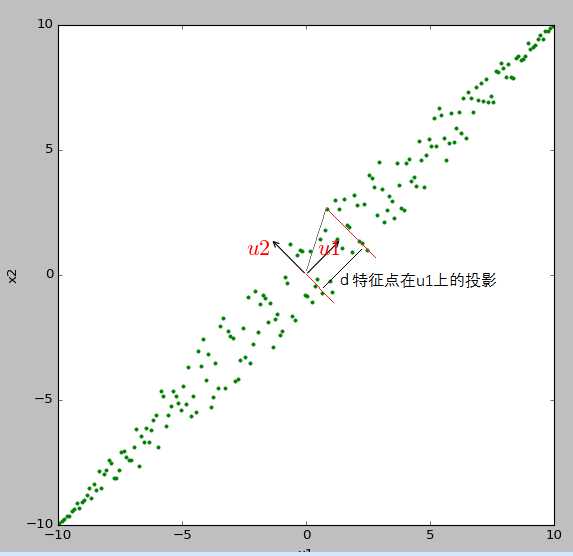
(2)投影之和
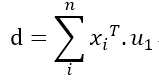
这里使用了向量的点乘的物理意义:投影,刚好u1是单位向量。xi是原特征空间某一维度的所有取值,即xi是一个m维的向量,每个分量都是一个样本在唯度i上的样本值。
我们稍微修改下d,更方便计算。
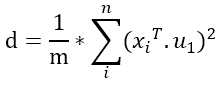
a.对该公式做下变化:

note1:一点都不显然,其实
b.原始问题数学化
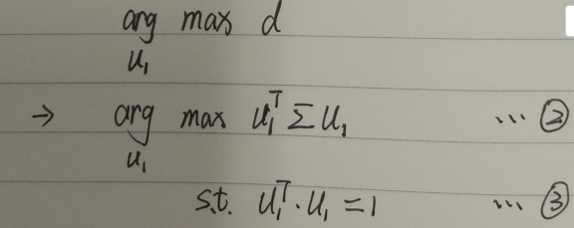
note3: 单位正交基的性质
c.使用拉格朗日求解约束问题
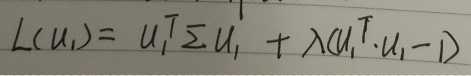
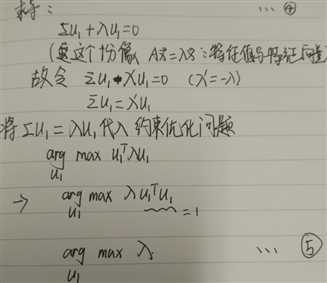
note4:对向量求导比较难以理解。
(3)最后问题归结为:求协方差矩阵的最大特征值及对应特征向量(刚好就是新的正交基),此时该正交基上的信息量(不确定性)最大。--note5
所以主成分可以通过求特征值及求特征向量来分析。特征值大,在对应特征向量的投影之和或者波动大。我们只需保留特征值较大的特征向量即可
(4)得到低维的数据
a.如何实现正交基的变换(联系矩阵乘法)
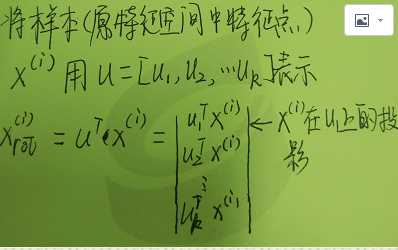
b.对上式做转置
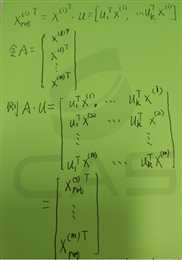
于是A*U就是低维空间的数据,维度为k.
【实现】
实现比较简单,基本是证明的思路一步步求解即可
1 #encoding: UTF-8 2 ‘‘‘ 3 Created on 2016??12??14?? 4 5 @author: YYH 6 ‘‘‘ 7 import numpy as np 8 from array import array 9 # 自己实现参考 10 # http://blog.csdn.net/u012162613/article/details/42177327 11 # 传入的数据格式: array 12 # 每一行代表一个样本 13 # 每一列代表一个唯度的信息 14 15 #数据中心化,使得各个维度的信息均为0 16 def meanshift(dataArr): 17 mean = np.mean(dataArr,axis=0)#对每一列求均值 18 newData = dataArr-mean 19 return newData,mean 20 def zeroData(dataArr,mean): 21 newData = dataArr-mean 22 return newData 23 class PCA: 24 def __init__(self, n_components=1,percentage=0.99): 25 self.dstDim = n_components 26 self.reservePercentage = percentage 27 28 def __del__(self): 29 pass 30 def fit(self,dataArr): 31 zeroMeanData,meanVal = meanshift(dataArr) 32 self.meanVal = meanVal#保存数据中心 33 # 求协方差矩阵,rowvar = 0:一行代表一个样本 34 cov = np.cov(zeroMeanData,rowvar=0) 35 #求特征值和特征向量,特征向量是按列放的,即一列代表一个特征向量 36 eigVals,eigVector =np.linalg.eig(cov) 37 38 eigValsIndice = np.argsort(eigVals)#从小到大排列 39 n_eigValsIndice = eigValsIndice[-1:-(self.dstDim+1):-1] #最大的n个特征的下标 40 41 n_eigVect = eigVector[:,n_eigValsIndice]#最大的n个特征值对应的特征向量 42 n_eigVect = np.matrix(n_eigVect) 43 self.n_eigVect = n_eigVect #保存特征向量 44 45 def fit_transform(self,dataArr): 46 zeroMeanData,meanVal = meanshift(dataArr) 47 self.meanVal = meanVal#保存数据中心 48 # 求协方差矩阵,rowvar = 0:一行代表一个样本 49 cov = np.cov(zeroMeanData,rowvar=0) 50 #求特征值和特征向量,特征向量是按列放的,即一列代表一个特征向量 51 eigVals,eigVector =np.linalg.eig(cov) 52 53 eigValsIndice = np.argsort(eigVals)#从小到大排列 54 n_eigValsIndice = eigValsIndice[-1:-(self.dstDim+1):-1] #最大的n个特征的下标 55 n_eigVect = eigVector[:,n_eigValsIndice]#最大的n个特征值对应的特征向量 56 57 zeroMeanData = np.matrix(zeroMeanData) 58 n_eigVect = np.matrix(n_eigVect) 59 self.n_eigVect = n_eigVect #保存特征向量 60 lowDData = zeroMeanData*n_eigVect #低维特征空间的数据 61 # reConData = (lowDData*n_eigVect.T)+meanVal #重构数据 62 return lowDData 63 def transform(self,dataArr): 64 zeroMeanData = zeroData(dataArr,self.meanVal) 65 zeroMeanData = np.matrix(zeroMeanData) 66 lowDData = zeroMeanData*self.n_eigVect #低维特征空间的数据 67 # reConData = (lowDData*n_eigVect.T)+meanVal #重构数据 68 return lowDData 69
【代码验证】
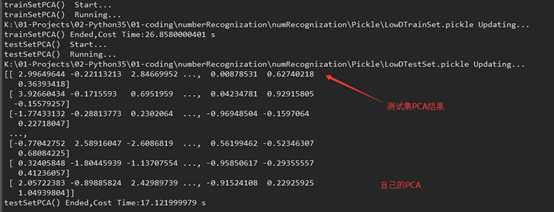
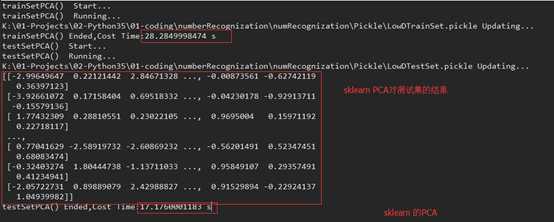
在做手写数字识别时,我分别使用了sklearn的PCA,和自己整理的PCA,达到的准确度都到了96%左右。
在PCA降维后的数据来看,可能在特征向量上方向不同,导致部分列跟sklearn的符号相反
时间上,可能自己整理实现的PC A现在耗时短点,毕竟目前是比较简单的PC A
【参考链接】
1.PCA 的最大方差理论和最小二乘法证明(PCA的概念讲得很清楚 但证明比较晦涩,不知道在作甚)
2.手把手交你实现PCA
3.Andrew Ng(通常不方差归一化)
4.PCA 证明(协方差的主特征向量就是数据变化最大的主方向)
5.LDA和PC A的证明
以上是关于统计学习主成分分析PCA(Princple Component Analysis)从原理到实现的主要内容,如果未能解决你的问题,请参考以下文章