欧拉公式的三种形式

Posted 2023-03-26

参考技术A

欧拉公式的三种形式如下：R+V-E=2，在任何一个规则球面地图上，用R记区域个数，V记顶点个数，E记边界个数，则R+V-E=2，这就是欧拉定理，它于1640年由Descartes首先给出证明，后来Euler于1752年又独立地给出证明，我们称其为欧拉定理，在国外也有人称其为Descartes定理。

欧拉公式又称为欧拉定理，也称为尤拉公式，是用在复分析领域的公式，欧拉公式将三角函数与复数指数函数相关联，之所以叫作欧拉公式，那是因为欧拉公式是由莱昂哈德·欧拉提出来的，所以用他的名字进行了命名。 

尤拉公式提出，对任意实数 x，都存在其中 e是自然对数的底数， i是虚数单位，而  \\cos和  \\sin则是余弦、正弦对应的三角函数，参数 x则以弧度为单位。这一复数指数函数有时还写作 cis(x)。由于该公式在 x为复数时仍然成立，所以也有人将这一更通用的版本称为尤拉公式。

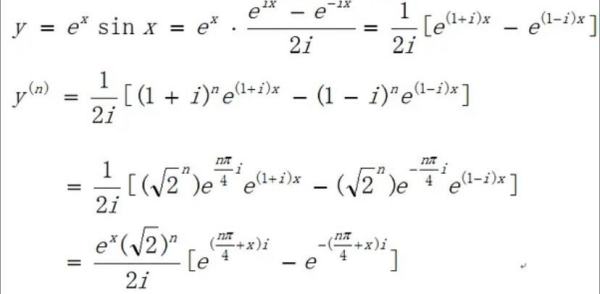
为什么欧拉公式被称为世界上最完美的公式了？

欧拉公式的巧妙之处在于，它没有任何多余的内容，将数学中最基本的e、i、π放在了同一个式子中，同时加入了数学也是哲学中最重要的0和1，再以简单的加号相连。高斯曾经说：“一个人第一次看到这个公式而不感到它的魅力，他不可能成为数学家。” 虽然不敢肯定她是世界上“最伟大公式"，但是可以肯定它是最完美的数学公式之一。

世界上最伟大的公式:欧拉公式(道尽数学的美好)

参考技术A

欧拉 公式 是世界上最伟大的 公式 、最完美的公式，被誉上帝公式。将e、π、i、乘法单位元1、加法单位元0这五个重要的数学元素囊括其中，在数学爱好者眼里，一言道尽了数学的美好。那么欧拉公式怎么来的?欧拉公式是什么?欧拉公式有什么用?下面就为大家带来详细介绍。

世界上最伟大的公式，欧拉公式

欧拉公式：R+ V- E= 2

在任何一个规则球面地图上，用R记区域个数，V记顶点个数，E记边界个数，则 R+ V- E= 2，这就是欧拉定理。1640年由Descartes(笛卡尔)首先给出证明，1752年Euler(欧拉)又独立地给出证明，因此我们将它叫做欧拉公式。有人问欧拉公式英语怎么说?英语是Euler's formula。

莱昂哈德·欧拉

欧拉公式的证明这欧拉是瑞士数学家、自然科学家。是18世纪数学界最杰出的人物之一，他不但为数学界作出贡献，更把整个数学推至物理的领域。他是数学史上最多产的数学家，还写了大量的力学、分析学、几何学、变分法等的课本。许多都成为了数学界中的经典著作。此外欧拉还涉及建筑学、弹道学、航海学等领域。

欧拉公式的意义是什么

许多人可能不了解，既然欧拉公式被誉为上帝公式，最完美的公式，那么它的意义是什么呢?想要知道欧拉公式的意义，首先我们需要清除它的证明和推导。

欧拉公式的证明

1、当 R= 2时 ，由说明 1,这两个区域可想象为 以赤道为边界的两个半球面 ，赤道上有两个“顶点” 将赤道分成两条“边界”，即 R= 2，V= 2，E= 2;于是 R+ V- E= 2,欧拉定理成立.。

2、设 R= m(m≥ 2)时欧拉定理成立，下面证明 R= m+ 1时欧拉定理也成立 。

由说明 2，我们在 R= m+ 1的地图上任选一个 区域 X ,则 X 必有与它如此相邻的区域Y ，使得在去掉 X 和 Y 之间的唯一一条边界后，地图上只有m 个区域了;在去掉 X 和 Y 之间的边界后，若原该边界两端 的顶点现在都还是3条或3条以上边界的顶点，则该顶点保留，同时其他的边界数不变;若原该边界一端或两端的顶点现在成为2条边界的顶点，则去掉该顶点，该顶点两边的两条边界便成为一条边界 。于 是 ,在去掉 X 和 Y之间的唯一一条边界时只有三种情况：

①减少一个区域和一条边界;

②减少一个区域、一个顶点和两条边界;

③减少一个区域、两个顶点和三条边界;

即在去掉 X 和 Y 之间的边界时，不论何种情况都必定有“减少的区域数+减少的顶点数=减少的边界数”我们将上述过程反过来 (即将 X 和 Y之间去掉的边 界又照原样画上) ，就又成为R= m+ 1的地图了，在这一过程中必然是“增加的区域数+ 增加的顶点数= 增加的边界数”。

因此，若 R= m (m≥2)时欧拉定理成立，则 R= m+ 1时欧拉定理也成立.。

由1和2可知，对于任何正整数R≥2,欧拉定理成立。

欧拉公式的推导

这个恒等式也叫做欧拉公式，它是数学里最令人着迷的一个公式，它将数学里最重要的几个数字联系到了一起：两个超越数：自然对数的底e，圆周率π;两个单位：虚数单位i和自然数的单位1;以及被称为人类伟大发现之一的0。数学家们评价它是“上帝创造的公式”。

因此欧拉公式的意义不局限于数学，信号处理，它将能解释一些物理概念和规律。例如，光速，暗物质等。

改变世界的十个公式

1、欧拉公式

2、麦克斯韦方程组

3、牛顿第二定律

4、勾股定理

5、薛定谔方程

6、质能方程

7、德布罗意方程组

8、1+1=2

9、傅立叶变换

10、圆的周长公式

详细》》世界上最伟大的十个公式