背包九讲 && 题目
Posted stupid_one
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了背包九讲 && 题目相关的知识,希望对你有一定的参考价值。
★、背包求方案数的时候,多重背包是不行的,因为产生重复的背包会有多种情况。
★、背包记录路径的时候,其实是不行的,因为更新了12的最优解,如果它依赖于6这个背包,然后你后面改变了6这个背包,就GG
1、01背包问题。
tot:总背包空间,vall[i]:每件物品的价值,w[i]:每件物品的重量
http://acm.hdu.edu.cn/showproblem.php?pid=2602
01背包明显可以只写一维的,所以二维的就不写了。
关于为什么可以只写一维的呢?这就和你枚举的顺序有关了。从tot 枚举 到 w[i]。那么是优先更新dp[比较大的数]
而且是从dp[i - 1][]那里更新过来的。至于后面枚举小的背包容量的时候,较大的背包容量是用不了的了,所以这里就可以避免有重复使用的bug。确保都是从dp[i- 1]枚举过来。而这个顺序反转了的话,刚好的完全背包的最优解。这个后面再说

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> #include <assert.h> #define ios ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1e3 + 20; int dp[maxn]; int w[maxn], val[maxn]; void work() { memset(dp, 0, sizeof dp); int n, tot; scanf("%d%d", &n, &tot); for (int i = 1; i <= n; ++i) { scanf("%d", &val[i]); } for (int i = 1; i <= n; ++i) { scanf("%d", &w[i]); } for (int i = 1; i <= n; ++i) { for (int j = tot; j >= w[i]; --j) { dp[j] = max(dp[j], dp[j -w[i]] + val[i]); } } printf("%d\\n", dp[tot]); } int main() { #ifdef local freopen("data.txt", "r", stdin); // freopen("data.txt", "w", stdout); #endif int t; scanf("%d", &t); while (t--) work(); return 0; }
一个常数的优化:

我把tot加大到10000.然后提交就变成了655ms。下面来说说当总背包容量tot比较大的时候,该怎么优化。
对于第n件物品,我们的转移方程是dp[tot] = max(dp[tot], dp[tot - w[n]); //这个就是答案
其实只需要一步就够了,因为我们需要的是dp[tot],不用再向下枚举了。但是根据上面的代码,是需要枚举到
for (j := tot; j >= w[n]; --j),是需要枚举到w[n]的,为什么呢?其实是为了给后面的做铺垫。因为我们并不知道这个是最后的一个背包,所以还是需要枚举到w[i]的,因为后面的背包可能需要用到dp[w[i]]这个背包的值。来更新最优解
那么我们可以算出一个下限,什么下限呢,就是后面的所有可能的背包中,最多需要用到那一个背包。
对于最后一个背包,他只需要用到dp[tot - w[n]]这个背包就够了。枚举到倒数第二种物品的时候,
他只需要用到dp[tot - w[n] - w[n - 1]]这个背包就够了。那么前面的背包,我们就不需要更新了。
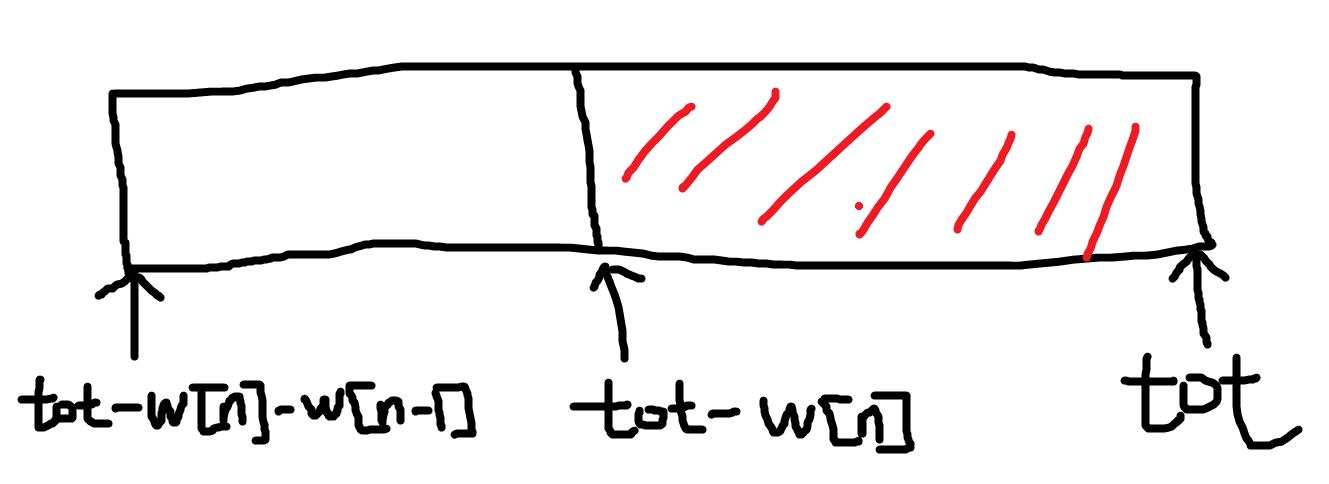
感觉还是写张图比较好理解,以免我以后忘记。
现在考虑枚举到了倒数第二种物品,我们只需要更新红色那个区域就行了,因为最后一个物品只需要用到dp[tot - w[n]]
那么同理,需要更新红色那段区域,我们只需要知道[tot - w[n] - w[n - 1], tot]这段区域的最优值是谁就可以了,因为我们为了更新红色那段区域,对于倒数第二种物品,其重量是w[i],下限就是tot - w[n] - w[i],故按照这个思路递推回去第i件物品即可。
这个用来优化当tot比较大的时候,是有用的,我把tot和w[]都同时加上了一个fix值,结果TLE,不是TLE就是RE。还是找到合适的题目再写上来吧,

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> #include <assert.h> #define IOS ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1e3 + 20; int dp[maxn]; int w[maxn], val[maxn]; int suffix_sum[maxn]; void work() { memset(dp, 0, sizeof dp); int n, tot; scanf("%d%d", &n, &tot); for (int i = 1; i <= n; ++i) { scanf("%d", &val[i]); } for (int i = 1; i <= n; ++i) { scanf("%d", &w[i]); } suffix_sum[n + 1] = 0; for (int i = n; i >= 1; --i) { suffix_sum[i] = w[i] + suffix_sum[i + 1]; } for (int i = 1; i <= n; ++i) { int toUpdate = max(w[i], tot - suffix_sum[i + 1]); for (int j = tot; j >= toUpdate; --j) { dp[j] = max(dp[j], dp[j -w[i]] + val[i]); } } printf("%d\\n", dp[tot]); } int main() { #ifdef local freopen("data.txt", "r", stdin); // freopen("data.txt", "w", stdout); #endif int t; scanf("%d", &t); while (t--) work(); return 0; }
关于dp的初始化。开始的时候dp[0] = 0表示容量为0的背包,能得到物品的价值是0.后面的就有两类了。
①、需要刚好装满tot个,那么,后面的就是全部都是-inf了,表示刚好刚好装满x个的时候,价值是负的,就是没有价值。
②、不需要的话,就全部都是0.
二维01背包,
POJ 1948
http://poj.org/problem?id=1948
给定n根木棒,要求全部用上,组成一个三角形,使得这个三角形的面积最大。
dp[i][j]表示组成的第一根木棒长度是i的时候,第二根木棒长度是j,第三根木棒的长度是dp[i][j]
那么对于周长是固定的话,那么dp数组开bool的就够了。dp[i][j] = 0表示这个方案不可行
比如dp[0][1] = true。表示第一根木棒是0,第二根木棒是1,第三根是all - 0 - 1。那么就全部木棒也用上了。
转移的话,if (dp[i][j]) then dp[i + val][j] = true; dp[i][j + val] = true;
就是这个物品,可以去两组中的任意一组,都可以。
同样也是枚举顺序的问题,应该倒着来枚举,因为木棒只能用一次。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> #include <assert.h> #define IOS ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1600 + 20; bool dp[maxn][maxn]; int a[maxn]; bool check (int a, int b, int c) { if (abs(a - b) >= c) return false; if (abs(a - c) >= b) return false; if (abs(b - c) >= a) return false; return true; } double calc(double a, double b, double c) { // cout << a << " " << b << " " << c << endl; double p = (a + b + c) / 2.0; // cout << p << endl; double ans = sqrt(p * (p - a) * (p - b) * (p - c)); return ans * 100; } void work() { int n; int all = 0; scanf("%d", &n); for (int i = 1; i <= n; ++i) { scanf("%d", &a[i]); all += a[i]; } // dp[0][0] = dp[a[1]][0] = dp[0][a[1]] = true; dp[0][0] = true; int en = (all + 1) / 2; for (int i = 1; i <= n; ++i) { for (int j = en; j >= 0; --j) { for (int k = en; k >= j; --k) { if (j >= a[i] && dp[j - a[i]][k]) { dp[j][k] = true; } if (k >= a[i] && dp[j][k - a[i]]) { dp[j][k] = true; } } } } int ans = -1; for (int i = 1; i <= en; ++i) { for (int j = i; j <= en; ++j) { if (dp[i][j] && check(i, j, all - i - j)) { ans = max(ans, (int)calc(i, j, all - i - j)); } } } printf("%d\\n", ans); } int main() { #ifdef local freopen("data.txt", "r", stdin); // freopen("data.txt", "w", stdout); #endif work(); return 0; }
一题比较好的,具有很强想象力的01背包问题。
题意就是在n个数中,选出一些数字,分成2组,使得两组的和是相同的,现在需要使得这个和最大。
那么可以dp[i][j]表示前i组数中,这两组东西的差值是j的时候,较大的那组数的和是dp[i][j]。那么dp[n][0]是答案
对于每一个物品a[i],为了产生差值为j时的方案。都有4种情况,
1、不选它,不要了, 那么dp[i][j] = dp[i - 1][j];
2、选择它放去比较矮的那组,那么这个时候,要产生差值是j,需要原本的差值是j + a[i]。而且这个时候,最高的那个值没变化。
3、放去较高的那组,那么这个时候,要产生差值是j,需要原本的差值是j - a[i],而且他变高了,所以是dp[i - 1][j - a[i]] + a[i]
4、放去较矮的那组,而且超越了本来较高的那组,然后现在的差值是j,这个需要画个图,
为什么会想到这4总情况
因为它是3大类。
1、不用
2、放了之后,最大高度不改变。
3、放了之后,最大高度改变
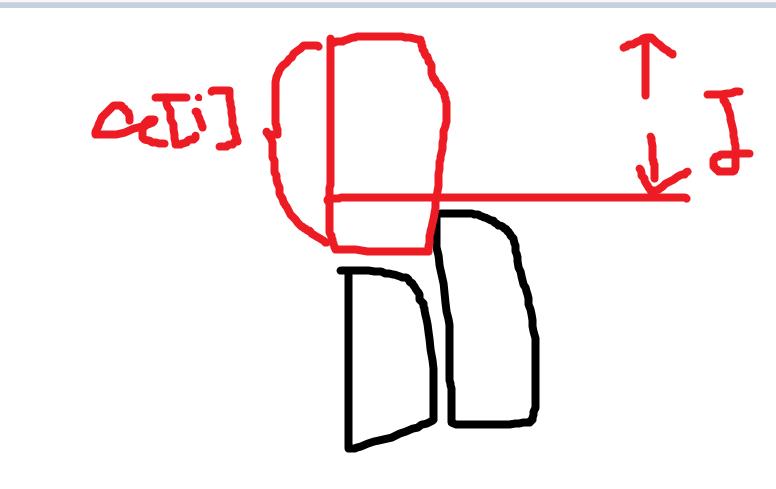
这时候是,由dp[i - 1][a[i] - j] + j转移过来。
然后取四个的最大值就好了。
这题不容易想啊。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> #include <assert.h> #define IOS ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 100 + 20; int a[maxn]; int dp[maxn][4000 + 20]; void work() { int n; cin >> n; for (int i = 1; i <= n; ++i) { cin >> a[i]; assert(a[i] >= 0); } memset(dp, -0x3f, sizeof dp); dp[0][0] = 0; for (int i = 1; i <= n; ++i) { for (int j = 0; j <= 2000; ++j) { if (j >= a[i]) { dp[i][j] = max(dp[i][j], dp[i - 1][j - a[i]] + a[i]); //放去高的 } if (a[i] >= j) { dp[i][j] = max(dp[i][j], dp[i - 1][a[i] - j] + j); } dp[i][j] = max(dp[i][j], dp[i - 1][j + a[i]]); //放在小的那里 dp[i][j] = max(dp[i][j], dp[i - 1][j]); //不用 } } if (dp[n][0] <= 0) { cout << "Impossible" << endl; } else cout << dp[n][0] << endl; } int main() { #ifdef local freopen("data.txt", "r", stdin); // freopen("data.txt", "w", stdout); #endif work(); return 0; }
new:

#include <bits/stdc++.h> #define IOS ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; int dp[100 + 2][4000 + 2]; void work() { memset(dp, -0x3f, sizeof dp); int n; scanf("%d", &n); int val; for (int i = 1; i <= n; ++i) { scanf("%d", &val); dp[i][val] = val; for (int j = 2000; j >= 0; --j) { dp[i][j] = max(dp[i][j], dp[i - 1][j]); if (j + val <= 2000) dp[i][j + val] = max(dp[i][j + val], dp[i - 1][j] + val); if (j >= val) { dp[i][j - val] = max(dp[i][j - val], dp[i - 1][j]); } else { dp[i][val - j] = max(dp[i][val - j], dp[i - 1][j] - j + val); } } } // printf("%d\\n", dp[2][3]); if (dp[n][0] <= 0) { printf("Impossible\\n"); } else printf("%d\\n", dp[n][0]); } int main() { #ifdef local freopen("data.txt", "r", stdin); // freopen("data.txt", "w", stdout); #endif work(); return 0; }
其实这题有一个很简单的方法的,
就是和上面的三角形一样,dp[i][j]表示第一座的高度是i,第二座的高度是j,是否可能。
唉,一开始怎么想不到,不过这个是水过去的,评测机快吧。870ms

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> #include <assert.h> #define IOS ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 100 + 20; int a[maxn]; bool dp[1000 + 20][1000 + 20]; void work() { int n; cin >> n; for (int i = 1; i <= n; ++i) { cin >> a[i]; assert(a[i] >= 0); } dp[0][0] = true; for (int i = 1; i <= n; ++i) { for (int j = 1000; j >= 0; --j) { for (int h = 1000; h >= 0; --h) { // dp[j][h] = dp[j][h] || dp[j - a[i]][h] || dp[j][h - a[i]]; if (j >= a[i]) { dp[j][h] = dp[j][h] || dp[j - a[i]][h]; } if (h >= a[i]) { dp[j][h] = dp[j][h] || dp[j][h - a[i]]; } } } } for (int i = 1000; i >= 1; --i) { if (dp[i][i]) { cout << i << endl; return; } } cout << "Impossible" << endl; } int main() { #ifdef local freopen("data.txt", "r", stdin); // freopen("data.txt", "w", stdout); #endif work(); return 0; }
还有这题也不错。 http://www.cnblogs.com/liuweimingcprogram/p/6238454.html
这就是一题暴力题,给定n组数字,每组数字能选出若干个,组成一个和值val。现在需要在这n组中,找出他们共有的和值。
明显对n组都做一次01背包,那么复杂度最坏1e8.但是我还是写了,居然127ms。
这里本来还想用一个常数的优化,但是是不行的,我要生成的是有多少个和值,而不是最优解。
dp[i][j]表示第i组,能否生成j这个和值。然后得到这个数组后,不应该用二分答案。因为有可能有些组没有这个值,然后有一个共同的更大的值。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> #include <assert.h> #define IOS ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1e2 + 20; bool dp[maxn][maxn * maxn]; vector<int>a[maxn]; int mx[maxn]; //int suffix_sum[maxn][maxn]; int n; bool check(int val) { for (int i = 1; i <= n; ++i) { if (!dp[i][val]) return false; } return true; } void work() { scanf("%d", &n); for (int i = 1; i <= n; ++i) { int x; int sum = 0; while (scanf("%d", &x)) { if (x == -1) break; a[i].push_back(x); sum += x; } mx[i] = sum; } // for (int i = 1; i <= n; ++i) { // for (int j = a[i].size() - 1; j >= 0; --j) { // suffix_sum[i][j] = suffix_sum[i][j + 1] + a[i][j]; // } // } for (int i = 0; i <= n; ++i) { dp[i][0] = true; } for (int i = 1; i <= n; ++i) { for (int j = 0; j < a[i].size(); ++j) { // int toUpdate = max(a[i][j], mx[i] - suffix_sum[i][j + 1]); for (int v = mx[i]; v >= a[i][j]; --v) { dp[i][v] = dp[i][v] || dp[i][v - a[i][j]]; } } } for (int i = 100 * 100; i >= 0; --i) { if (check(i)) { cout << i << endl; return; } } } int main() { #ifdef local freopen("data.txt", "r", stdin); // freopen("data.txt", "w", stdout); #endif work(); return 0; }
再来一题01背包,这个背包需要检查路径,而且需要检查是否合法。
感觉数据有点水,还不知道我的有没数据卡我的程序。
思路就是看看这n个数字中,有没有一些数字,和值是val。如果有多种情况,就输出-1,不可能,输出0.否则输出方案。
其实记录路径很简单的,这里不说了,主要是怎么确定他有多种解。
比如
18
6
1 2 3 4 5 6
这个是多种解的,3可以用1和2代替。
我的做法是把唯一解分成一组,另外的分成一组,然后两组再进行一次dp,如果能产生相同的数字,就不行,说明可以相互代替了。
dp[v].id,这个背包选了哪一个数字
dp[v].flag,这个背包可以由多少个背包转移过来。
dp[v].pre,这个背包的上一个背包。
说一说这里的小bug
3可以用1 +2代替,也可以用直接一个3来代替。我们选择1 + 2,然后记得标记已经生成了,就是3已经可以生成,不再去记录3的其他路径了。因为,还是上面那个例子。
在更新6的时候,18 = 6 + 12.是可以得。12在前面有被生成过。但是,它再次更新了12.12 = 6 + 6
这是不合法的,选了两次6了。所以,我们要记录唯一的路径。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> #include <assert.h> #define IOS ios::sync_with_stdio(false) using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> int a[111]; struct node { int id, pre; int flag; }dp[100 * 1000 + 20]; set<int>ans; vector<int>one; vector<int>two; bool out[100 * 1000 + 20]; bool visone[100 * 1000 + 20]; bool dpone[100 * 1000 + 20]; bool dptwo[100 * 1000 + 20]; void work() { int tot, n; cin >> tot >> n; for (int i = 1; i <= n; ++i) { cin >> a[i]; } dp[0].flag = 1; dp[0].id = dp[0].pre = inf; int tim = 0; for (int i = 1; i <= n; ++i) { for (int j = tot; j >= a[i]; --j) { if (dp[j].flag && dp[j - a[i]].flag) { dp[j].flag++;
