第二章:5.线性表应用---一元多项式的表示及相加
Posted AHAU航哥
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第二章:5.线性表应用---一元多项式的表示及相加相关的知识,希望对你有一定的参考价值。
前言:
学习了线性表的 顺序结构 和链式结构,那么这种学习有什么用?
本节将会学习如何用线性表来实现 一元多项式的表示及相加。
目录:
1.一元多项式
正文:
一元多项式:
数学上,一个一元多项式可写成 按幂升序排列的形式:
Pn(x)= P0 + P1x1 + P2x2 + .... + Pnxn
它由 n+1 个系数唯一确定,因此在计算机里可以用线性表 P 来表示:
P= (P0,P1, P2 , .... Pn);
其中每一项的指数 隐藏在Pi 的序号中
一元多项式的相加(采用 顺序存储结构):
设m<n ,两个多项式相加的结果为:Rn(x) = Pn(x) + Qm(x)
此运算可以用相性表R 来表示:
R= (P0 + Q0,P1+ Q1, P2 + Q2, .... + Pm+ Qm,Pm+1 ,.... Pn);
如果你已经掌握了 线性表的顺序存储,那么你会发现,显然R P Q 采用顺序存储结构,使得多项式的相加算法 十分简单清晰,很容易实现。
一元多项式的表示相加(采用 链式存储结构):
依然采用顺序结构来表示 一元多项式,那么对于如下多项式:
S(x)= 1 + 3x1000 + 2x20000
顺序存储结构会开辟 20001 个长度的存储空间,但是此多项式只有3项,于是造成了对内存空间的极大浪费。
改进:使用链式存储结构来表示 一元多项式,由于链式存储 数据元素在物理位置上不是相邻的,此时无法通过位序来确定 多项式中系数对应的指数,那么此时 链表只存储一元多项式的非零项,每个结点存储两个数据域:(项:pi ,指数:ei) 一个指针域:next。
这种形式下,最坏的存储情况是 多项式没有非零项,即 n+1 个项数,耗费存储空间为 采用顺序结构耗费存储空间 的2倍,但是对比 S(X)类型多项式的存在,一元多项式采用链表的形式将大大节省存储空间。
存储结构图示:
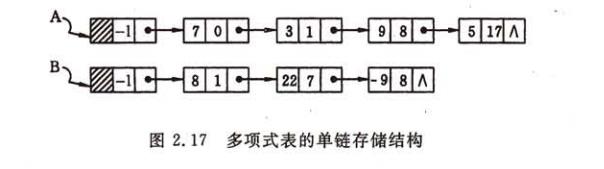
用C语言表示的存储结构:
typedef struct Polynomial{
float coef; //系数
int expn; //指数
struct LNode *next; //结点的指针域
}Polynomial,*LinkList;
代码实现:
#include<stdio.h>
#include<stdlib.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
//Status是函数的类型,其值是函数结果状态码
typedef int Status;
typedef struct Polynomial{
float coef; //系数
int expn; //指数
struct Polynomial *next; //结点的指针域
}Polynomial,*LinkList;
//创建具有m个项的一元多形式
Status CreatPolyn(LinkList &L,int m){
Polynomial * q=L; //q指向头结点(最后一个结点)
float coef;
int expn;
for(int i=0;i<m;i++){
printf("%s","请输入系数:");
scanf("%f",&coef);
printf("%s","请输入指数:");
scanf("%d",&expn);
Polynomial * Polyn=(LinkList)malloc(sizeof(Polynomial));
if(!Polyn) return ERROR;
Polyn->coef=coef;
Polyn->expn=expn;
q->next=Polyn; //追加结点
q=Polyn; //指向最后一个结点
}
q->next=NULL;
return OK;
}
//多项式Pa 和 Pb相加,将结果保存在Pa 链中。
void AddPolyn(LinkList &La,LinkList &Lb){
Polynomial * qa=La;
Polynomial * qb=Lb;
while(qa->next&&qb->next){
//1.如果当前 qa 的指数 大于 qb 的指数。那么把 qb 所指结点插入到qa 所指结点之后,
if((qa->next->expn)>(qb->next->expn)){
Polynomial * temp=qb->next;
qb->next=qb->next->next; //从 qb 中删除当前结点
temp->next=qa->next; //在 qa 当前元素前 插入 qb中删除的结点
qa->next=temp;
}
//2.如果当前 qa 的指数 小于 qb 的指数。那么只需后移 qa指针即可。
if((qa->next->expn)<(qb->next->expn)){
qa=qa->next;
}
//3.如果当前 qa 的指数 等于 qb 的指数。那么让对应系数相加。
if((qa->next->expn)==(qb->next->expn)){
float temp=(qa->next->coef)+(qb->next->coef);
//分别从qa 中删除当前结点
if(temp==0){
qa->next=qa->next->next;
}
//修改qa当前结点 的系数,后移指针。
if(temp!=0){
qa->next->coef=temp;
qa=qa->next;
}
qb=qb->next;
}
}
}
void PrintAllValues(LinkList &L){
Polynomial * q=L; //q指向头结点
while(q->next){
printf("系数:%f",q->next->coef);
printf("指数:%d\\n",q->next->expn);
q=q->next;
}
}
void main(){
Polynomial * Pa=(LinkList)malloc(sizeof(Polynomial));
Pa->next=NULL;
printf("%s\\n","Pa:");
CreatPolyn(Pa,4);
PrintAllValues(Pa);
Polynomial * Pb=(LinkList)malloc(sizeof(Polynomial));
Pb->next=NULL;
printf("\\n%s\\n","Pb:");
CreatPolyn(Pb,3);
PrintAllValues(Pb);
AddPolyn(Pa,Pb);
printf("\\n%s\\n","Pa+Pb:");
PrintAllValues(Pa);
}
运行结果:
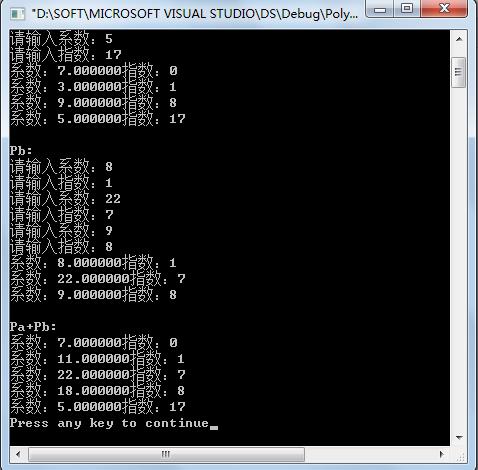
以上是关于第二章:5.线性表应用---一元多项式的表示及相加的主要内容,如果未能解决你的问题,请参考以下文章