序言
为了更好理解一些802.11的后续设计,我们需要深入了解一下802.11的协议性能。我们之前简单描述了下协议性能的部分,这一段我们讨论下具体数学模型下的802.11性能(Bianchi模型)。
Bianchi模型出自于论文《Performance Analysis of the IEEE 802.11 Distributed Coordination Function》,该论文在2000年的时候发表在JSAC(IEEE Journal on selected areas in communications)上,根据google scholar上的记录,该论文的他引次数已经高达8267次(相应的资源:bianchi模型)。其实关于802.11的理论性能从协议刚开始出来的时候就有人研究,直到现在,这个问题还是在继续研究中,该论文是这个领域中最为有代表性的一篇文章,故凡是做802.11协议的,都会阅读理解这篇文章。
PS:本文并不是按照Bianchi原文以推导的形式给出,而是为了方便理解进行的倒叙。其中部分表述和定义如果存在一些错误,还请见谅。
Bianchi模型的假设
我们首先列举一些Bianchi模型中,所设定的一些假设。
- Single-cell Network:可以简单认为是个单信道环境,即所有节点共享一个功能信道,并且这个网络中,所有的节点都是互相可以监听到对方的。
- The collision processes of the nodes can be decoupled:即无论节点重传了几次,其在传输时候的冲突概率都是一个定值,且都是相对独立的。
- Channel conditions are ideal:信道是一个理想信道,即传输错误仅仅由于传输碰撞造成,与物理层的信道质量无关。且由于Single-cell的假设,所有节点都可以互相监听,所以网络中也没有隐藏和暴露终端问题。
- Saturation throughput:Bianchi模型分析为饱和情况下的吞吐量,即任意一个节点都是假设有数据包的,不存在节点竞争到信道之后,没有数据包待发送的情况出现。
- No packet dropped:按照协议所述,如果数据包发送失败,节点是可以发起重传的。这个重传次数上限为6次,如果超过该次数,那么就需要丢包。而在Bianchi模型中,保留的重传次数上限为6次的这个设置,不过没有设定6次以后进行丢包,而是一直保持在第6次这个zhu
MAC层效率(归一化吞吐量)
在之前的一篇文章中,我们定义了MAC层的归一化吞吐量为传输真实数据(Data)的时间占总传输时间(Overhead + Data)的比例。
在Bianchi模型中,其具体定义如下(部分表述有稍微修饰一下)
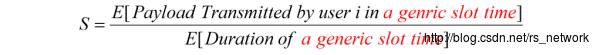
其中为归一化吞吐量(注:本文讨论的吞吐量都是系统的吞吐量,没有具体到某一个节点的吞吐量上,而是所有节点整体的吞吐量),分子分母都是一个数学期望,实际上就是平均时间。分母代表的是Generic slot(这个后面我们说明,与DCF中的标准slot时间存在区别),分子定义的是在这个Generic slot内,传输数据的时间。不严格的说,其物理意义和我们之前一篇描述的定义是一样的。
Generic Slot:这个是一个随机选择的时间,其与802.11中DCF的具体接入机制有关。一般意义上,我们理解其物理意义就是Backoff counter倒数1次的时间间隔。
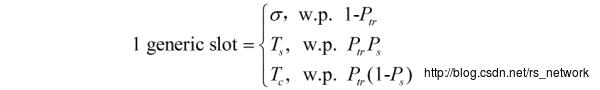
如上图为Generic slot的3种可能取值。其中代表协议中的slot时间(比如802.11g中的9μs),
为成功传输所花费的总时间,
为碰撞一次所花费的总时间。
为至少有一个节点准备发送的概率,
为成功传输的概率(实际上理解成只有1个节点传输的概率,如果有多个那么就会造成冲突)。我们进一步阐述如下:
- 情况1 —
:若节点在Backoff过程中,经过1个slot,backoff counter未倒数到0。这个概率为
,消耗的时间就是一个slot,即
时间。
若节点经过这个slot,backoff counter正好倒数到0,那么节点就会发送数据(即概率
- 情况2 -
:若节点成功发送该数据,那么损耗时间为
,其对应概率为
,即不仅发送,且发送成功。
- 情况3 -
:若节点发送数据,但是由于冲突(比如多个节点backoff counter倒数同时至0),那么这个数据帧是没有无法成功被接收的,这个损耗的时间就是
。其对应概率为
,即虽然发送,不过发送失败。
具体的
Basic模式:该模式的简单流程如下图:
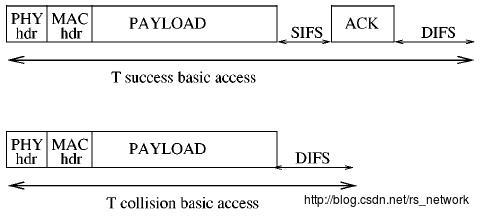
其中和
的时间如下:
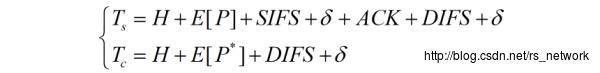
其中代表物理层头部的传输时间,
和
都是协议给定的帧间间隔,
为协议给定的ACK帧的传输时间,
为电磁波传播延迟(DATA-ACK过程由于是一来一回,所以传播延迟是两个)。
为payload的期望,代表数据包(MSDU)传输时间的均值。
代表的是发生冲突时,冲突中较长数据帧的均值,因为冲突只有在较长数据帧发送完之后,信道才被释放。
RTS/CTS模式:该模式的简单流程如下图:

其中和
的时间如下:
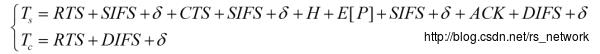
其中和
代表其数据帧对应的传输时间。上图中我们可以发现,RTS/CTS模式下,虽然传输时间是相应增加了(由于引入了RTS/CTS握手),但是冲突损耗是减少了。该设计能够保证,这个在节点较多的情况下(即碰撞概率较大的情况下),RTS/CTS的性能受到较小的影响。
本文为了简化,我们直接假设所有节点的数据包大小是一个定值,从而就等于传输这个数据包所花费的时间,且
。(在bianchi原文中没有进行该假设,只是为了简化本文的叙述,所以我们做数据包大小为定值的假设)
综合以上的Generic slot和其对应时间,我们可以具体给出归一化吞吐量的具体计算公式。
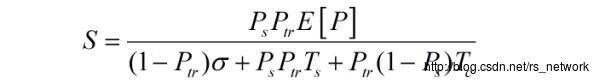
其中分母就是Generic slot的均值(即事件概率乘以其对应时间),分子为在一个Generic内,成功传输数据(MSDU)部分的时间。
传输概率( )和成功传输概率(
)和成功传输概率( )
)
前面我们给出了归一化吞吐量的表达式,该式中,由于
和
中的参数都是协议给定。为了计算吞吐量,我们只要求出概率
和
就行了。
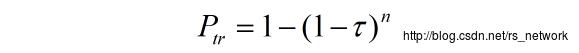
:其物理意义是至少有一个节点,在这个slot内准备传输。这里
指的是发送概率,
指的是总的竞争节点数目(由于假设是one-cell network,并且饱和吞吐量,所以所有节点都在竞争信道)。我们可以这样理解
的物理意义:
代表其中某
个节点没有发送的概率,
所有节点都没有发送的概率,所以其反面,
就是至少有
个节点可以发送的概率了。
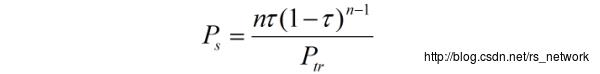
:这个实际上是个条件概率,物理意义是在有节点发送的前提下(即分母的
),成功传输的概率(即有且只有一个节点正在传输)。分子我们可以这样理解:
,其中
代表代表有
个节点正在发送,
代表其余
个节点都没有发送,即有且只有一个节点发送,那么才没有冲突。又是因为这个节点没有固定下来说,具体某一个节点,所以要做个排列组合,即一共
个节点,即
中情况,所以分子再乘以
。
上面我们介绍了和
的具体表达式,其中
是节点数目,所以一般也是给定的。所以最后剩下来的参数就是
了,我们需要对该参数进行分析。
发送概率( )和冲突概率(
)和冲突概率( )
)
通过以上分析,我们最终只要知道每一个节点的发送概率就可以求出吞吐量了,但是这个
就没有那么好求了,其主要是源于802.11协议中,发送和冲突是互相影响的。发送概率
中包含了冲突概率
,而冲突概率
中也包含了发送概率
。
以下我们描述一下bianchi模型中具体分析的过程。bianchi模型实际上采用了一个二维的Markov chain,具体如下图:
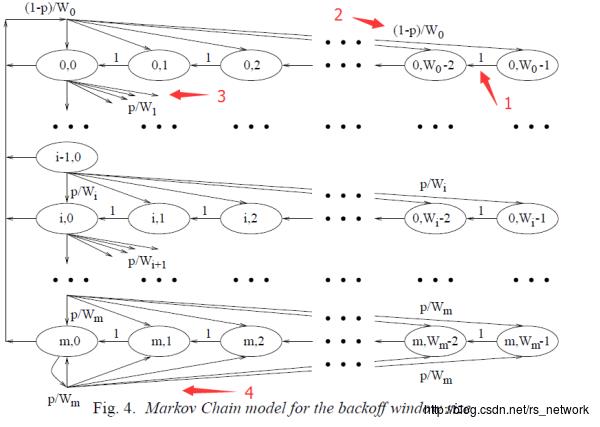
我们先简单说明下其中的一些参数,然后在具体讨论。每一横行代表的是一次Backoff过程,每一纵行代表的是一次二进制指数增加CW窗口大小的过程。以第1行为例说明如下:
- 状态
,
代表是第0次的Backoff过程(即CW窗口是默认大小),
代表Backoff counter选取数值为
(由于CW范围是从0开始,所以最大数值为
),
就是第0次Backoff时候的CW大小。
- 状态
转移至
代表了1次Backoff counter的回退(如图中红色1标识),其概率为
(因为不存在碰撞)。
- 当Backoff counter倒数至0后,即转移至状态
时,节点可以发送数据。
- 若发送成功(即概率
),如图中红色2标识,就需要重新在CW窗口内选择一个随机数(即某个随机数被选中的概率为
),并转移到该状态(比如转移到状态
,其转移概率为
)。
- 若发送失败(即概率
),如图中红色3标识,那么需要首先调节CW窗口大小(指数为2增长),即
变为
,在第二轮中,
。然后节点需要在更新后的CW窗口大小
中选择一个随机数(概率为
),并转移至该状态(比如转移到状态
,其转移概率为
)。
- 若发送成功(即概率
- 在Bianchi模型中,假设是没有丢包过程的。而二进制指数回退并不是上限无穷的增加CW窗口,其有个最大次数
次,在bianchi模型中。如果节点第m次回退后,还是发送失败,则不增加CW窗口大小,而是直接在这一轮设置的CW大小(
)中,直接选择一个随机数进行重传(这个概率就是
)。
更一般的我们用数学标识即是下面的式子:
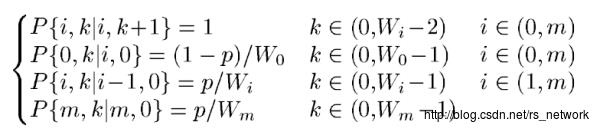
下面我们先表示冲突概率
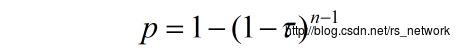
由于Bianchi模型中,已经假设节点之间的冲突过程是相对独立的。假设我现在是某个节点,我已经处于发送状态,所以剩余的个节点都不能够发送(即概率
),如果有任意一个也处于发送状态(即概率
),那么就会发生冲突。
最终我们考虑发送概率,参考下图
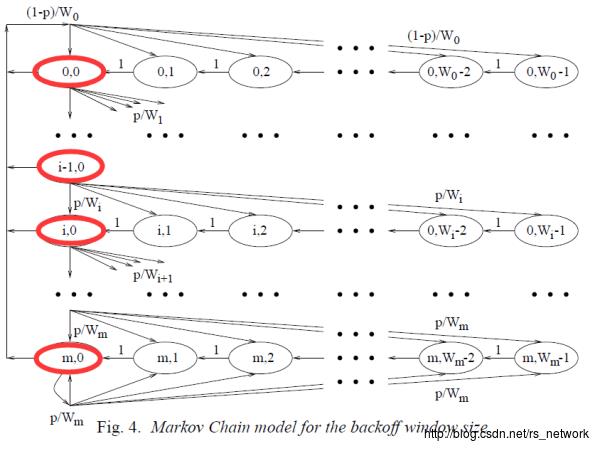
协议规定,如果节点Backoff counter倒数到0,那么就可以进行发送。由于节点可能处在不同的backoff状态(即初次传输,重传1次,重传2次等等),所以我们需要对转移到这些状态的概率做一个累加,即:
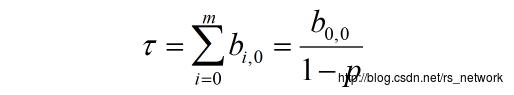
其中代表CW最多增加
次,
是个index,代表第
次Backoff过程,
代表状态,
代表第
次Backoff counter倒数到0。因为每一次发送完之后,节点都必须要转移到状态
。所以我们可以直接计算转移到状态
的条件概率。即如果发送没有发生冲突(即概率
),状态转移至
的概率(即
)。
最后我们表示出状态时候的稳态概率即可
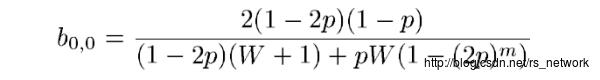
这个概率的物理意义有些繁杂,我们就不进行展开了,最终我们可以计算发送概率为:
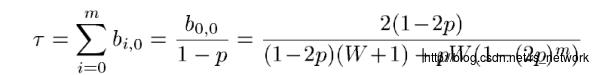
从而获得以下的一个联立的方程(其中上式的和下面的联立表达还有一个参数带入的步骤,具体可以参考论文,这里直接跳跃到下面的结果了):
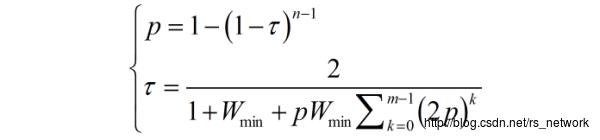
我们看到上面的表达中,表达式中包含
,同样
中表达式也包含
。故我们需要采用fix-point的方法,才可以对其进行求解。具体求解方法我们在下一篇文章中进行讨论。
结果分析
以下我们直接参考Bianchi论文中给出的结果,大致说明一下:
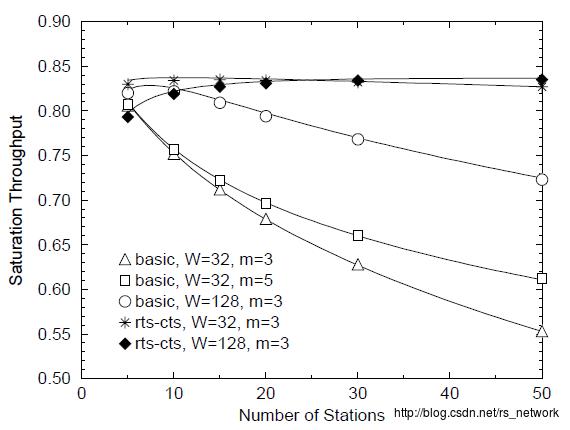
上图横轴代表节点数目(节点数目从0到50),纵轴代表归一化吞吐量(即范围从0~1,图中是从0.5开始绘制)。图中一共绘制5组结果:
代表Basic模式下,初始的CW窗口设置为32,CW窗口可以回退增大3次。
代表Basic模式下,初始的CW窗口设置为32,CW窗口可以回退增大5次。
代表Basic模式下,初始CW窗口设置为128,CW窗口可以回退增大3次。
从这三组值的对比上可以看出,节点数越多,Basic模式的性能越差。其基本原因就是冲突概率的增加。通过增加CW窗口大小的方法,能够一定程度上避免冲突问题,所以能够缓解随着节点数增加,而造成的吞吐量下降。初始设置更大的CW比增加回退次数要更有效一些。
代表RTS/CTS模式下,初始的CW窗口设置为32,CW窗口可以回退增大3次。
代表RTS/CTS模式下,初始的CW窗口设置为128,CW窗口可以回退增大3次。
在RTS/CTS模式下,可以发现其吞吐量相比Basic模式,能够在节点数较多的时候,受到较小的影响,其基本原因在于冲突损耗上。Basic模式冲突一次是损失了一个数据帧的时间,而RTS/CTS模式下,冲突一次仅仅损耗了一个RTS时间。同时我们还可以看到,由于冲突损失较小的情况下,我们没有必要设置更大的CW窗口大小,因为更大的窗口大小就意味着更多的回退次数,从而消耗更多的时间。