简单介绍神经网络算法

Posted 2023-03-25

参考技术A 直接简单介绍神经网络算法

神经元：它是神经网络的基本单元。神经元先获得输入，然后执行某些数学运算后，再产生一个输出。

神经元内输入 经历了3步数学运算，

先将两个输入乘以 权重 ：

权重 指某一因素或指标相对于某一事物的重要程度，其不同于一般的比重，体现的不仅仅是某一因素或指标所占的百分比，强调的是因素或指标的相对重要程度

x1→x1 × w1

x2→x2 × w2

把两个结果相加，加上一个 偏置 ：

（x1 × w1）+（x2 × w2）+ b

最后将它们经过 激活函数 处理得到输出：

y = f(x1 × w1 + x2 × w2 + b)

激活函数 的作用是将无限制的输入转换为可预测形式的输出。一种常用的激活函数是 sigmoid函数

sigmoid函数的输出 介于0和1，我们可以理解为它把 (−∞,+∞) 范围内的数压缩到 (0, 1)以内。正值越大输出越接近1，负向数值越大输出越接近0。

神经网络： 神经网络就是把一堆神经元连接在一起

隐藏层 是夹在输入输入层和输出层之间的部分，一个神经网络可以有多个隐藏层。

前馈 是指神经元的输入向前传递获得输出的过程

训练神经网络 ，其实这就是一个优化的过程，将损失最小化

损失 是判断训练神经网络的一个标准

可用 均方误差 定义损失

均方误差 是反映 估计量 与 被估计量 之间差异程度的一种度量。设t是根据子样确定的总体参数θ的一个估计量，(θ-t)2的 数学期望 ，称为估计量t的 均方误差 。它等于σ2+b2，其中σ2与b分别是t的 方差 与 偏倚 。

预测值 是由一系列网络权重和偏置计算出来的值

反向传播 是指向后计算偏导数的系统

正向传播算法 是由前往后进行的一个算法

深度学习之神经网络算法介绍

01 深度学习与神经网络算法

提到深度学习，大家的印象可能是这样的？

抑或是这样？

这些大部头的著作很容易给人艰深难懂的印象，使人望而却步。实际上，深度学习的入门还是很轻松简单的，今天，我就从深层神经网络(DNN)带你进入深度学习的海洋！

02 深度学习的应用

作为实现机器学习的一种技术，深度学习当然可以完成机器学习的各种任务，比如

→推荐系统（深层神经网络DNN的应用）

→图像识别（卷积神经网络CNN的应用）

→文字语义识别与机器翻译（循环神经网络RNN的应用）

当然，深度学习的应用如浩瀚星空，以上只是其中的小小一隅。而归结到底，DNN处理的还是分类任务。

分类任务指的是输入一个样本，其包含n个特性x1,x2,…xn,输出结果y。一个经典的例子是周志华老师的西瓜论，x1,x2,…xn代表西瓜的一些特性如颜色，瓜蒂，熟度等等，而 y代表这个西瓜是好瓜还是坏瓜。深度学习的任务就是用很多的样本训练之后，输入一个瓜的特性，判断这个瓜的好坏。

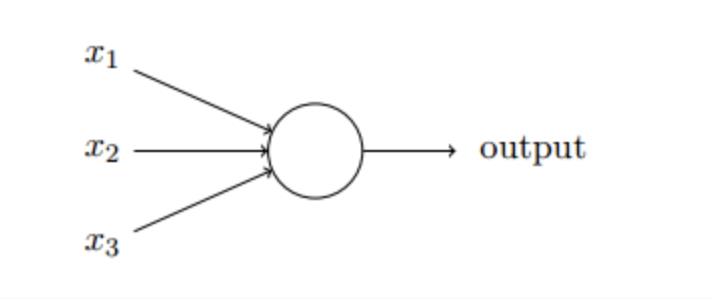
03 Logistic回归与多层神经网络

那么，要想了解神经网络是如何运作，而通过训练来作出判断的，我们就要从Logistic 回归，又称单层神经网络开始说起。

我们记一个训练样本x=[x1,x2,…xn] ，设置一个参数序列w=[w1,w2,…wn] , 采用线形回归函数 

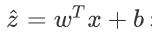
来输出结果, 但明显这个结果的值域很大，不符合我们分类问题的0或1的期望结果，我们就再采用sigmoid函数

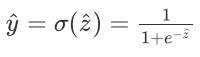
对其做进一步处理，如下图所示

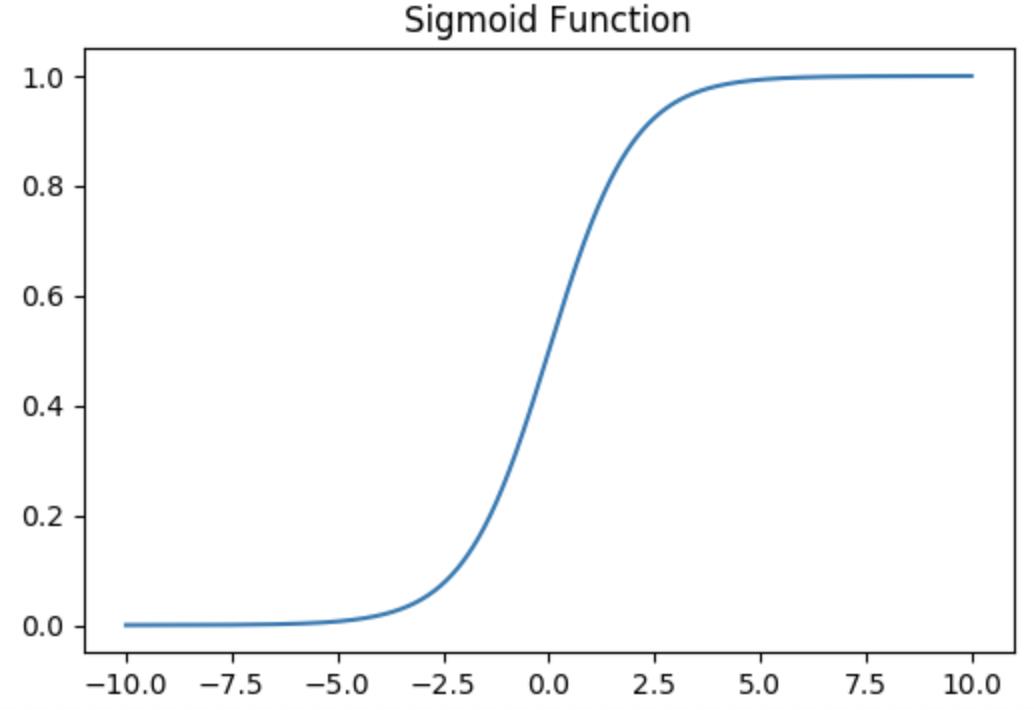
可以看到，这样y的估计值的值域就在[0,1]之间啦。

得到y的估计值后，我们再用下一节所介绍的梯度下降法将它与y的真实值比较，再在每一次训练中进行参数的调整，使得最终的参数符合最优的标准，即分类的结果与真实结果相差最小。

介绍完Logistic回归后，我们继续看多层向前神经网络。简而言之，多层神经网络就是多个Logistic回归的叠加：

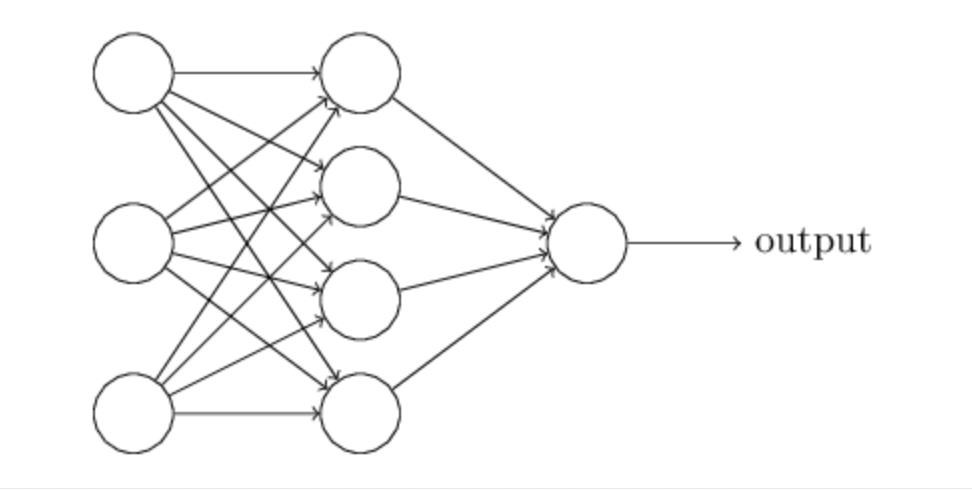
以上为两层神经网络，此时的W1(第一层参数)的size就不再是 n✖1了，而是n✖k, k为第二层神经元的个数。所以一个样本经过第一层神经网络之后为

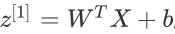
其size为

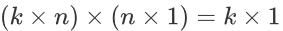
个，对于这k个神经元我们再采用类似于sigmoid的激活函数

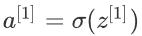
而后继续对a[1]进行相类似于第一层的处理就可以得到结果啦。

而多层神经网络与两层神经网络完全一致，只不过是层数增加，每层的参数会增加，其理解复杂度不会变化。

04 梯度下降法

了解了神经网络的前向传播之后，我们要学习的就是如何训练我们的参数W和b了。

此时我们定义一个损失函数(Loss Function): 

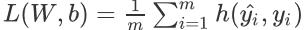
其中m为样本的个数，两个y相关的参数分别是y的估计值和真实值，且有

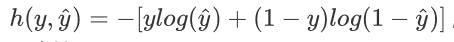
我们解释一下这个函数，当y=1时,y的估计值越接近于0，函数值整体越大；y=0时同理。

定义好损失函数之后，我们训练的目的就是使得损失函数最小，这当然是沿着梯度方向下降最好了。

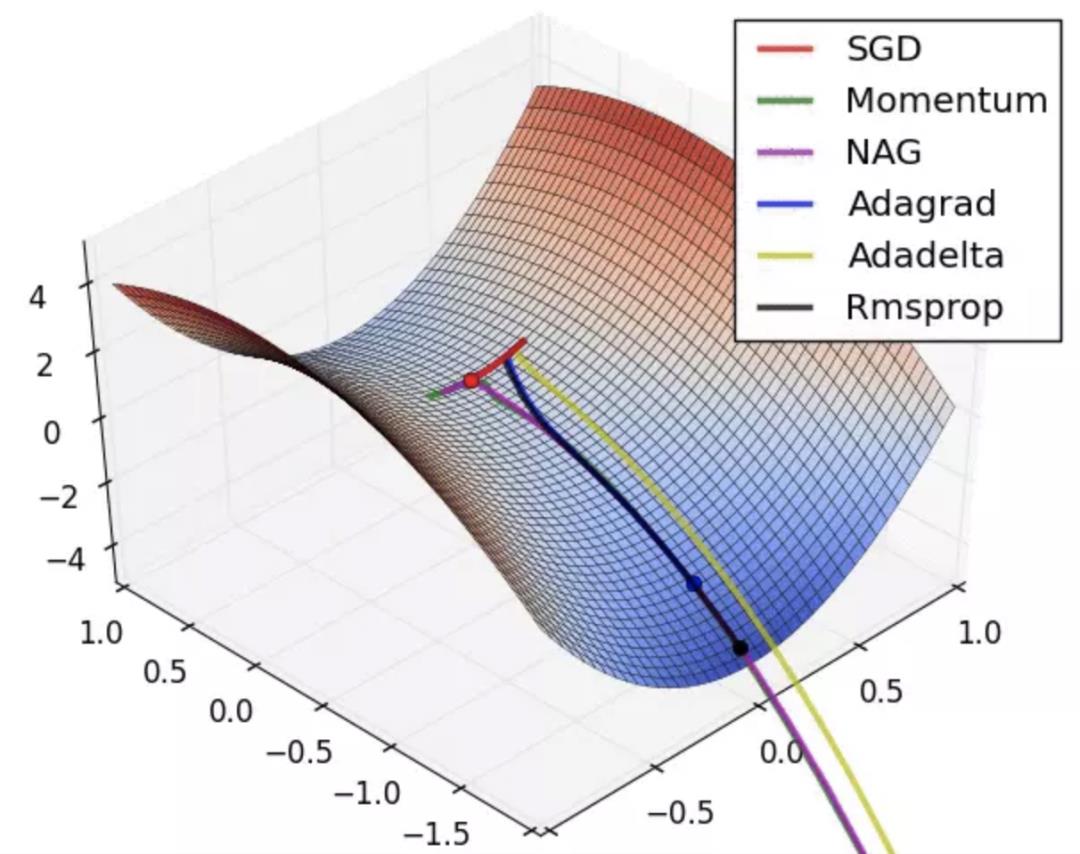
如上图所示，最快使得损失函数到达最低点的情况就是参数沿导数方向走，即

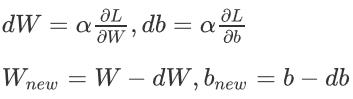
当样本足够多的时候，L 会下降到一个很低的值，这样我们的训练就完成了。

在文章的最后，小统想给大家带来一个思考题：一般来说大家提到损失，第一个蹦入脑海的应该是平方损失

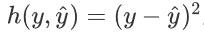
那么在神经网络与梯度下降法中为什么不用这个函数呢？

最后的最后，再给看到这里的大噶带来一个好消息——清华计算机学院自研的深度学习框架“计图”已经于近日开源啦！

其多项任务性能超过目前主流深度学习框架PyTorch，在机器视觉任务上性能甚至提高10%-50%，大家也可以去尝鲜啦！

浙大统计学人

文案：孙张诚

排版：林子跃