剩余定理

Posted 2023-03-25

我的数学方面只有高中的一般水平，麻烦有能力的大神能给小生一个浅显易懂的办法，谢谢！

我在你的另一处提问中答过此题。其中讲到了简化的计算方案。另外，我对mod符号给出了说明。建议你多加参考。
这时，我再用中国剩余定理，试图简要说明，力求易于理解。

一个数被5除余2,被6除少2,被7除少3,问这个数最小是多少？
注意：这里将题意理解为求最小正整数或自然数解。
解：
首先转化成：自然数x被5除余2,被6除余4,被7除余4,问这个数最小是多少
一：线性分解，必需的：
然后，假设将这个数分成三部分：x=x1+x2+x3
其中,
x1被5除余2,被6除余0,被7除余0,
x2被5除余0,被6除余4,被7除余0,
x3被5除余0,被6除余0,被7除余4,
这种剖析法，在数学上称为线性叠加。数论上的中国剩余定理，计算数学中的插值方法，基本上都是利用这一原理。多元一次方程组，也可以用这种思路来解，因此也称为线性方程组。此方法形成一门数学分支，称为线性代数，用向量与矩阵，可以大大简化问题的描述与思考过程。

在本答案的第四部分中，我用此思路计算出此题的答案。

二：单位的引进，并不是必要的
中国剩余定理呢，为了理论的简明与方便，是将问题分成了三个单位
先找到r1被5除余1,被6除余0, 被7除余0, 那么2*r1自然就是前面所讲的x1了。
同样，r2被5除余0,被6除余1,被7除余0, 那么4*r2自然就是前面所讲的x2了。
同样，r3被5除余0,被6除余0,被7除余1, 那么4*r3自然就是前面所讲的x3了。
这里的三个单位数组(1,0,0)，（0，1，0）， (0,0,1)便是单位向量。组成矩阵就是单位矩阵。
用单位数组来解决问题，具有统一性，但并不是必要的。用前面的思路来解，常常还会简化计算过程。所以我们理解了之后，对中国剩余定理不必太过拘泥。
另外，我们发现，中国剩余定理，也就是线性叠加的一个特例。当我们推而广之之后，发现，也并不神秘。

三：细节计算举例
注意：同余的理解，模的理解。如果理解了他的本质，我看，同余号与模概念的形式引进，并不是必需的。
子问题：
求r1,使得r1被5除余1,被6除余0, 被7除余0。
答：
显然，r1被6,7整除，从而被6,7的最小公倍数整除。
而6,7不可约，即互质(或称互素)，或说6,7的最大公约数为1,
于是他们的最小公倍数就是它们的乘积6*7.
于是可设
r1=6*7k1=1 (±5**)或1(+)5*() 。
会解这样的不定方程或后文讲到的同余式，那么你就可以解答同余式组问题，也就是出题人所提的一类问题了。后文注3专讲如何解答。

注1：
这时现有的较好的得化处理是引进同余记号。
r1=6*7k1==1 mod 5
不过，这并不是必需的。因为我们写成r1=6*7k1=1 (±5**)或1(+)5*() 也行。
这里与用同余记号是完全等效的，称为不定方程表示。
如果我们在观念上将5**或5()当作为5的一个倍数，而不必知道是多少倍，当然也有一种意思是说，不必知道是正数倍还是负数倍；同时我们还要知道，这个项在等式两边移动与变号，并不影响等号两边的两个表达式的地位，认为两上表达式是处于对等的地位，而(±5**)可以在等式两边随意移动，对于两个表达式而言，他甚至成了第三方，有一些独立意味了。这样就与同余概念完全一致了。在同余概念下特称这个第三方为“模”，其实，它原本不过是一个乘法加法混合式（带余除法）中的一个因数（除数），只是我们不再强调他所连接的另一个因子，让他具有某种独立性了。
注2：
这里的k1称为乘率，或同余倒数，同余逆，模逆等等。见名知义，很容易理解。
注3：
利用不定方程来解，下面是我发现的一种综合了同余概念的本质，简化了不定方程的形式而得到的简化解法。
求解6*7k=1+5**
解：两边扣除5的倍数，归结到一起：
2k=1+5** 注意，我们不管5**是5的多少倍，只管将它们合并到一起，不必写成2k=1+5*(*-8k).
易见k可取值3.

对于难于计算的不定方程，用这样的思路同样容易解答。如果不便计算，将各次出现的**用具体的符号描述出来，将相邻的式子进行比较，比较所得的式子通常计算起来很方便。
由这些比较比，由后向前递推，比直接用原式来计算，方便得多。
而这种比较计算思路与不管中间过程中具体是多少倍的思路，及对同余式与不定方程之关系的特别的理解，是我个人的心得，一般数论书上没有讲述。愿朋友们理解之，并予阐发。

四：终结解答：
自然数x被5除余2,被6除余4,被7除余4,问这个数最小是多少
一：线性分解，必需的：
然后，假设将这个数分成三部分：x=x1+x2+x3
其中,
x1被5除余2,被6除余0,被7除余0,
x2被5除余0,被6除余4,被7除余0,
x3被5除余0,被6除余0,被7除余4,
二：转化
下面依此思路，另设
x=6*7a+5*7b+5*6c
代入原题或依上述x1,x2,x3之说明，得知：
6*7a=2 + 5**
5*7b=4+ 6**
5*6c=4+7**
易见可取a=1+5**， 特别地，取a=1
又 -b=4+6** (注：35b-6**得到-b), 故可取b=2 + 6**
又2c=4 + 7**, 故可取c= 2+ 7**
三：简化计算
易见x=5*6*7*(a/5+b/6+c/7),
=(a/5+b/6+c/7)以5*6*7为分母时的分子

剩下的，就是在分数
1/5+2/6+2/7如何计算他的分子上面做工夫了。
注意，这个分数为正的真分数，就对应于最小正整数解；为带分数，就对应于其他解。
因此，我们在中间计算时，对整体或每个小部分分数的值上加减一个整数，不影响我们最终的结果。并且，计算顺序，依加法交换律与分组结合律，如何方便如何计算。
结果是：172/210
验算：
自然数172是被5除余2,被6除余4,被7除余4的自然数中的最小值。

参考资料：http://zhidao.baidu.com/question/524218221

参考技术A 找出AB公倍数中除以C余1的最小的一个，乘以c
AC公倍数中除以B余1的最小的一个，乘以b
BC公倍数中除以C余1的最小的一个，乘以a
三个乘积相加减去ABC最小公倍数的整数倍追问

你不妨拿这个题举个例子呗 谢谢！

什么叫中国剩余定理

中国剩余定理释义：又称“孙子定理”。1852年，英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲。1874年，英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”。

孙子定理是中国古代求解一次同余式组（见同余）的方法。是数论中一个重要定理。又称中国余数定理。一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

扩展资料：

中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，方程组  有解，并且通解可以用如下方式构造得到：设 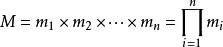 是整数m1,m2, ... ,mn的乘积，并设  是除了mi以外的n- 1个整数的乘积。

方程组  的通解形式为 

一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

宋朝数学家秦九韶于1247年《数书九章》卷一、二《大衍类》对“物不知数”问题做出了完整系统的解答。明朝数学家程大位将解法编成易于上口的《孙子歌诀》：

三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五使得知

这个歌诀给出了模数为3、5、7时候的同余方程的秦九韶解法。意思是：将除以3得到的余数乘以70，将除以5得到的余数乘以21，将除以7得到的余数乘以15，全部加起来后减去105（或者105的倍数），得到的余数就是答案。比如说在以上的物不知数问题里面，按歌诀求出的结果就是23。

参考资料：百度百科---孙子定理

参考技术A 如果正整数m1、m2、……、mk两两互质，那么同余方程组
x≡a,(mod mi), i=1,2,……k 有无穷多解。 且这些解关于模 M=m1,m2,……，mk同余，可表成
x≡a1,M'1M1+a2M'2M2+……+akM'KMK(mod M).
其中Mk=M/m,而M'k是满足M'kMk=1(mod mk)的正整数。这一算法后来传入西方，被称为中国剩余定理。

注：互质，也称互素。即两个数的最大公约数(最大公共因数，great common divisor)为1, 记号：gcd(a,b)=1.

名题：
三三数之剩二，置一百四十，五五数之剩三，置六十三，七七数之剩二，置三十，并之，得二百三十三，以二百一十减之，即得。凡三三数之剩一，则置七十，五五数之剩一，则置二十一，七七数之剩一，则置十五，即得。
即：
1、将军点兵，三三数余2，五五数余3，七七数余2。问兵几何？
2、今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?——《孙子算经》
由于孙子算经成书较早，并且较早地介绍了这样的问题，故中国剩余定理的众多异名中，一个著名的另名是：孙子定理。

写成数论记号：同余号≡以下简记为==
x==2 mod 3
==3 mod 5
==2 mod 7
这在数论中称为同余方程组，简称同余式组。

中国剩余定理就是求解同余式组的手段之一(注意，并不是唯一方法)。它的思想是这样的：
求出
x1==1 mod 3
==0 mod 5
==0 mod 7
x2==0 mod 3
==1 mod 5
==0 mod 7
x3==0 mod 3
==0 mod 5
==1 mod 7
那么2x1+3x2+2x3即为所求解x。

如果用向量记法，就更容易理解：
原题：x==(2,3,2) mod (3,5,7)
孙子定理：x1==(1,0,0);x2==(0,1,0);x3=(0,0,1)
x==2x1+3x2+2x3.

在求解x1时，显然x1==(0,0)mod (5,7),即x1被5，7整除。从而可设x1=5*7*k1==1 mod 3.
这里k1就是人们所说的乘率，古人求k1常用的就是大衍求一术。

这种方法实际上就是分化了维度，通过单位向量简化问题。近世代数的许多观点与方法，与这不谋而合，实际是受了中国剩余定理的启发。还有拉格朗日插值法，也与此一致。

同时我们还可以看到，x==(2,3,2) mod (3,5,7)
还可以等效于x==(2,2,2)+(0,1,0)，这样无疑是对上述算法的一种改进。正如牛顿插值法相对于拉格朗晶插值的改进。

以上内容，来自wsktuuytyh (用户名来源于姓名的五笔编码：wsk 何 tuu 冬 ytyh 州)的百度答题与博文。欢迎引用。欢迎交流。本回答被提问者和网友采纳 参考技术B

中国剩余定理（孙子定理）不足表现

中国剩余定理（孙子定理）不足表现