And Then There Was One（约瑟夫问题变形）

Posted 2020-06-16

题目链接：http://poj.org/problem?id=3517

And Then There Was One

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 5014		Accepted: 2685

Description

Let’s play a stone removing game.

Initially, n stones are arranged on a circle and numbered 1, …, n clockwise (Figure 1). You are also given two numbers k and m. From this state, remove stones one by one following the rules explained below, until only one remains. In step 1, remove stone m. In step 2, locate the k-th next stone clockwise from m and remove it. In subsequent steps, start from the slot of the stone removed in the last step, make k hops clockwise on the remaining stones and remove the one you reach. In other words, skip (k − 1) remaining stones clockwise and remove the next one. Repeat this until only one stone is left and answer its number. For example, the answer for the case n = 8, k = 5, m = 3 is 1, as shown in Figure 1.

Initial state	Step 1	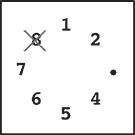Step 2	Step 3	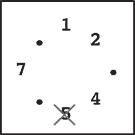Step 4
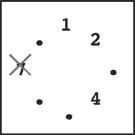Step 5	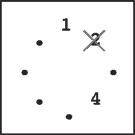Step 6	Step 7	Final state

Figure 1: An example game

Initial state: Eight stones are arranged on a circle.

Step 1: Stone 3 is removed since m = 3.

Step 2: You start from the slot that was occupied by stone 3. You skip four stones 4, 5, 6 and 7 (since k = 5), and remove the next one, which is 8.

Step 3: You skip stones 1, 2, 4 and 5, and thus remove 6. Note that you only count stones that are still on the circle and ignore those already removed. Stone 3 is ignored in this case.

Steps 4–7: You continue until only one stone is left. Notice that in later steps when only a few stones remain, the same stone may be skipped multiple times. For example, stones 1 and 4 are skipped twice in step 7.

Final State: Finally, only one stone, 1, is on the circle. This is the final state, so the answer is 1.

Input

The input consists of multiple datasets each of which is formatted as follows.

n k m

The last dataset is followed by a line containing three zeros. Numbers in a line are separated by a single space. A dataset satisfies the following conditions.

2 ≤ n ≤ 10000, 1 ≤ k ≤ 10000, 1 ≤ m ≤ n

The number of datasets is less than 100.

Output

For each dataset, output a line containing the stone number left in the final state. No extra characters such as spaces should appear in the output.

Sample Input

8 5 3
100 9999 98
10000 10000 10000
0 0 0

Sample Output

1
93
2019

题意：n个数排成一个圈，第一次删除m以后每次数到k个数删除一次，求最后一个被杉树的数
题解：是约瑟夫环问题的变形，距离上次学习约瑟夫环有一定时间了，上次不理解，这次理解递推的数学过程了:
当第n次，第f(n)个人出局了的时候剩下的n-1个人就构成了一个新的约瑟夫环问题，那么现在如果知道了第n-1次是第f(n-1)个人出局了，那么反着想，但是转化的时候是要从k+1个人开始计数，那么相当是吧k+1-->0;
k+2-->1.......所以在要想知道了f(n-1)想求f(n)就要用f(n) =  [k+1+f(n-1)]%n;现在好了递归函数出来了那么就可以写一个普通约瑟夫环的代码：

 1 #include<cstdio>
 2 using namespace std;
 3 int main()
 4 {
 5       int n,m,i,s = 0;
 6      printf("N M =");//n个数，每次数m个数出列
 7       scanf("%d%d",&n,&m);
 8      for(i = 2; i <= n; i++)
 9       {
10          s = (s + m) % i;
11       }
12       printf("\n The winner is %d\n",s+1);
13 }

 

这个题，要注意是从m开始计数的，但是由于递归的时候每次操作都是f(n) = (f(n-1)+k)%n;

但是实际上第一次的时候是删除掉了第m个数，而且编号是从1开始编号的，所以正常的将最后一组重新编号的时候f`(n) = [f(n-1)+m+1]%n; 所以最后答案应该是f`(n) = (m-k+1+f(n))%n;

ac代码：

 

 1 #include<cstdio>
 2 using namespace std;
 3 const int maxn = 10002;
 4 int f[maxn];
 5 
 6 int main()
 7 {
 8     int n, k, m;
 9     while(~scanf("%d%d%d",&n,&k,&m)){
10         if(n==0) return 0;
11         f[1] = 0;
12         for(int i = 2; i <= n; i++)f[i] = (f[i-1]+k)%i;
13         int ans = (m-k+1+f[n])%n;
14         if(ans<=0) ans+=n;//必须注意边界情况因为最后出现了-k所以要考虑负数的情况
15         printf("%d\n",ans);
16     }
17     return 0;
18 }