第二章 概率图模型的基本原理
Posted tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第二章 概率图模型的基本原理相关的知识,希望对你有一定的参考价值。
分为有向概率图模型(Directed Probabilistic Graphical Model),无向概率图模型(Undirected Probabilistic Graphical Model),混合概率图模型(Mixed Probabilistic Graphical Model)。
有向概率图模型:隐马尔科夫模型,贝叶斯网络,,动态贝叶斯网络
无向概率图模型:马尔科夫随机场,条件随机场
混合概率图模型:链图
隐马尔科夫模型(Hidden Markov Model, HMM)
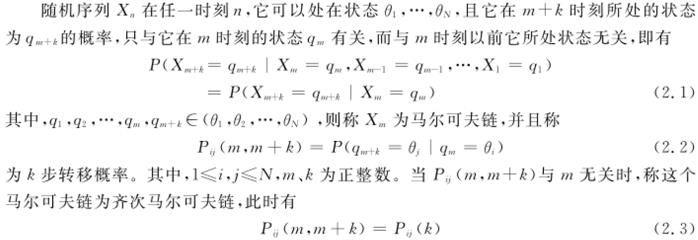

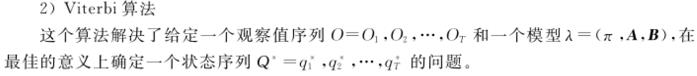

HMM算法实现的基本问题:
(1)初始模型选取
不同初始模型得到的结果不同
(2)多个观察值
可能有多个序列,然后对参数进行估计
(3)前向和后向算法以及Baum-Welch算法随着计算增加,计算结果的数值变小,可能产生下溢。
需要对
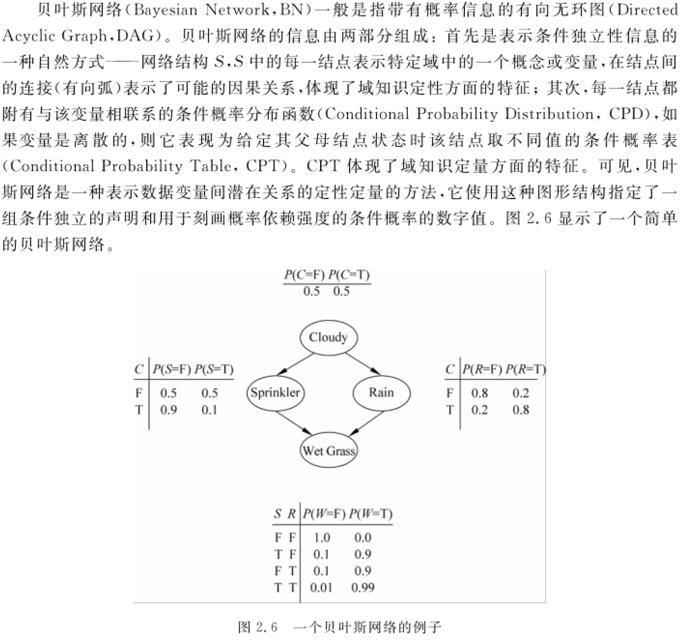
贝叶斯网络的学习包含两个主要过程:学习贝叶斯网络结构,学习参数。
几种常用的贝叶斯分类器:
(1)朴素贝叶斯网络(Naive Bayesian Networks, NBN):
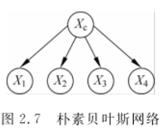
(2)通用贝叶斯网络(General Bayesian Networks, GBN)
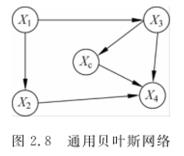

(3)增强型朴素贝叶斯网络(Tree-Augmented Naive Bayes, TAN)
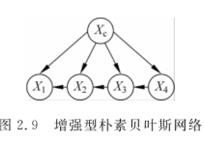


(4)马尔科夫毯贝叶斯网络(Markov Blanket Bayesian Networks, MBBN)
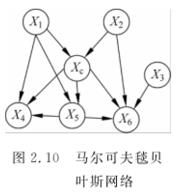

动态贝叶斯网络(Dynamic Bayesian Networks, DBNs)
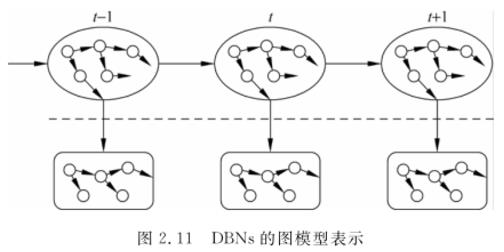


隐马尔科夫模型(HMM)和卡尔曼滤波模型(KFM)是两种典型的状态空间模型。
无向概率图模型(Undirected Probabilistic Graphical Model):
马尔科夫随机场(Markov Random Fields, MRFs):

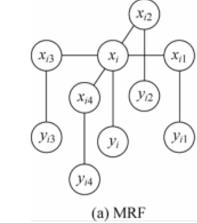
条件随机场(Conditional Random Fields, CRFs):

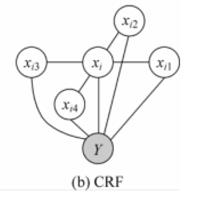
概率图模型的学习:分为结构学习和参数学习
结构学习:分为基于评分函数的学习(Scoring Function)和基于独立测试的学习(Conditional Independence Test, CIT)
评分函数:主要有基于贝叶斯统计的BDe(Bayesian Dirichlet-Likelihood Equivalent),最小描述长度MDL(Minimum Description Length),贝叶斯信息标准BIC(Bayesian Information Criterion)
基于独立测试的学习:常用的算法有CL算法,3阶段算法。
模型推理:分为精确推理与近似推理
精确推理:分为基于网络结构的推理与其他算法。
其他算法:包括图形简化法,证据扩散,汇聚算法,变量消元法,联合树算法。
近似推理:分为采样和搜索两种方法。
以上是关于第二章 概率图模型的基本原理的主要内容,如果未能解决你的问题,请参考以下文章