大话数据结构（十五）——二叉树的理论知识

Posted 2020-08-22 小企鹅ITgo

1 二叉树的存储结构

1.1 顺序存储结构

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，也是数组的下标要能体现结点之间的逻辑关系，比如双亲与孩子的关系。

一棵完全二叉树的存储：

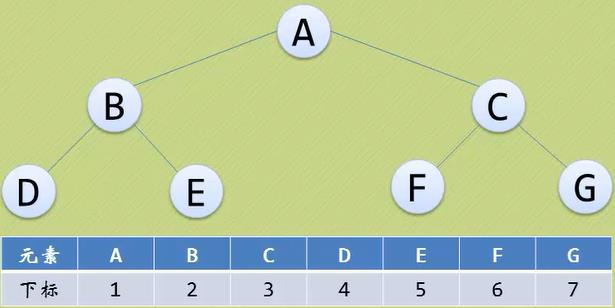
一般二叉树存储：尽管层序编号不能反映逻辑关系，但是可以将其按完全二叉树编号，只不过把不存在的结点设置为“^”。

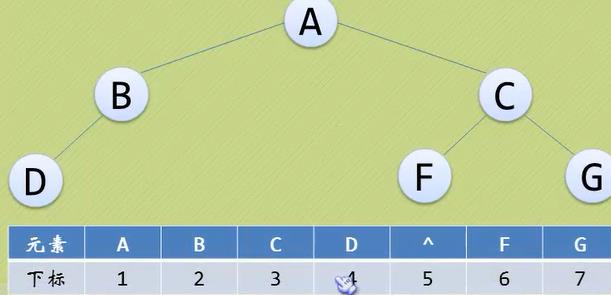
极端情况，右斜树，这不建议使用

 

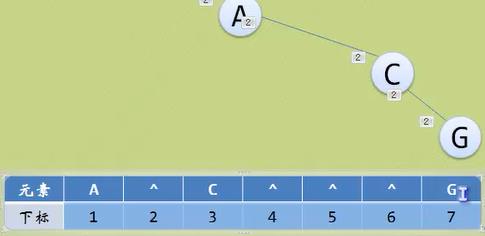
 1.2 二叉链表

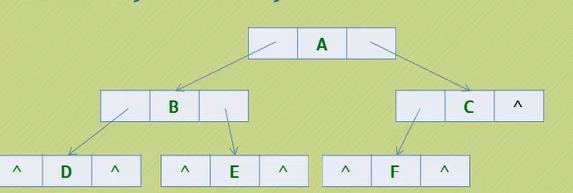
二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域是比较自然的，我们称这样的链表叫做二叉链表。

 

lchild

data

rchild

 

其中，data是数据域，lchild和rchild都是指针域，分别存放指向左孩子和右孩子的指针。

2 遍历二叉树

2.1 二叉树遍历原理

二叉树的遍历（traversing binary tree）是指从根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次。

2.2 二叉树遍历方法

2.2.1 前序遍历

规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

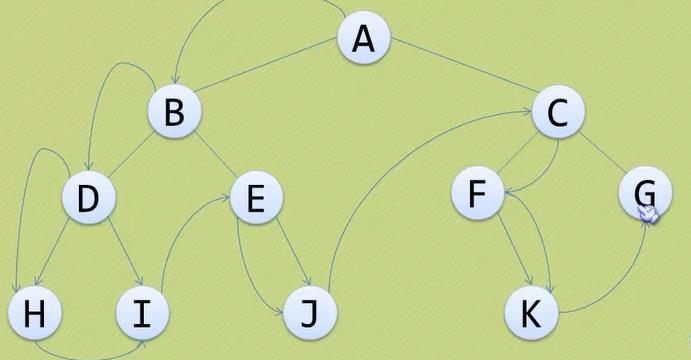
2.2.2 中序遍历

规则是若树为空，则空操作返回，否则从根结点开始（注意不是先访问根结点），中序遍历根节点的左子树，然后是访问根结点，最后中序遍历右子树。

 

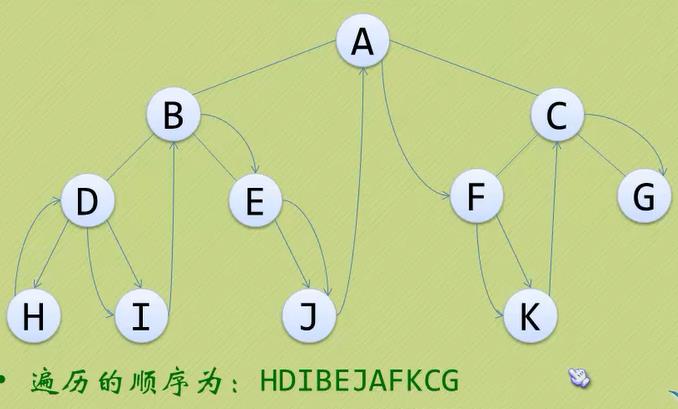
2.2.3 后序遍历

规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后访问根结点。

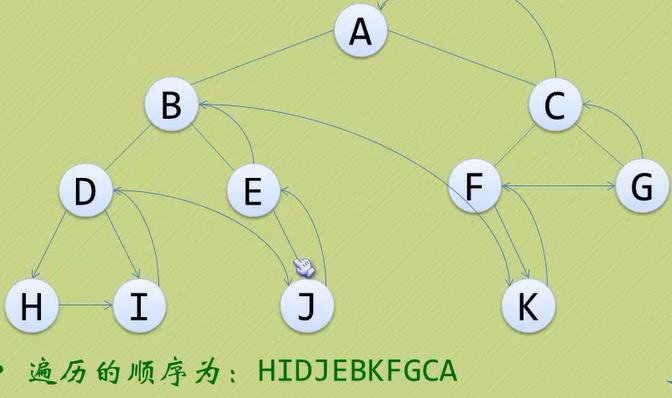
2.2.4 层序遍历

规则是若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。

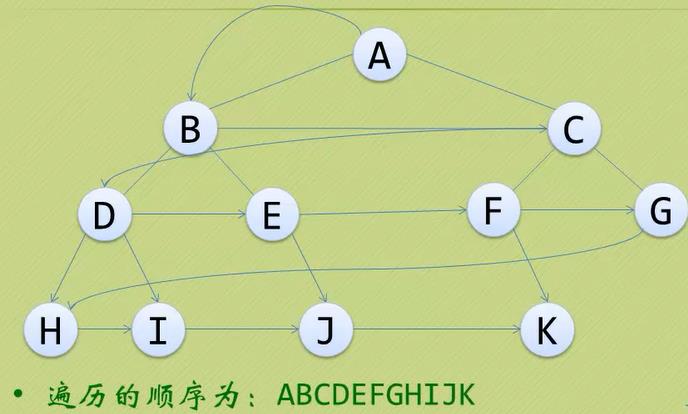
3、线索二叉树

之前的二叉树：

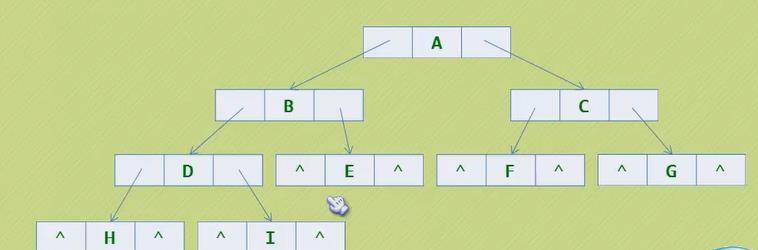
指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树（Treaded Binary Tree）。

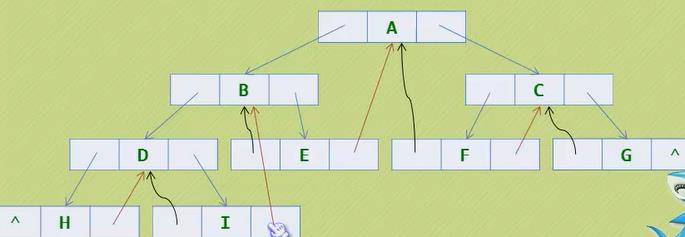
采用中序遍历：HDIBEAFCG

则黑线表示前驱，棕线表示后继。

 

对二叉树以某种次序遍历使其变为线索二叉树的过程就是线索化。

lchild

ltag

data

rtag

rchild

 

其中：

ltag为0时指向该结点的左孩子，为1时指向该结点的前驱；

rtag为0时指向该结点的右孩子，为1时指向该结点的后继。

4、树、森林与二叉树的转换

1、树转换为二叉树

1）加线。在所有兄弟结点之间一条连线

2）去线。对树中的每个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子结点之间的连线

3）层次调整。以树为根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。注意第一个孩子是二叉树的左孩子，兄弟转换过来的孩子是结点的右孩子。

2、森林转换为二叉树

1） 将每个树转为二叉树

2）第一棵二叉树不动，从第二棵树开始，依次把后一棵二叉树的根结点作为前一棵树的根结点的右孩子，用线连接。

3、二叉树转换为树

二叉树转为树是树转换二叉树的逆过程。

4、二叉树转换为森林

1）从根结点开始，若右孩子在，则把右孩子结点的连线删除，再查看分离后的二叉树，若右孩子在，则删除……直到把所有的右孩子连线都删除，得到二叉树

2）再将每棵树分离后的二叉树转换为树即可。