怎样用Matlab构建一个四维复数方阵?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了怎样用Matlab构建一个四维复数方阵?相关的知识,希望对你有一定的参考价值。
(1)构建一个4维复数方阵;
(2)求复数矩阵的相角;
(3)求复数矩阵的共轭复数矩阵;
(4)求复数矩阵的实部矩阵和虚部矩阵;
1、打开MATLAB软件,输入一下指令,清空工作空间和窗口界面;clear,clc。
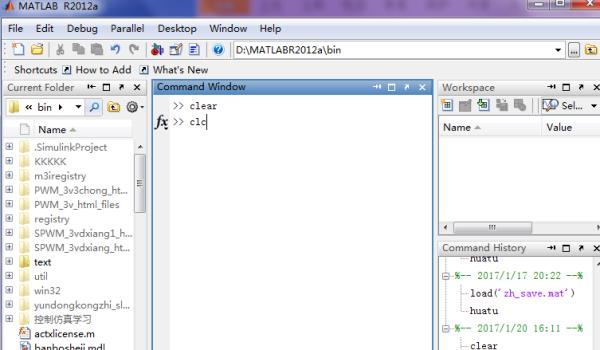
2、代数式复数生成:生成代码如下:a1=7+8*i。
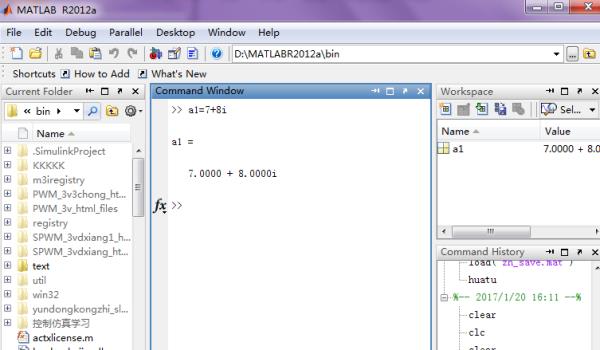
3、指数式复数生成:a2=5*exp(6*i)。
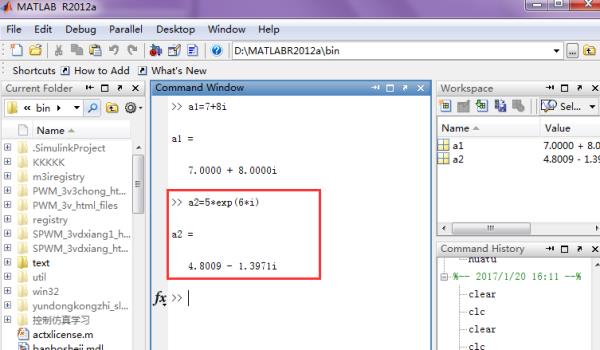
4、复数矩阵的生成:可以直接采用类似实矩阵的方法,a3=[2+2*i4-4*i5+6*i,3-5*i2-2*i4-8*i]。
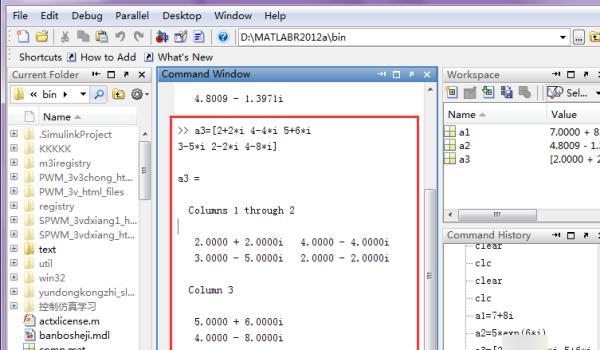
5、由实矩阵生成复矩阵:先生成两个实矩阵,分别对应复矩阵的实部与虚部,b1=randn(4,4);b2=rand(4,4);formatshort,a4=b1+b2*i。
参考技术A N = 10;Mat = rand(N, N, N, N) + rand(N, N, N, N)*1i;
a = angle(Mat);
b = conj(Mat);
r = real(Mat);
m = imag(Mat);追问
谢谢大神
本回答被提问者采纳用2个方阵模拟matlab的mrdivide
【中文标题】用2个方阵模拟matlab的mrdivide【英文标题】:Simulating matlab's mrdivide with 2 square matrices 【发布时间】:2015-09-22 15:08:12 【问题描述】:我有 2 个 19x19 方阵 (a & b),我正在尝试使用斜线 (mrdivide) 运算符来执行除法,这样
c = a / b
我正在尝试在 OpenCV 中实现这一点。我发现有一些人建议使用 cv::solve,但到目前为止,我一直找不到任何可以让我得到接近 matlab 的结果。
有谁知道我如何用 opencv 实现 mrdivide?p>
我试过以下代码:
cv::Mat mldivide(const cv::Mat& A, const cv::Mat& B )
//return b * A.inv();
cv::Mat a;
cv::Mat b;
A.convertTo( a, CV_64FC1 );
B.convertTo( b, CV_64FC1 );
cv::Mat ret;
cv::solve( a, b, ret, cv::DECOMP_NORMAL );
cv::Mat ret2;
ret.convertTo( ret2, A.type() );
return ret2;
然后我按如下方式实现了 mrdivide:
cv::Mat mrdivide(const cv::Mat& A, const cv::Mat& B )
return mldivide( A.t(), B.t() ).t();
(编辑:根据答案,当我正确使用它时,这确实给了我正确的答案!)
这给了我一个错误的答案,即不像matlab。根据 cmets 我也试过了
cv::Mat mrdivide(const cv::Mat& A, const cv::Mat& B )
return A * B.inv();
这给出了与上面相同的答案,但也是错误的。
【问题讨论】:
a/b = (b'\a')',所以尝试实现这个操作。 您也可以尝试反转b,然后乘以a。您是否考虑过查看cv::invert 函数? docs.opencv.org/modules/core/doc/… 。此外,目前在 OpenCV 中有三种反转矩阵的方法。这篇 *** 帖子介绍了相对较大矩阵大小的每个函数的时序:***.com/questions/11040333/…
@Goz - 这与mrdivide 不同。你需要做A * B.inv()。在MATLAB中做B.inv()*A和B\A是一样的,这不是你想要的,对吧?
@rayryeng:对不起,这实际上是我的意思。我正在尝试一些东西并粘贴了错误的代码。
@Goz - 啊,我明白了。嗯……你能给我们举个例子吗?距离有多远?
【参考方案1】:
您不应该使用inv 来解决Ax=b 或xA=b 方程。虽然这两种方法在数学上是等价的(x=solve(A,b) 和 x=inv(A)*B),但在处理浮点数时却完全不同!
http://www.johndcook.com/blog/2010/01/19/dont-invert-that-matrix/
作为一般规则,切勿乘以矩阵求逆。而是对一次性系统使用正/反斜杠运算符(或等效的“求解”方法),或者当您想重用相同的 @ 时显式执行矩阵分解(想想 LU、QR、Cholesky 等)。 987654347@与多个b的
让我举一个具体的例子来说明反转的问题。我将使用 MATLAB 和 mexopencv,这是一个允许我们直接从 MATLAB 调用 OpenCV 的库。
(这个例子是从 this excellent FEX submission 借来的,他是 SuiteSparse 背后的同一个人。我正在展示左除法 Ax=b 的情况,但同样适用于右除法 xA=b )。
让我们首先为Ax=b系统构建一些矩阵:
% Ax = b
N = 16; % square matrix dimensions
x0 = ones(N,1); % true solution
A = gallery('frank',N); % matrix with ill-conditioned eigenvalues
b = A*x0; % Ax=b system
这是 16x16 矩阵 A 和 16x1 向量 b 的样子(请注意,真正的解 x0 只是一个 1 的向量):
A = b =
16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 136
15 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 135
0 14 14 13 12 11 10 9 8 7 6 5 4 3 2 1 119
0 0 13 13 12 11 10 9 8 7 6 5 4 3 2 1 104
0 0 0 12 12 11 10 9 8 7 6 5 4 3 2 1 90
0 0 0 0 11 11 10 9 8 7 6 5 4 3 2 1 77
0 0 0 0 0 10 10 9 8 7 6 5 4 3 2 1 65
0 0 0 0 0 0 9 9 8 7 6 5 4 3 2 1 54
0 0 0 0 0 0 0 8 8 7 6 5 4 3 2 1 44
0 0 0 0 0 0 0 0 7 7 6 5 4 3 2 1 35
0 0 0 0 0 0 0 0 0 6 6 5 4 3 2 1 27
0 0 0 0 0 0 0 0 0 0 5 5 4 3 2 1 20
0 0 0 0 0 0 0 0 0 0 0 4 4 3 2 1 14
0 0 0 0 0 0 0 0 0 0 0 0 3 3 2 1 9
0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2
现在让我们比较cv::invert 和cv::solve,通过使用NORM 函数(或cv::norm,如果需要)找到解决方案并计算残差:
% inverting (OpenCV)
x1 = cv.invert(A)*b;
r1 = norm(A*x1-b)
% inverting (MATLAB)
x2 = inv(A)*b;
r2 = norm(A*x2-b)
% solve using matrix factorization (OpenCV)
x3 = cv.solve(A,b);
r3 = norm(A*x3-b)
% solve using matrix factorization (MATLAB)
x4 = A\b;
r4 = norm(A*x4-b)
以下是找到的解决方案(我减去1,这样您就可以看到它们与真正的解决方案x0 相差多远):
>> format short g
>> [x1 x2 x3 x4] - 1
ans =
9.0258e-06 3.1086e-15 -1.1102e-16 2.2204e-16
-0.0011101 -1.0181e-13 -2.2204e-15 -2.3315e-15
-0.0016212 -2.5123e-12 3.3751e-14 3.3307e-14
0.0037279 4.1745e-11 -4.3476e-13 -4.3487e-13
-0.0022119 4.6216e-10 5.2165e-12 5.216e-12
-0.0010476 1.3224e-09 -5.7384e-11 -5.7384e-11
0.0035461 2.2614e-08 5.7384e-10 5.7384e-10
-0.0040074 -4.1533e-07 -5.1646e-09 -5.1645e-09
0.0036477 -4.772e-06 4.1316e-08 4.1316e-08
-0.0033358 4.7499e-06 -2.8922e-07 -2.8921e-07
0.0059112 -0.00010352 1.7353e-06 1.7353e-06
-0.0043586 0.00044539 -8.6765e-06 -8.6764e-06
0.0069238 -0.0024718 3.4706e-05 3.4706e-05
-0.0019642 -0.0079952 -0.00010412 -0.00010412
0.0039284 0.01599 0.00020824 0.00020823
-0.0039284 -0.01599 -0.00020824 -0.00020823
最重要的是,以下是每种方法的错误:
r1 =
0.1064
r2 =
0.060614
r3 =
1.4321e-14
r4 =
1.7764e-15
最后两个更准确的数量级,甚至没有接近!这只是一个由 16 个变量组成的系统。求逆在数值上不太可靠,尤其是当矩阵又大又稀疏时...
现在回答您的问题,您使用cv::solve 的想法是正确的,但是在右除的情况下您只是弄错了操作数的顺序。
在 MATLAB 中,运算符 / 和 \(或 mrdivide 和 mldivide)通过等式 B/A = (A'\B')' 相互关联(这是 transpose properties 的简单结果)。
所以对于 OpenCV 函数,你会写(注意 A 和 b 的顺序):
% Ax = b
x = cv.solve(A, b); % A\b or mldivide(A,b)
% xA = b
x = cv.solve(A', b')'; % b/A or mrdivide(b,A)
OpenCV 暴露的 API 在这里有点笨拙,所以我们不得不做所有这些转置。事实上,如果您参考equivalent LAPACK 例程(想想DGESV 或DGESVX),它们实际上允许您指定矩阵是否转置TRANS=T 或不TRANS=N(在那个级别,转置实际上只是不同的内存布局,C 或 Fortran 排序)。例如,MATLAB 提供了linsolve 函数,它允许您在选项中指定这些类型的东西...
(顺便说一句,在 C++ OpenCV 中编码时,我更喜欢使用像 cv::transpose 这样的函数形式的运算,而不是像 Mat::t 这样的矩阵表达式变体。前者可以就地操作,而后者会创建不必要的临时副本)。
现在,如果您正在寻找 C++ 中性能良好的线性代数实现,请考虑使用 Eigen(甚至是 integrate nicely with OpenCV)。此外,它是一个纯粹的基于模板的库,因此无需担心链接或二进制文件,只需包含头文件即可。
编辑(响应 cmets)
@Goz:
查找返回值优化。 “不必要的临时副本”不存在
我知道RVO 和move semantics,但这在这里并不重要;无论如何,cv::Mat 类是copy-friendly,有点像引用计数的智能指针。这意味着它只在按值传递时进行数据共享的浅拷贝。为新副本创建的唯一部分是 mat header 中的部分,这些部分在大小方面无关紧要(存储诸如维度/通道数、步长和数据类型之类的东西)。
我说的是一个显式的深拷贝,而不是你从函数调用返回时考虑的那个......
感谢您的评论,这让我有动力去实际挖掘 OpenCV 源代码,这不是最容易阅读的东西……代码几乎没有 cmets,有时很难理解。看到 OpenCV 真正关心性能,其复杂性是可以理解的,实际上令人印象深刻的是,许多功能以各种方式实现(常规 CPU 实现、循环展开版本、SIMD 矢量化版本(SSE、AVX、NEON 等)、并行和线程化使用各种后端的版本、来自 Intel IPP 的优化实现、带有 OpenCL 或 CUDA 的 GPU 加速版本、用于 Tegra、OpenVX 等的移动加速版本)
让我们以下面的案例来追踪我们的步骤:
Mat A = ..., b = ..., x;
cv::solve(A.t(), b, x);
函数的定义如下:
bool cv::solve(InputArray _src, InputArray _src2arg, OutputArray _dst, int method)
Mat src = _src.getMat(), _src2 = _src2arg.getMat();
_dst.create( src.cols, _src2.cols, src.type() );
Mat dst = _dst.getMat();
...
现在我们必须弄清楚中间的步骤。我们拥有的第一件事是t 成员方法:
MatExpr Mat::t() const
MatExpr e;
MatOp_T::makeExpr(e, *this);
return e;
这会返回一个MatExpr,它是一个允许对matrix expressions 进行惰性求值的类。换句话说,它不会立即执行转置,而是存储对原始矩阵的引用以及最终对其执行的操作(转置),但它会推迟评估它,直到绝对必要(例如当分配或转换为 cv::Mat)。
接下来我们看看相关部分的定义。请注意,在实际代码中,这些内容被拆分到许多文件中。为了方便阅读,我只拼凑了有趣的部分,但远非完整:
class MatExpr
public:
MatExpr()
: op(0), flags(0), a(Mat()), b(Mat()), c(Mat()), alpha(0), beta(0), s()
explicit MatExpr(const Mat& m)
: op(&g_MatOp_Identity), flags(0), a(m), b(Mat()), c(Mat()),
alpha(1), beta(0), s(Scalar())
MatExpr(const MatOp* _op, int _flags, const Mat& _a = Mat(),
const Mat& _b = Mat(), const Mat& _c = Mat(),
double _alpha = 1, double _beta = 1, const Scalar& _s = Scalar())
: op(_op), flags(_flags), a(_a), b(_b), c(_c), alpha(_alpha), beta(_beta), s(_s)
MatExpr t() const
MatExpr e;
op->transpose(*this, e);
return e;
MatExpr inv(int method) const
MatExpr e;
op->invert(*this, method, e);
return e;
operator Mat() const
Mat m;
op->assign(*this, m);
return m;
public:
const MatOp* op;
int flags;
Mat a, b, c;
double alpha, beta;
Scalar s;
Mat& Mat::operator = (const MatExpr& e)
e.op->assign(e, *this);
return *this;
MatExpr operator * (const MatExpr& e1, const MatExpr& e2)
MatExpr en;
e1.op->matmul(e1, e2, en);
return en;
到目前为止,这很简单。该类应该将输入矩阵存储在a 中(同样cv::Mat 实例将共享数据,因此不能复制),以及执行op 的操作,以及其他一些对我们不重要的事情。
这是矩阵运算类MatOp,以及它的一些子类(我只展示了转置和逆运算,但还有更多):
class MatOp
public:
MatOp();
virtual ~MatOp();
virtual void assign(const MatExpr& expr, Mat& m, int type=-1) const = 0;
virtual void transpose(const MatExpr& expr, MatExpr& res) const
Mat m;
expr.op->assign(expr, m);
MatOp_T::makeExpr(res, m, 1);
virtual void invert(const MatExpr& expr, int method, MatExpr& res) const
Mat m;
expr.op->assign(expr, m);
MatOp_Invert::makeExpr(res, method, m);
class MatOp_T : public MatOp
public:
MatOp_T()
virtual ~MatOp_T()
void assign(const MatExpr& expr, Mat& m, int type=-1) const
Mat temp, &dst = _type == -1 || _type == e.a.type() ? m : temp;
cv::transpose(e.a, dst);
if( dst.data != m.data || e.alpha != 1 ) dst.convertTo(m, _type, e.alpha);
void transpose(const MatExpr& e, MatExpr& res) const
if( e.alpha == 1 )
MatOp_Identity::makeExpr(res, e.a);
else
MatOp_AddEx::makeExpr(res, e.a, Mat(), e.alpha, 0);
static void makeExpr(MatExpr& res, const Mat& a, double alpha=1)
res = MatExpr(&g_MatOp_T, 0, a, Mat(), Mat(), alpha, 0);
;
class MatOp_Invert : public MatOp
public:
MatOp_Invert()
virtual ~MatOp_Invert()
void assign(const MatExpr& e, Mat& m, int _type=-1) const
Mat temp, &dst = _type == -1 || _type == e.a.type() ? m : temp;
cv::invert(e.a, dst, e.flags);
if( dst.data != m.data ) dst.convertTo(m, _type);
void matmul(const MatExpr& e1, const MatExpr& e2, MatExpr& res) const
if( isInv(e1) && isIdentity(e2) )
MatOp_Solve::makeExpr(res, e1.flags, e1.a, e2.a);
else if( this == e2.op )
MatOp::matmul(e1, e2, res);
else
e2.op->matmul(e1, e2, res);
static void makeExpr(MatExpr& res, int method, const Mat& m)
res = MatExpr(&g_MatOp_Invert, method, m, Mat(), Mat(), 1, 0);
;
static MatOp_Identity g_MatOp_Identity;
static MatOp_T g_MatOp_T;
static MatOp_Invert g_MatOp_Invert;
OpenCV 大量使用运算符重载,因此A+B、A-B、A*B 等各种运算实际上映射到相应的矩阵表达式运算。
谜题的最后一部分是代理类InputArray。它基本上存储了一个void* 指针以及有关传递的东西的信息(它是什么类型:Mat、MatExpr、Matx、vector<T>、UMat 等),这样它就知道了如何在使用 InputArray::getMat 之类的请求时将指针转换回:
typedef const _InputArray& InputArray;
class _InputArray
public:
_InputArray(const MatExpr& expr)
init(FIXED_TYPE + FIXED_SIZE + EXPR + ACCESS_READ, &expr);
void init(int _flags, const void* _obj)
flags = _flags; obj = (void*)_obj;
Mat getMat_(int i) const
int k = kind();
int accessFlags = flags & ACCESS_MASK;
...
if( k == EXPR )
CV_Assert( i < 0 );
return (Mat)*((const MatExpr*)obj);
...
return Mat();
protected:
int flags;
void* obj;
Size sz;
现在我们看到Mat::t 如何创建并返回MatExpr 实例。然后由cv::solve 作为InputArray 接收。现在,当它调用InputArray::getMat 来检索矩阵时,它有效地将存储的MatExpr 转换为调用强制转换运算符的Mat:
MatExpr::operator Mat() const
Mat m;
op->assign(*this, m);
return m;
因此它声明了一个新矩阵m,调用MatOp_T::assign,并将新矩阵作为目标。反过来,这迫使它通过最终调用cv::transpose 进行评估。它将转置结果计算到这个新矩阵中作为目标。
所以我们最终得到了两个副本,原始的A 和转置的A.t() 返回。
现在说了这么多,对比一下:
Mat A = ..., b = ..., x;
cv::transpose(A, A);
cv::solve(A, b, x);
在这种情况下,A 被转置就地,并且抽象级别较低。
现在我展示所有这些的原因不是为了争论这个额外的副本,毕竟这没什么大不了的 :) 我发现的真正巧妙的事情是,以下两个表达式没有做同样的事情并给出不同的结果(而且我不是在谈论逆是否就位):
Mat A = ..., b = ..., x;
cv::invert(A,A);
x = A*b;
Mat A = ..., b = ..., x;
x = inv(A)*b;
事实证明,第二个实际上足够聪明,可以打电话给cv::solve(A,b)!如果你回到MatOp_Invert::matmul(当惰性求逆稍后与另一个惰性矩阵乘法链接时调用)。
void MatOp_Invert::matmul(const MatExpr& e1, const MatExpr& e2, MatExpr& res) const
if( isInv(e1) && isIdentity(e2) )
MatOp_Solve::makeExpr(res, e1.flags, e1.a, e2.a);
...
它检查表达式inv(A)*B 中的第一个操作数是否为求逆运算,第二个操作数是否为单位运算(即普通矩阵,而不是另一个复杂表达式的结果)。在这种情况下,它将存储的操作更改为惰性求解操作MatOp_Solve(它同样是cv::solve 函数的包装器)。 IMO 这很聪明!即使您写了inv(A)*b,它实际上也不会计算逆,相反,它知道最好通过使用矩阵分解求解系统来重写它。
不幸的是,这只会使inv(A)*b 形式的表达式受益,而不是b*inv(A) 的相反方式(最终会计算出我们不想要的逆)。所以在你解决xA=b的情况下,你应该坚持显式调用cv::solve...
当然,这仅适用于使用 C++ 编码时(感谢运算符重载和惰性表达式的魔力)。如果您使用某些包装器(如 Python、Java、MATLAB)从另一种语言中使用 OpenCV,您可能不会得到任何这些,并且应该像我在之前的 MATLAB 代码中所做的那样明确使用 cv::solve,因为Ax=b 和 xA=b 两种情况。
希望这会有所帮助,对于长篇文章感到抱歉;)
【讨论】:
这应该是公认的答案。干得好阿姆罗。这很有趣,因为我记得约翰库克的那篇文章......我什至推荐人们阅读它......但我违背了我更好的判断并想快速尝试一些东西。令我困惑的是 OP 如何无法使其工作。 btw .. 查找返回值优化。 “不必要的临时副本”不存在,它使我更容易理解代码。它还允许 const 正确性,这可以提供比使用 C 样式接口更好的编译器优化。 @Amro: 哇......如果可以的话,我会给你第二次投票......在这个线程中帮助我解决我的 mldivide 问题:***.com/questions/32741319/… ? :D【参考方案2】:在 MATLAB 中,在两个具有兼容维度的矩阵上使用 mrdivide,使得 a / b 等价于 a * b^-1,其中 b^-1 是 b 的倒数。因此,您可以做的可能是先反转矩阵b,然后预乘这个a。
一种方法是在矩阵b 上使用cv::invert,然后与a 预乘。这可以通过以下函数定义来完成(借鉴您上面帖子中的代码):
cv::Mat mrdivide(const cv::Mat& A, const cv::Mat& B)
cv::Mat bInvert;
cv::invert(B, bInvert);
return A * bInvert;
另一种方法是使用cv::Mat 接口内置的inv() 方法,然后使用该方法并将矩阵本身相乘:
cv::Mat mrdivide(const cv::Mat& A, const cv::Mat& B)
return A * B.inv();
我不确定哪一种更快,因此您可能需要进行一些测试,但这两种方法中的任何一种都应该有效。然而,为了提供一些可能的时序方面的见解,在 OpenCV 中有三种方法可以反转矩阵。您只需将第三个参数覆盖为cv::invert 或指定cv::Mat.inv() 中的方法即可。
这篇 *** 帖子介绍了使用三种方法为相对较大的矩阵大小反转矩阵的时间:Fastest method in inverse of matrix
【讨论】:
no Ray,不要使用inv 来求解线性系统!它既慢又不准确。您应该改用具有适当矩阵分解的求解方法..
@Amro - 你肯定是对的。不过我能想到的最快的事情。以上是关于怎样用Matlab构建一个四维复数方阵?的主要内容,如果未能解决你的问题,请参考以下文章
我现在有一个300*41*768的四维数据,但是MATLAB不能显示四维数据,如何减维数,画出三维图形的效果?