算法：快速排序

Posted 2020-08-22 子烁爱学习

算法：快速排序

快速排序

　　其实我第一次听到快速排序的时候，我就很纳闷，因为不像冒泡、插入、归并、选择排序等等，名称即原理！这个直接把特性用作名称的，我就很震惊！

　　咱还是直接瞅一眼百科的解释吧！

　　快速排序是冒泡排序的改进。

　　快速排序由C. A. R. Hoare在1960年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

　　百科中解释了快排的一趟操作是对无序数组进行分割，使其分为左右两半部分，左边的都小于某个数，右边的都大于每个数。那某个数是哪个数呢？这个就是无所谓的，随便取一个数就好，要不就以第1个数作为那个数吧！

　　

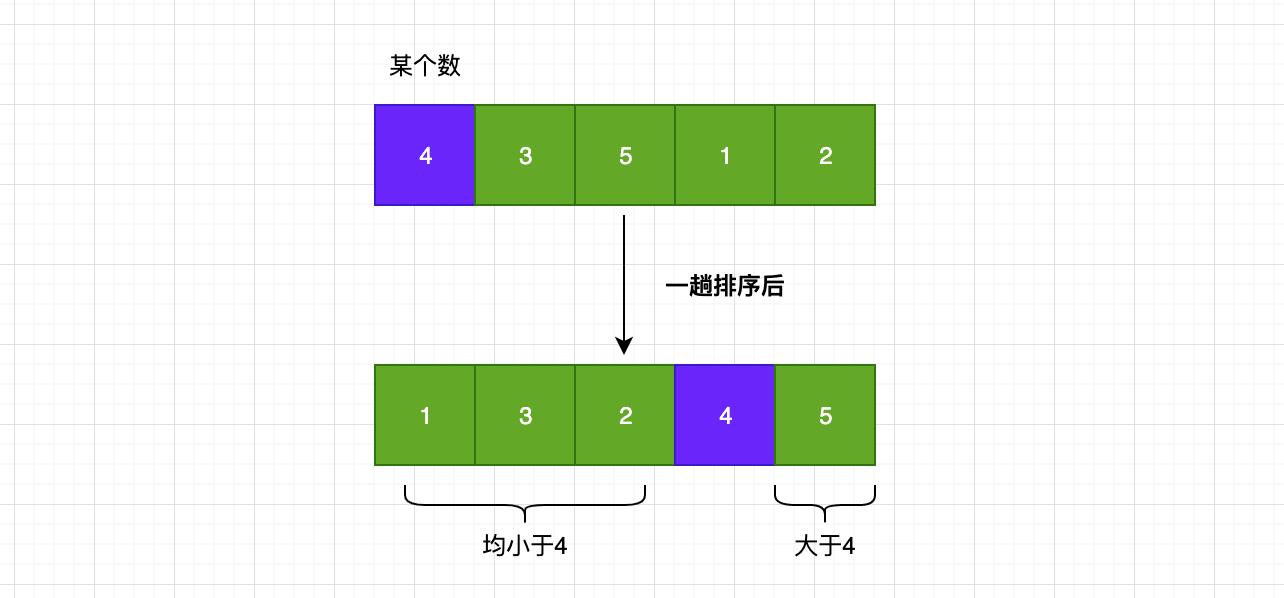
　　就像上图这样，一趟排序使得小于4的处于左边，大于4的处于右边！

一趟排序

 　　那一趟排序到底做了什么呢？它具体是怎么使得元素位置进行如图变换的呢！

　　其实也很简单，我们之前有讲过双指针的应用，我们两边分别定义指针i，j。i从左到右走，负责找大于4的，j从右往左走，负责找小于4的。

　　

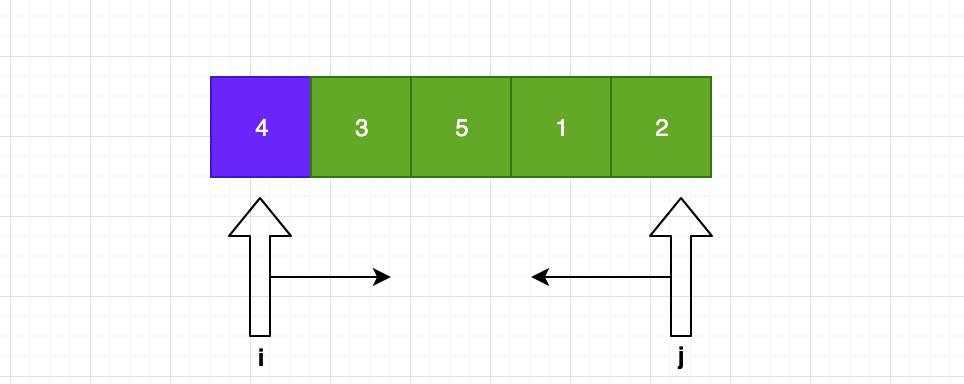
　　到找到之后，他俩所在位置的元素一交换，就使得大的值处于右边，小的值处于左边！

　　

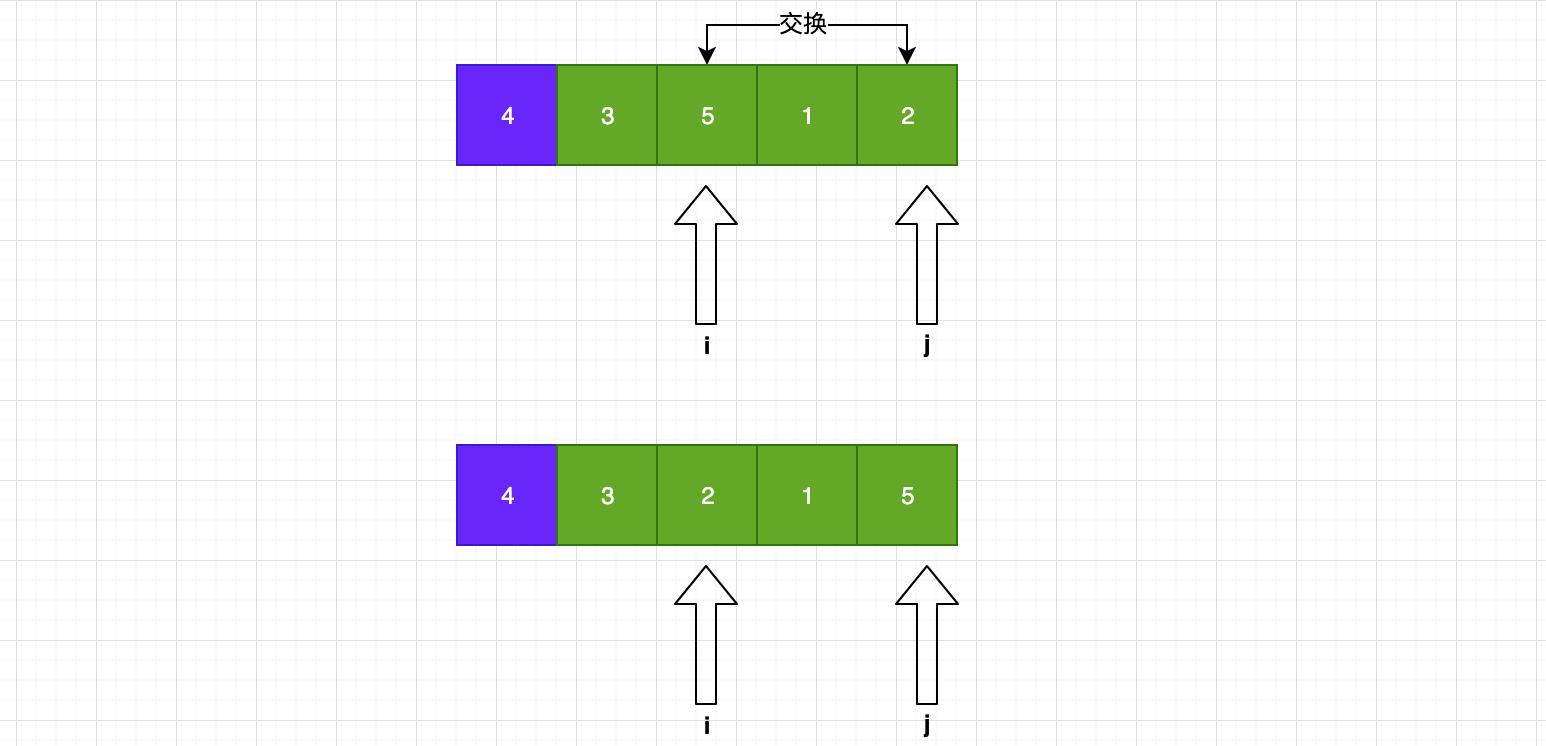
　　接着呢，i和j继续移动，直到他俩相遇！此时我们将当前位置与1号位置交换，就把4放在中间了！讲是这么讲，但是这个过程还是有很多需要注意的地方！！！

　　

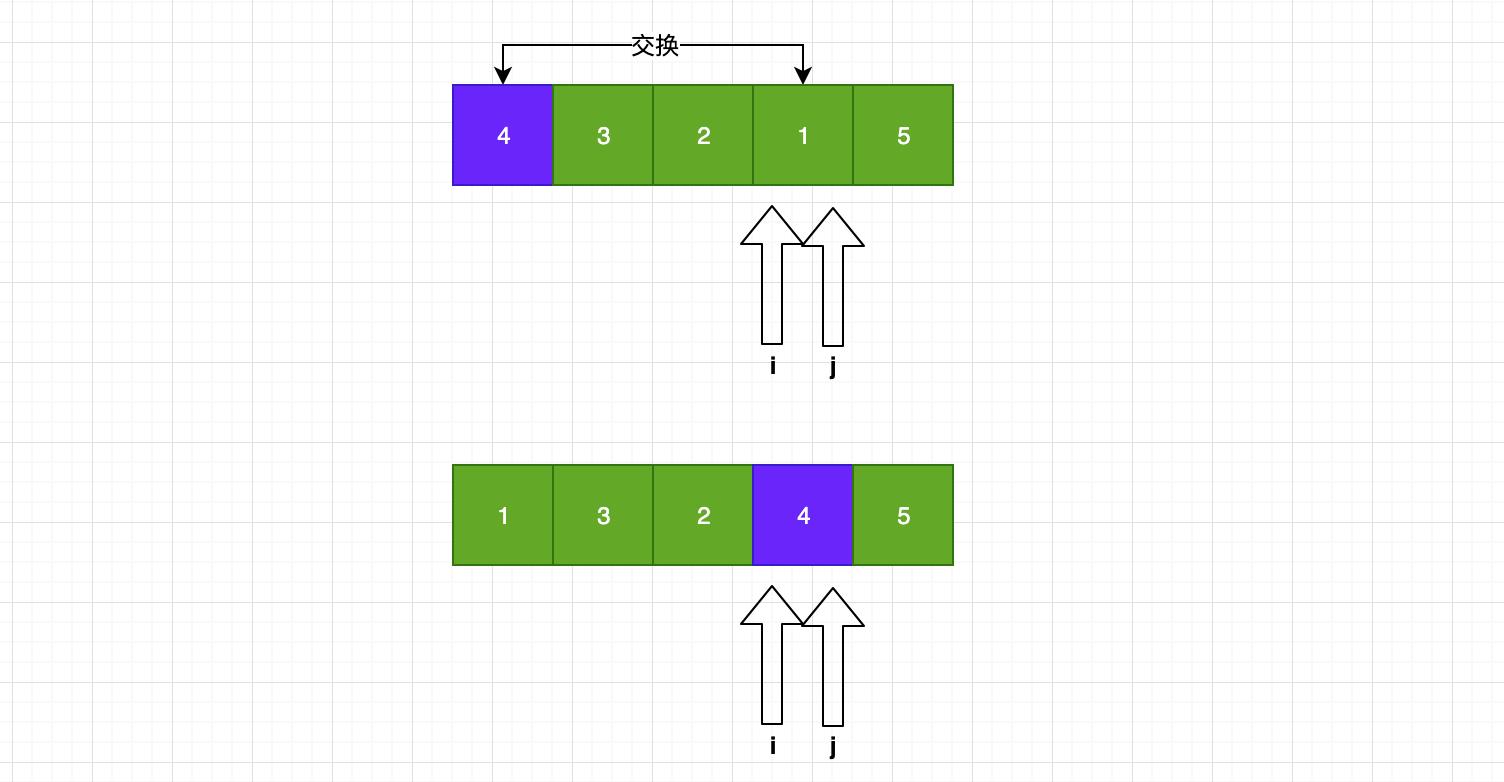
接着

　　一趟排序完之后呢?其实我们只是把一个元素的最终位置确定了，即4！也是就说4肯定是在这里放，那我们还需要处理其他的，所以仍然需要对4左边的一趟排序，对4的右边的一趟排序！那当然直观的看，4右边就一个元素5所以肯定是有序的！

　　那左边132，经过一趟排序后！其实1的位置还是没有变，1左边没有了，我们需要对1右边的元素进行一趟排序！

　　

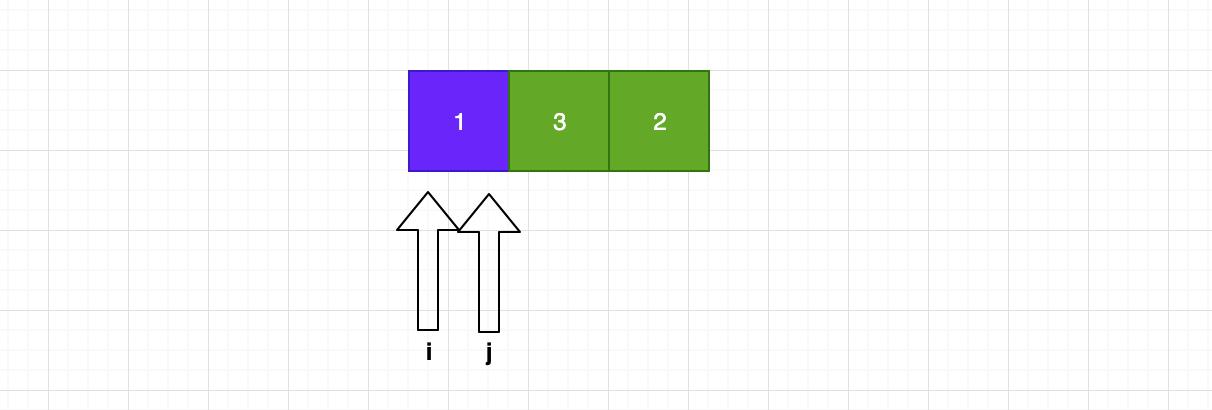
　　好了，对右边进行一趟排序后，结果如下：

　　

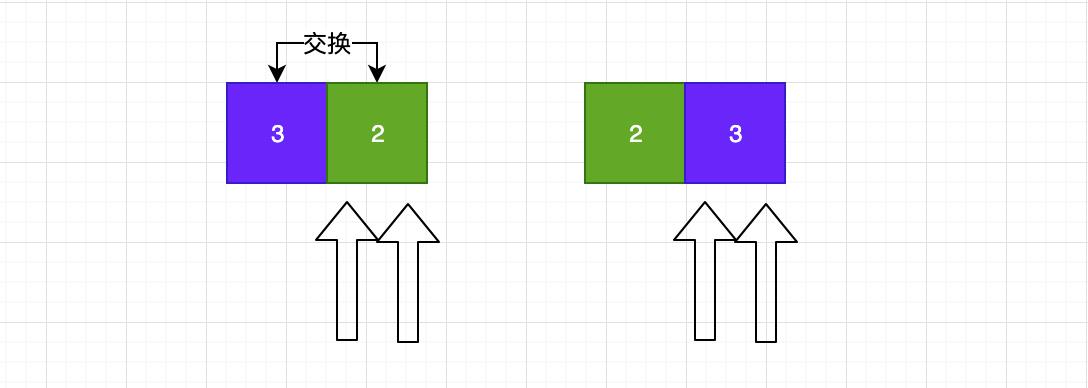
　　因为我们是分别处理的，所以我们画的都是部分图，最终效果就是整体有序！

　　这个就是快速排序的核心思想了，我们可以简单总结一下，我们将序列根据某个值分为两段，这个成为一趟排序，此时该值的最终位置就确定了，接着再对两段进行一趟排序，来确定两侧元素的的最终位置。每一段都要进行一趟操作，所以着很明显是递归操作！我们在代码中可以很明显的看到！

分析一下

　　快速排序的一次划分算法从两头交替搜索，直到i和j重合，因此其时间复杂度是O(n)；而整个快速排序算法的时间复杂度与划分的趟数有关!

　　理想的情况是，每次划分所选择的中间数恰好将当前序列几乎等分，经过log2n趟划分，便可得到长度为1的子表。这样，整个算法的时间复杂度为O(nlog2n)。

　　最坏的情况是，每次所选的中间数是当前序列中的最大或最小元素，这使得每次划分所得的子表中一个为空表，另一子表的长度为原表的长度-1。这样，长度为n的数据表的快速排序需要经过n趟划分，使得整个排序算法的时间复杂度为O(n^2)。

　　当然快排也不稳定！！位于后面的元素很有可能会拍到前面，这个发生在一趟排序过程中，仔细想想！

Java实现

　　理解思路后，再看代码其实还是蛮简单的！ 

package sort;

import java.util.Arrays;

/**
 * 快速排序
 * @author mrsaber
 */
public class QuickSort {

    public static void main(String[] args) {
        int[] arr = new int[]{4,3,2,1,5,6,7,8,3,1,3,111,22,9};
        new QuickSort().sort(arr,0,arr.length-1);
        System.out.println(Arrays.toString(arr));
    }

    public void sort(int[] nums,int start,int end){
        if(end-start<1)
            return;
        int i = start;
        int j = end;
        while (j>i){
            while (j>=0&&j>i&&nums[j]>nums[start]){j--;}
            while (i<end&&i<j&&nums[i]<=nums[start]){i++;}
            if(i<j){
                swap(nums,i,j);
            }
        }
        swap(nums,i,start);
        sort(nums,start,i-1);
        sort(nums,i+1,end);
    }



    /**
     * 数组元素交换
     * @param nums
     * @param i
     * @param j
     */
    public void swap(int[] nums,int i,int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] =temp;
    }
}

参考资料

• 《百度百科》