算法导论归并排序

Posted 2020-08-22

递归与分治

   许多有用的算法在结构上是递归的：为了解决一个给定的问题，算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。这些算法典型地遵循分治法的思想：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

   分治模式在每层递归时都有三个步骤：

1. 分解原问题为若干子问题，这些子问题是原问题的规模较小的实例。
2. 解决这些子问题，递归地求解各子问题。然而，若子问题的规模足够小，则直接求解。
3. 合并这些子问题的解成原问题的解。

归并排序

   归并排序算法完全遵循分治模式。直观上其操作如下：

   （1）分解：分解等排序的n个元素的序列成各具n/2个元素的两个子序列；

   （2）解决：使用归并排序递归地排序两个子序列；

   （3）合并：合并两个已排序的子序列以产生已排序的答案。

   当待排序的序列长度为1时，递归"开始回升"，在这种情况下不根做任何工作，因为长度为1的每个序列都已排好序。

   归并排序算法的关键操作是"合并"步骤中两个已排序序列的合并。我们可以通过调用一个辅助过程Merge(A, p, q, r)来完成合并，其中A是一个数组，p、q和r是数组下标，满足 p ≤ q < r。该过程假设子数组A[p..q]和A[q+1..r]都已排好序。它合并这两个子数组形成单一的已排好序的子数组并代替当前的子数组A[p..r]。

Merge(A, p, q, r)
1    n1 = q - p + 1
2    n2 = r - q
3    let L[1..n1+1] and R[1..n2+1] be new arrays
4    for (i = 1; i <= n1; i++)
5        L[i] = A[p+i-1]
6    for (j = 1; j <= n2; j++)
7        R[j] = A[q+j]
8    L[n1+1] = INF
9    R[n2+1] = INF
10    i = 1
11    j = 1
12    for (k = p; k <= r; k++)
13        if (L[i] <= R[j])
14            A[k] = L[i]
15            i = i + 1
16        else A[k] = R[j]
17            j = j + 1

   过程Merge的详细工作过程如下：

1. 第1行计算子数组A[p..q]的长度n1，第2行计算子数组A[q+1..r]的长度n2；
2. 在第3行，我们创建长度分别为n1+1和n2+1的数组L和R（"左"和"右"），每个数组中额外的位置将保存哨兵；
3. 第4-5行的for循环将子数组A[p..q]复制到L[1..n1]，第6-7行的for循环将子数组A[q+1..r]复制到R[1..n2]；
4. 第8-9行将哨兵放在数组L和R的末尾；
5. 第10-17行通过维持以下循环不变式，执行r-p+1个基本步骤：

   在开始第12-17行for循环的每次迭代时，子数组A[p..k-1]按从小到大的顺序包含L[1..n1+1]和R[1..n2+1]中的k-p个最小元素。进而，L[i]和R[j]是各自所在数组中未被复制回数组A的最小元素。

   现在我们可以把Merge作为归并排序算法中的一个子程序来用。下面的过程Merge-sort(A, p, r)排序子数组A[p..r]中的元素。若 p ≥ r，则该子数组最多有一个元素，所以已经排好序。否则，分解步骤简单地计算一个下标q，将A[p..r]分成两个子数组A[p..q]和A[q+1..r]。

Merge-sort(A, p, r)
1    if (p < r)
2        q = (p + r) / 2
3        Merge-sort(A, p, q)
4        Merge-sort(A, q+1, r)
5        Merge(A, p, q, r)

时间复杂度分析

   下面我们分析建立归并排序n个数的最坏情况运行时间T(n)的递归式。归并排序一个元素需要常量时间。当有n>1个元素时，我们分解运行时间如下：

   分解：分解步骤仅计算子数组的中间位置，需要常量时间，因此，D(n) = O(1)。

   解决：我们递归地求解两个规模均为n/2的子问题，将贡献2T(n/2)的运行时间。

   合并：我们已经注意到在一个具有n个元素的子数组上过程Merge需要O(n)的时间，所以C(n) = O(n)。

   则当n>1时，T(n) = 2T(n/2) + O(n)。递归式求解如下所示：

   

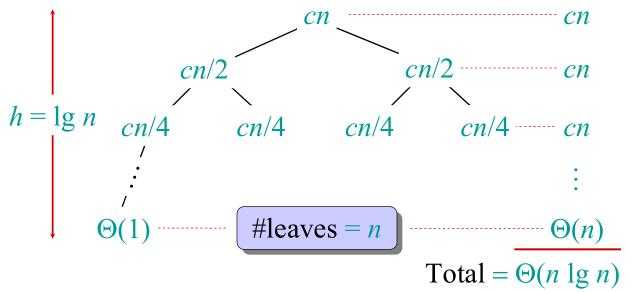
Exercise 2.3

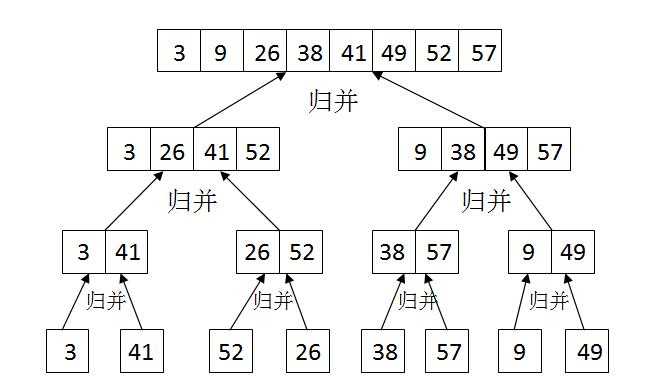
1.说明归并排序在数组A=<3, 41, 52, 26, 38, 57, 9, 49>上的操作。

【解答】如下图所示：

2.重写过程Merge，使之不使用哨兵，而是一旦数组L或R的所有元素均被复制回A就立刻停止，然后把另一个数组的剩余部分复制回A。

【解答】参考伪代码如下所示

Merge(A, p, q, r)
1    n1 = q - p + 1
2    n2 = r - q
3    let L[1..n1] and R[1..n2] be new arrays
4    for (i = 1; i <= n1; i++)
5        L[i] = A[p+i-1]
6    for (j = 1; j <= n2; j++)
7        R[j] = A[q+j]
8    i = 1
9    j = 1
10    k = p
11    while (i <= n1 && j <= n2)
12        if (L[i] <= R[j])
13            A[k++] = L[i++]
14        else A[k++] = R[j++]
15    while (i <= n1) A[k++] = L[i++]
16    while (j <= n2) A[k++] = R[j++]

3.使用数组归纳法证明：当n刚好是2的幂时，以下递归式的解是T(n) = nlgn。

   T(n)=2T(n/2)+n，若n=2^k，k>1，且T(2)=2。

【证明】略。

4.我们可以把插入排序表示为如下递归过程。为了排序A[1..n]，我们递归地排序A[1..n-1]，然后把A[n]插入已排序的数组A[1..n-1]。为插入排序的这个递归版本的最坏情况运行时间写一个递归式。

【解答】T(n) = T(n-1) + O(n) = O(n²)

5.回顾查找问题（参见练习2.1-3），注意到，如果序列A已排好序，就可以将该序列的中点与v进行比较。根据比较的结果，原序列中有一半就可以不用再做进一步的考虑了。二分查找算法重复这个过程，每次都将序列剩余部分的规模减半。为二分查找写出迭代或递归的伪代码。证明：二分查找的最坏情况运行时间为O(lgn)。

【解答】二分查找递归参考伪代码如下所示：

Binary-search(A, p, r, v)
1    if (p > r) return NIL
2    q = (p + r) / 2
3    if (A[q] == v) return q
4    else if (A[q] > v) 
5        return Binary-search(A, p, q-1)
6    else return Binary-search(A, q+1, r)

   迭代参考伪代码如下所示：

Binary-search(A, p, r, v)
1    while (p < r)
2        q = (p + r) / 2
3        if (A[q] == v) return q
4        else if (A[q] > v) r = q - 1
5        else p = q + 1
6    return NIL

   时间复杂度：T(n) = T(n/2) + O(1) = O(lgn)。

6.注意到插入排序中的过程Insertion-sort的第5-7行的while循环彩一种线性查找来（反向）扫描已排好序的子数组A[1..j-1]。我们可以使用二分查找（参见练习2.3-5）来把插入排序的最坏情况总运行时间改进到O(nlgn)吗？

【解答】不能。因为虽然能够减少查找的时间，但右移的时间是不能够减少的，依然是O(n)。

#7.描述一个运行时间为O(nlgn)的算法，给定n个整数的集合S和另一个整数x，该算法能确定S中是否存在两个其和刚好为x的元素。

【解答】先排序，然后用双指针分别从数组的头和尾遍历查找即可。

附录：归并排序代码示例

/**
 * 如果这段代码好用，那么它是xiaoxxmu写的
 * 否则，我也不知道是谁写的
 */
#include <stdio.h>
#include <stdlib.h>

void merge(int arr[], int p, int q, int r)
{ 
    int len1 = q - p + 1, len2 = r - q, i, j, k;
    int *L = (int *) malloc (len1 * sizeof(int)); 
    int *R = (int *) malloc (len2 * sizeof(int)); 
    for (i = 0; i < len1; i++)
        L[i] = arr[p+i]; 
    for (j = 0; j < len2; j++)
        R[j] = arr[q+j+1]; 
    i = 0, j = 0, k = p; 
    while (i < len1 && j < len2)
    {
        if (L[i] < R[j]) arr[k++] = L[i++]; 
        else arr[k++] = R[j++]; 
    }
    while (i < len1) arr[k++] = L[i++]; 
    while (j < len2) arr[k++] = R[j++]; 
}

void merge_sort(int arr[], int p, int r)
{
    if (p < r)
    {
        int q = (p + r) / 2; 
        merge_sort(arr, p, q); 
        merge_sort(arr, q+1,r); 
        merge(arr, p, q, r); 
    }
}

int main(int argc, char *argv[])
{
    int arr[] = {3, 41, 52, 26, 38, 57, 9, 49, 44}; 
    int length = (sizeof arr) / (sizeof arr[0]); 
    merge_sort(arr, 0, length - 1); 
    for (int i = 0; i < length; i++)
    {
        if (i == 0) printf("%d", arr[i]); 
        else printf(" %d", arr[i]); 
    }
    printf("\\n"); 
    return 0; 
}