数值算法：无约束优化之一维搜索方法之二分法牛顿法割线法

Posted 2020-08-22 宏斌PKUCIS

 

1、二分法（一阶导）

二分法是利用目标函数的一阶导数来连续压缩区间的方法，因此这里除了要求 f 在 [a₀,b₀] 为单峰函数外，还要去 f(x) 连续可微。

（1）确定初始区间的中点 x⁽⁰⁾=(a₀+b₀)/2 。然后计算 f(x) 在 x⁽⁰⁾ 处的一阶导数 f\'(x⁽⁰⁾)， 如果 f\'(x⁽⁰⁾) >0 , 说明极小点位于 x⁽⁰⁾ 的左侧，也就是所，极小点所在的区间压缩为[a₀,x⁽⁰⁾]；反之，如果 f\'(x⁽⁰⁾) <0，说明极小点位于x⁽⁰⁾的右侧，极小点所在的区间压缩为[x⁽⁰⁾，b₀]；如果f\'(x⁽⁰⁾) = 0，说明就是函数 f(x) 的极小点。

（2）根据新的区间构造x⁽¹⁾，以此来推，直到f\'(x^(k)) = 0，停止。

可见经过N步迭代之后，整个区间的总压缩比为（1/2）^N，这比黄金分割法和斐波那契数列法的总压缩比要小。

1 #ifndef _BINARYSECTION_H_
2 #define _BINARYSECTION_H_
3 
4 typedef float (* PtrOneVarFunc)(float x);
5 void BinarySectionMethod(float a, float b, PtrOneVarFunc fi, float epsilon);
6 
7 #endif

 1 #include<iostream>
 2 #include<cmath>
 3 #include "BinarySection.h"
 4 
 5 using namespace std;
 6 
 7 void BinarySectionMethod(float a, float b, PtrOneVarFunc tangent, float epsilon)
 8 {
 9     float a0,b0,middle;
10     int k;
11     k = 1;
12     a0 = a;
13     b0 = b;
14     middle = ( a0 + b0 )/2;
15     
16     while( abs(tangent(middle)) - epsilon > 0 )
17     {
18 #ifdef _DEBUG
19         cout<<k++<<"th iteration:x="<<middle<<",f\'("<<middle<<")="<<tangent(middle)<<endl;
20 #endif
21  
22         if( tangent(middle) > 0)
23         {
24             b0 = middle;
25         }
26         else
27         {
28             a0 = middle;
29         }
30         middle =( a0+b0)/2;
31     }
32     
33     cout<<k<<"th iteration:x="<<middle<<",f\'("<<middle<<")="<<tangent(middle)<<endl;
34 }

 1 #include<iostream>
 2 #include "BinarySection.h"
 3 
 4 
 5 float TangentFunctionofOneVariable(float x)
 6 {
 7     return 14*x-5;//7*x*x-5*x+2;
 8 }
 9 
10 int main()
11 {
12     BinarySectionMethod(-50, 50, TangentFunctionofOneVariable, 0.001);
13     return 0;
14 }

1th iteration:x=0,f\'(0)=-5
2th iteration:x=25,f\'(25)=345
3th iteration:x=12.5,f\'(12.5)=170
4th iteration:x=6.25,f\'(6.25)=82.5
5th iteration:x=3.125,f\'(3.125)=38.75
6th iteration:x=1.5625,f\'(1.5625)=16.875
7th iteration:x=0.78125,f\'(0.78125)=5.9375
8th iteration:x=0.390625,f\'(0.390625)=0.46875
9th iteration:x=0.195312,f\'(0.195312)=-2.26562
10th iteration:x=0.292969,f\'(0.292969)=-0.898438
11th iteration:x=0.341797,f\'(0.341797)=-0.214844
12th iteration:x=0.366211,f\'(0.366211)=0.126953
13th iteration:x=0.354004,f\'(0.354004)=-0.0439453
14th iteration:x=0.360107,f\'(0.360107)=0.0415039
15th iteration:x=0.357056,f\'(0.357056)=-0.0012207
16th iteration:x=0.358582,f\'(0.358582)=0.0201416
17th iteration:x=0.357819,f\'(0.357819)=0.00946045
18th iteration:x=0.357437,f\'(0.357437)=0.00411987
19th iteration:x=0.357246,f\'(0.357246)=0.00144958
20th iteration:x=0.357151,f\'(0.357151)=0.000114441

 

2、牛顿法（二阶导）

前提：f 在 [a₀,b₀] 为单峰函数， 且[a₀,b₀] 在极小点附近，不能离的太远否则可能无法收敛。

这里进一步要求f(x)连续二阶可微。对于函数 f(x) 上一点 x^(k)，我们可以使用泰勒公式构造一个多项式函数 q(x)=f(x^(k))+f\'(x^(k))(x-x^(k))+1/2 * f\'\'(x^(k))(x-x^(k))²,对 f（x）在 x^(k) 附近进行局部二次拟合，q(x)可以看为f(x)的（在x^(k)附近的局部）近似（当f(x)为二次函数时，q(x)=f(x)），因此求f(x)的极小点可以转化为求q(x)的极小点。

0=q\'(x)=f\'(x^(k))+f\'\'(x^(k))(x-x^(k))  =>   x = x^(k)  -  f\'(x^(k))/f\'\'(x^(k))  因此可以选择 x^(k+1) = x^(k)  -  f\'(x^(k))/f\'\'(x^(k))

牛顿法能够不断地迫使目标函数f(x)的一阶导数趋于0。x^(k+1)由g（x^(k)）的切线产生：

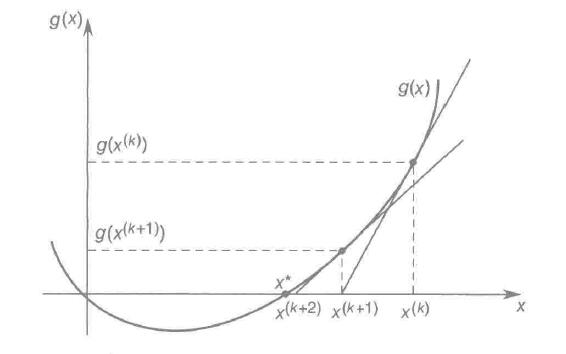
x^(k+1)为g（x^(k)）的切线与x轴交点。随着x^(k) -> x^*,  g(x)->0。（g(x)为f(x)的近似）

 

注意1：牛顿法不需要计算函数值，但需要计算一阶导数和二阶导数值，且要求 f\'\'(x)>0，如果f\'\'(x)<0，则可能存在从 x^(k) 到 x^(k+1)反向调整，收敛到极大点，即越来越偏离极小点。

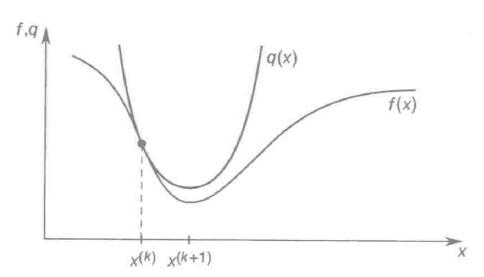
f\'\'(x^(k))>0, x^(k)->x^*

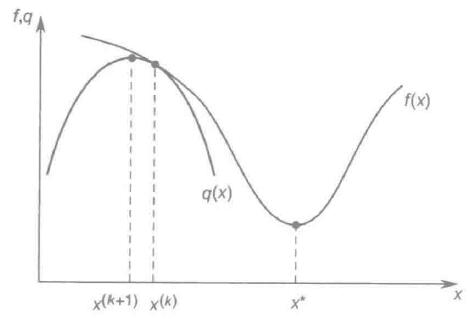
f\'\'(x^(k))<0, x^(k)远离x^*

注意2：如果初始x^(k)的调整幅度太大可能会导致x的调整序列在极小点左右波动。

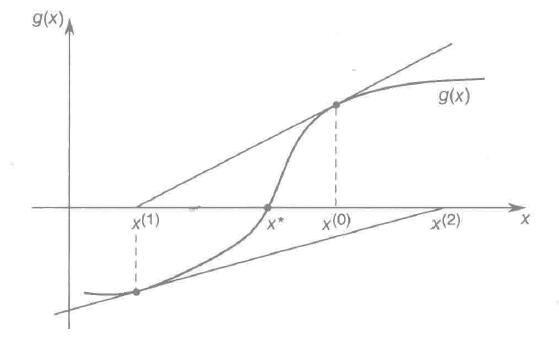
初始点g\'(x⁽⁰⁾)/g\'\'(x⁽⁰⁾)太大，造成算法失效

 1 #ifndef _NEWTON_H_
 2 #define _NEWTON_H_
 3 
 4 #define NEWTON_ZERO  0.0001
 5 
 6 typedef float (* PtrOneVarFunc)(float x);
 7 
 8 
 9 
10 void NewtonMethod(float x0, PtrOneVarFunc oneorderderivative, PtrOneVarFunc twoorderderivative, float epsilon);
11 
12 
13 #endif

 1 #include<iostream>
 2 #include<cmath>
 3 #include "Newton.h"
 4 
 5 using namespace std;
 6 
 7 void NewtonMethod(float x0, PtrOneVarFunc oneorderderivative, PtrOneVarFunc twoorderderivative, float epsilon)
 8 {
 9     float xk,newtonstep;
10     int k;
11     k = 0;
12     xk = x0;
13 
14     while( abs(oneorderderivative(xk)) - epsilon > 0)
15     {
16 
17 #ifdef _DEBUG
18         cout<<k<<"th iteration xk="<<xk<<",f\'("<<xk<<")="<<oneorderderivative(xk)<<endl;
19 #endif
20         k++;
21 
22         newtonstep = twoorderderivative(xk);
23         if(abs(newtonstep) - NEWTON_ZERO < 0)
24         {
25             cout<<"f\'\'("<<xk<<")=0, algorithms terminate!"<<endl;
26             return ;
27         }
28 
29         newtonstep = oneorderderivative(xk) / newtonstep;
30         xk = xk - newtonstep;
31     }
32 
33     cout<<k<<"th iteration xk="<<xk<<",f\'("<<xk<<")="<<oneorderderivative(xk)<<endl;
34 }

#include<iostream>
#include "Newton.h"


float OneOrderDerivative(float x)
{
    return (14*x-5);//f(x)=7*x*x-5*x+2;
}


float TwoOrderDerivative(float x)
{
    return 14;//f\'\'(x)=14;
}

int main()
{
    NewtonMethod(-109.23, OneOrderDerivative, TwoOrderDerivative, 0.001);
    return 0;
}

0th iteration xk=-109.23,f\'(-109.23)=-1534.22
1th iteration xk=0.35714,f\'(0.35714)=-4.57764e-05

（3）割线法

前提：f 在 [a₀,b₀] 为单峰函数， 且[a₀,b₀] 在极小点附近，不能离的太远否则可能无法收敛。

 牛顿法需要f(x)的二阶导数，如果二阶导数不存在，可以采用不同点的一阶导数对其近似，如 f\'\'(x^(k))=(f\'(x^(k))-f\'(x^(k-1)))/(x^(k)-x^(k-1)),将其带入牛顿迭代公式，可以得到新的迭代公式：

 x^(k+1) = x^(k)  -  f\'(x^(k))  *  (x^(k)-x^(k-1)) /(f\'(x^(k))-f\'(x^(k-1)))   <=>   x^(k+1) = ( f\'(x^(k))x^(k-1)  - f\'(x^(k-1)) x^(k)  )    /   (    f\'(x^(k))  -  f\'(x^(k-1))  )

这个方法需要两个初始点 x^(-1)和x⁽⁰⁾,可以看出割线法不需要计算函数值f(x^(k))，二阶导数值f\'\'(x^(k))，它使用x^(k)和x^(k-1)之间的割线产生x^(k+1)：

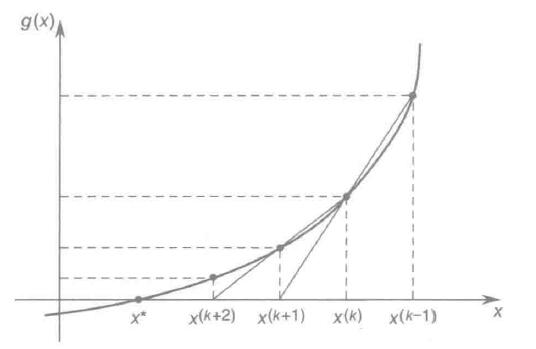
x^(k+1)由过x^(k)和x^(k-1)的割线产生

 1 #ifndef _SECANT_H_
 2 #define _SECANT_H_
 3 
 4 #define SECANT_ZERO  0.1
 5 
 6 typedef float (* PtrOneVarFunc)(float x);
 7 
 8 
 9 
10 void SecantMethod(float x0, float x_1, PtrOneVarFunc oneorderderivative, float epsilon);
11 
12 
13 #endif

 1 #include<iostream>
 2 #include<cmath>
 3 #include "Secant.h"
 4 
 5 using namespace std;
 6 
 7 void SecantMethod(float x_1, float x0, PtrOneVarFunc oneorderderivative, float epsilon)
 8 {
 9     float xk,xk_1,t1,t_1,tk;
10     int k;
11     k = 0;
12     xk = x0;
13     xk_1 = x_1;
14 
15     if(xk - xk_1 < SECANT_ZERO)
16     {
17         cout<<"x0 == x_1,algorithm terminate."<<endl;
18         return;
19     }
20 
21     while( abs(oneorderderivative(xk)) - epsilon > 0)
22     {
23 #ifdef _DEBUG
24         cout<<k<<"th iteration xk_1="<<xk_1<<",f\'("<<xk_1<<")="<<oneorderderivative(xk_1)<<",xk="<<xk<<",f\'("<<xk<<")="<<oneorderderivative(xk)<<endl;
25 #endif
26 
27         k++;
28 
29         t1 = oneorderderivative(xk);
30         t_1 = oneorderderivative(xk_1);
31 
32         tk = xk;
33         xk = (t1*xk_1 - t_1*xk)/(t1-t_1);
34         xk_1 = tk;
35     }
36 
37         cout<<k<<"th iteration xk_1="<<xk_1<<",f\'("<<xk_1<<")="<<oneorderderivative(xk_1)<<",xk="<<xk<<",f\'("<<xk<<")="<<oneorderderivative(xk)<<endl;
38 
39 }

 1 #include<iostream>
 2 #include "Secant.h"
 3 
 4 
 5 float OneOrderDerivative(float x)
 6 {
 7     return (14*x-5);//f(x)=7*x*x-5*x+2;
 8 }
 9 
10 
11 int main()
12 {
13     SecantMethod(-109.23, -20, OneOrderDerivative, 0.001);
14     return 0;
15 }

0th iteration xk_1=-109.23,f\'(-109.23)=-1534.22,xk=-20,f\'(-20)=-285
1th iteration xk_1=-20,f\'(-20)=-285,xk=0.357142,f\'(0.357142)=-1.03116e-05

（4）拟抛物线插值法

迭代算法跟割线法类似，不同点为使用三个点的函数值近似公式中的两个一阶导数。