原创地址: http://www.cnblogs.com/Alandre/ (泥沙砖瓦浆木匠),须要转载的,保留下! Thanks
“应注意到一个析取命题的对立命题是由该析取命题各部分的对立内容构成的一个合取命题” ——奥卡姆的威廉著。《逻辑学论文》
Written In The Font
I like maths when i was young,but I need to record them. So I am writing with some demos of Python
Content
If two events, A and B are independent then the joint probability is
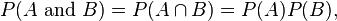
For example, if two coins are flipped the chance of both being heads is
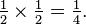
In Python
A = set([1,2,3,4,5]) B = set([2,4,3,5,6]) C = set([4,6,7,4,2,1]) print(A & B & C)
Output:
| {2, 4} |
# & find the objects the same in Set
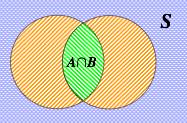
If either event A or event B or both events occur on a single performance of an experiment this is called the union of the events A and B denoted as:
.
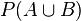If two events are mutually exclusive then the probability of either occurring is
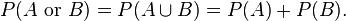
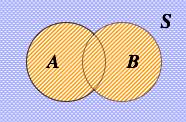
For example, the chance of rolling a 1 or 2 on a six-sided die is
In Python
A = set([1,2,3,4,5]) B = set([2,4,3,5,6]) C = set([4,6,7,4,2,1]) print(A | B | C)
Output:
|
{1, 2, 3, 4, 5, 6, 7} |
# | find all the objects the set has
If the events are not mutually exclusive then
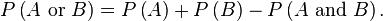
Proved
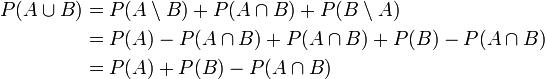
For example:
Let’s use Python to show u an example about devil‘s bones (骰子,不是 魔鬼的骨头哈
)
A = set([1,2,3,4,5,6]) # the all results of devil‘s bones B = set([2,4,3]) # the A event results C = set([4,6]) # the B event results P_B = 1/2 P_C = 1/3 D = B | C print(D) P_D = 2/3 print(P_D == (P_B+P_C - 1/6))
Output:
|
{2, 3, 4, 6} |
Let me show u some others :
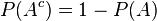
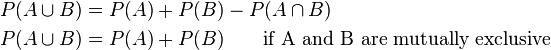
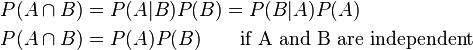
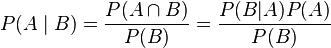
If u r tired , please have a tea , or look far to make u feel better.If u r ok, Go on!
Conditional probability is the probability of some event A, given the occurrence of some other event B. Conditional probability is written:
,
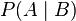Some authors, such as De Finetti, prefer to introduce conditional probability as an axiom of probability:
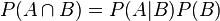①
Given two events A and B from the sigma-field of a probability space with P(B) > 0, the conditional probability of A given Bis defined as the quotient of the probability of the joint of events A and B, and the probability of B:
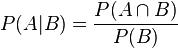②
the ①② expressions are the same. Maybe u can remember one , the other will be easy to be coverted.So I am going to tell an excemple to let u remmeber it(them):
“the phone has a power supply (B), the phone can be used to call others(A).”
One → 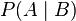: When the phone has a full power supply , u can call others.
Two →P(B): has a power supply
Three = One + Two → U can call others about your love with others.
do u remember it?
Editor‘s Note
“路漫漫其修远兮,吾将上下而求索”
The Next
cya soon. We meet a big mess called The total probability and Bayes .
The total probability
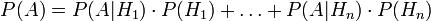
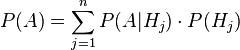
Bayes (Thomas, 1702-1761,) ;
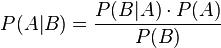
if u wanna talk with me , add the follow:
