梯度下降算法笔记
Posted coskaka
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了梯度下降算法笔记相关的知识,希望对你有一定的参考价值。
今天课上主要讲的是梯度下降算法。
上一次老师留了梯度下降算法求解线性回归的作业。大部分用java和C++实现的。
笔记也主要来自课程ppt,老师课程的ppt也主要参考的斯坦福吴恩达老师的讲义。
梯度下降法(英语:Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。[来自维基百科]
1 __author__ = \'Oscar_Yang\' 2 #-*- coding= utf-8 -*- 3 """ 4 实现线性回归参数预测 5 """ 6 class GD(object): 7 def __init__(self, e=0.03,m=5,rate=0.02,maxIterations=10000):#初始化属性 8 self.e = e 9 self.m = m 10 self.rate = rate 11 self.maxIterations=maxIterations 12 """ 13 梯度下降拟合函数 14 """ 15 def fit(self,X,y,data): 16 self.theta = np.ones(data.shape[1]) 17 self.cost_ = [] 18 for i in range(0, self.maxIterations): 19 output = self.predict(X) 20 errors = (y - output) 21 cost = (errors ** 2).sum() / 2.0 22 self.cost_.append(cost) 23 if cost < self.e: 24 break 25 else: 26 gradient = np.dot(X.T,errors) / self.m 27 self.theta = self.theta + self.rate * gradient 28 return self 29 """ 30 normal equation 31 """ 32 @staticmethod 33 def fit_equation(X,y): 34 xTx = X.T.dot(X) 35 XtX = np.linalg.inv(xTx) 36 XtX_xT = XtX.dot(X.T) 37 theta = XtX_xT.dot(y) 38 return theta 39 40 41 def predict(self, X): 42 return np.dot(X,self.theta) 43 @classmethod 44 def cal_time(self): 45 return time.clock() 46 if __name__ == \'__main__\': 47 48 import pandas as pd 49 import numpy as np 50 import time 51 import matplotlib.pyplot as plt 52 53 data = pd.read_table("shuju1.txt") 54 traindata0 = pd.DataFrame(np.ones(data.shape[0])) 55 traindata1 = data.ix[:, 0:-1] 56 traindata = pd.concat([traindata0, traindata1], axis=1) 57 traindata_label = data.ix[:, -1] 58 """ 59 normal equation 60 """ 61 real_theta = GD(m=5,rate=0.01).fit_equation(traindata,traindata_label) 62 print("精确参数:",real_theta) 63 print("_____________________________________") 64 fig,ax=plt.subplots(nrows=1,ncols=3,figsize=(18,6)) 65 start_time = GD.cal_time() 66 ada1 = GD(m=5,rate=0.01).fit(traindata, traindata_label, data=data) 67 end_time = GD.cal_time() 68 during_time=end_time-start_time 69 70 print("rate={}时候的参数为:{}".format(ada1.rate,ada1.theta)) 71 print("迭代次数:",len(ada1.cost_)) 72 print("耗时:",during_time) 73 ax[0].plot(range(1,len(ada1.cost_)+1),np.log10(ada1.cost_),marker="o") 74 ax[0].set_xlabel("Epochs") 75 ax[0].set_ylabel(\'log(sum_squ_err)\') 76 title = "rate:", ada1.rate 77 ax[0].set_title(title) 78 79 start_time=GD.cal_time() 80 ada2 = GD(rate=0.03,m=5).fit(traindata, traindata_label, data=data) 81 end_time = GD.cal_time() 82 print("_____________________________________") 83 print("rate={}时候的参数为:{}".format(ada2.rate, ada2.theta)) 84 print("迭代次数:",len(ada2.cost_)) 85 print("耗时:",end_time-start_time) 86 87 ax[1].plot(range(1, len(ada2.cost_)+1), np.log10(ada2.cost_), marker="o") 88 ax[1].set_xlabel("Epochs") 89 ax[1].set_ylabel(\'log(sum_squ_err)\') 90 title="rate:",ada2.rate 91 ax[1].set_title(title) 92 93 94 95 start_time=GD.cal_time() 96 ada3 = GD( rate=0.06, m=5).fit(traindata, traindata_label, data=data) 97 end_time=GD.cal_time() 98 # print(ada3.theta) 99 print("_____________________________________") 100 print("rate={}时候的参数为:{}".format(ada3.rate, ada3.theta)) 101 print("迭代次数:",len(ada3.cost_)) 102 print("耗时:",end_time-start_time) 103 104 ax[2].plot(range(1, len(ada3.cost_) + 1), np.log10(ada3.cost_), marker="o") 105 ax[2].set_xlabel("Epochs") 106 ax[2].set_ylabel(\'log(sum_squ_err)\') 107 title = "rate:", ada3.rate 108 ax[2].set_title(title) 109 110 plt.show()
精确参数: [ 1.75789474 1.21684211 -0.50526316]
_____________________________________
rate=0.01时候的参数为:[ 1.75789374 1.21684043 -0.50526106]
迭代次数: 10000
耗时: 7.593358084384351
_____________________________________
rate=0.03时候的参数为:[ 1.75789474 1.21684211 -0.50526316]
迭代次数: 10000
耗时: 7.8287073625201655
_____________________________________
rate=0.06时候的参数为:[ 1.75789474 1.21684211 -0.50526316]
迭代次数: 10000
耗时: 7.562434044109619
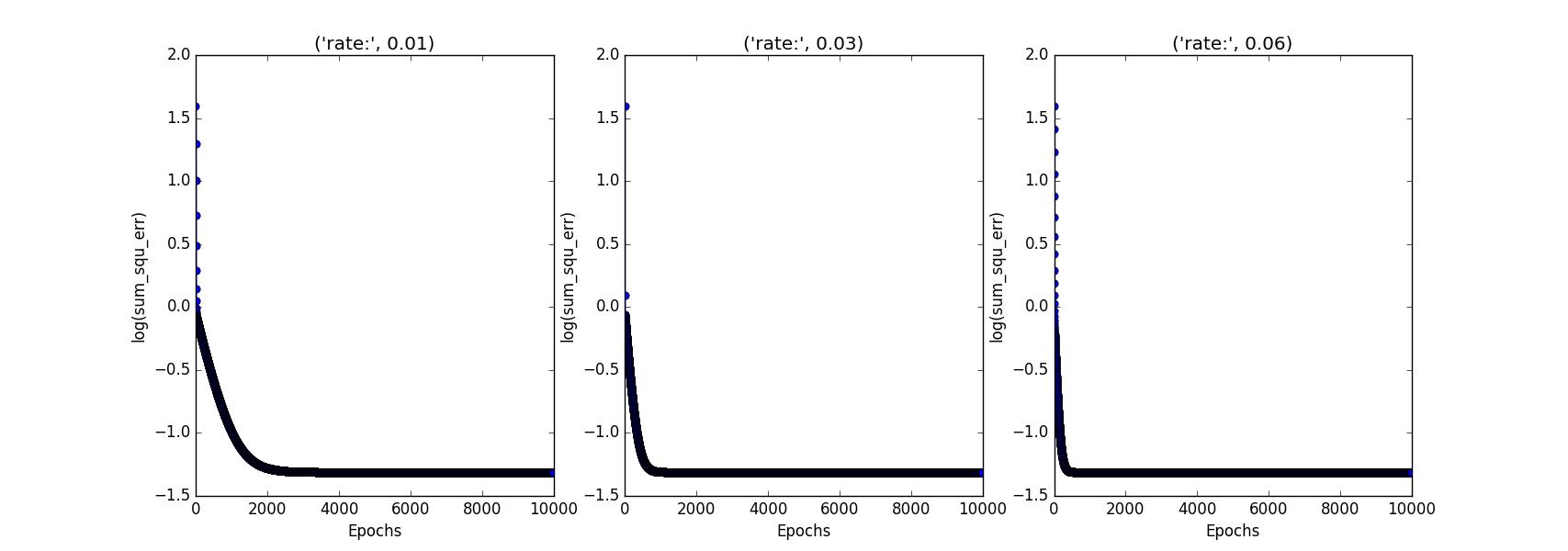
以上是关于梯度下降算法笔记的主要内容,如果未能解决你的问题,请参考以下文章