Coursera Machine Learning : Regression 评估性能

Posted 2020-08-21 One-Way

评估性能

　　评估损失

　　1、Training Error

　　首先要通过数据来训练模型，选取数据中的一部分作为训练数据.

　　

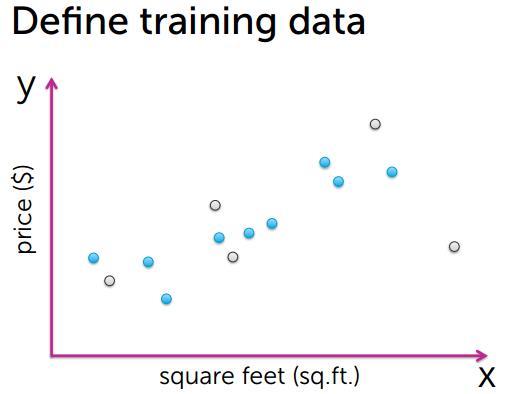
　　损失函数可以使用绝对值误差或者平方误差等方法来计算，这里使用平方误差的方法，即：　(y-f(x))²

　　使用此方法计算误差，然后计算所有数据点，并求平均数。

　　

　　Training Error 越小，模型越好？答案是否定的，下面看看Training Error 和模型复杂度的关系。

　　

　　

　　

　　

　　

 

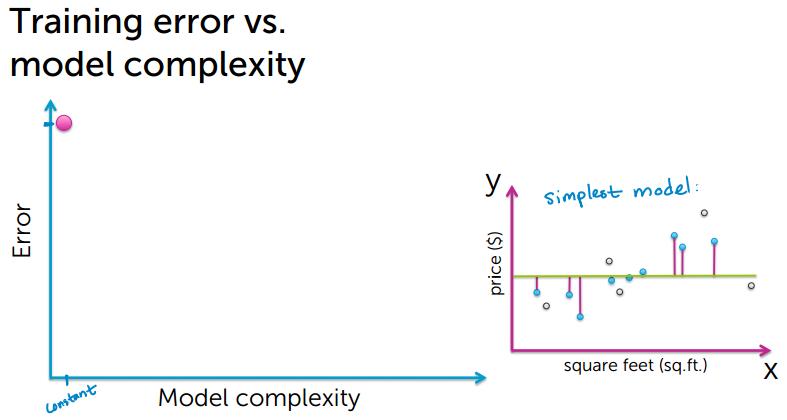
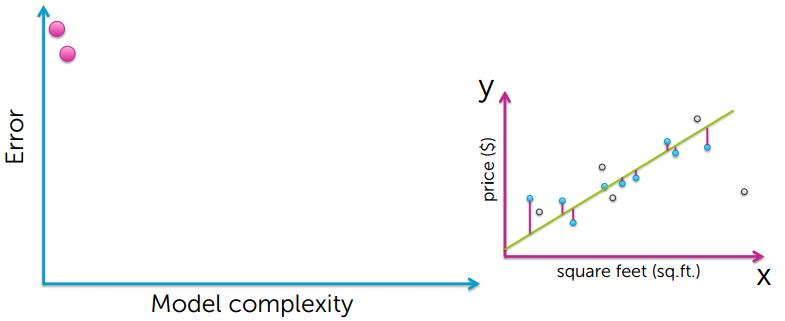
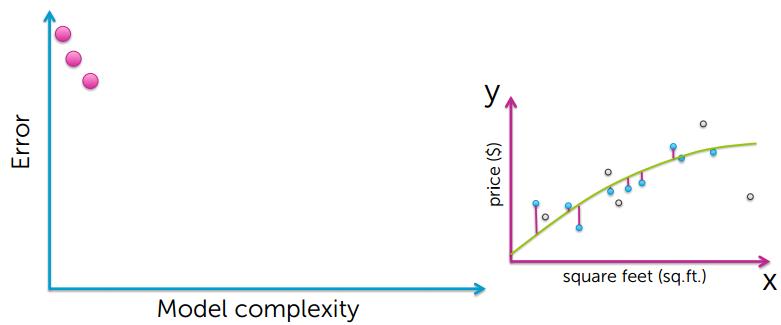
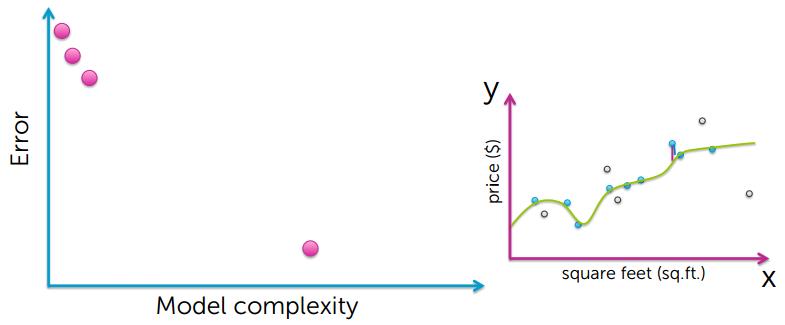
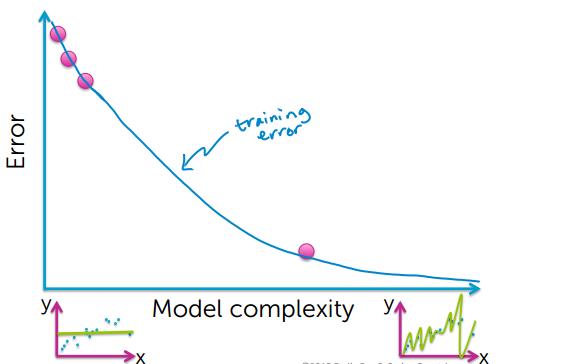
　　从上的的图可以看出，要想使training error越小，模型就会变得越复杂，然后出现了过拟合的现象

　　很有可能训练数据中有个别异常数据点，如果过度拟合所有的数据点，就会导致模型过拟合，并不能很好的对房价进行预测；

　　training error 小，并不能说明是个很好的预测。

　　

　　

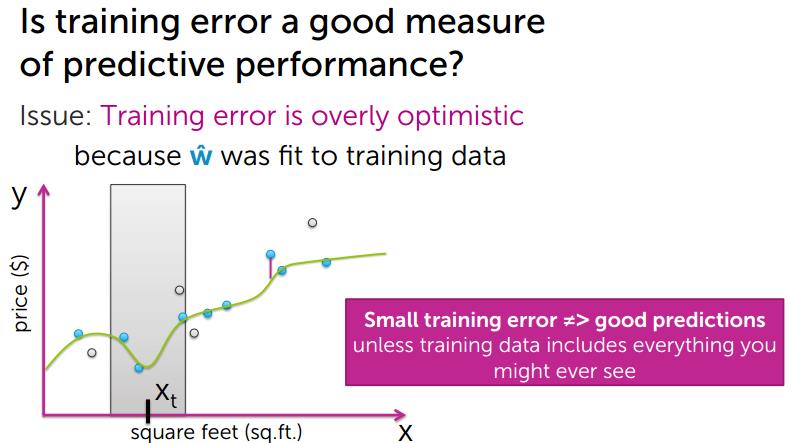
　　2、Generalization (true) error 真实误差

　　首先说明的一点是这个值是不能计算出来的；

　　计算真实误差，首先需要知道真实值，训练数据中的数据不一定就代表真实值，不过可以通过训练数据中的平均值来估算出来。

　　比如，计算房子A的房价，找出所有与A类似的房子求出房价，计算平均值。来估算房价。

　　

　　下面来看看真实误差和模型复杂度的关系：

　　图像中的真实值，参考图像中颜色变浅的中间位置

　　

　　

　　

　　

　　

　　

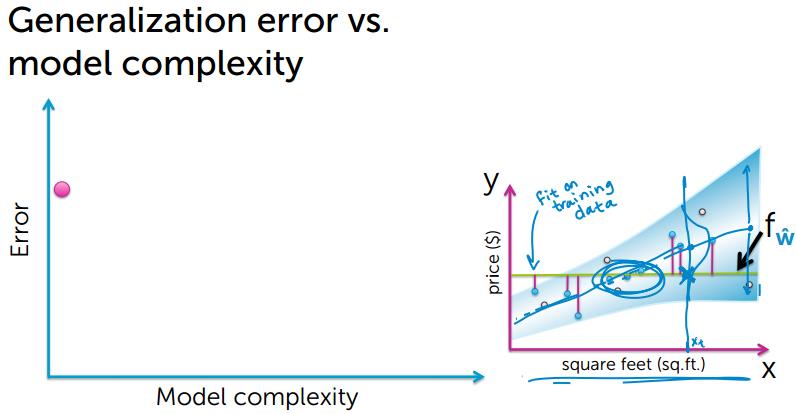
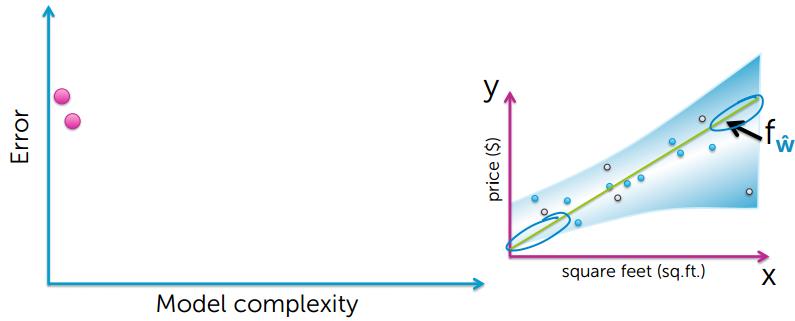
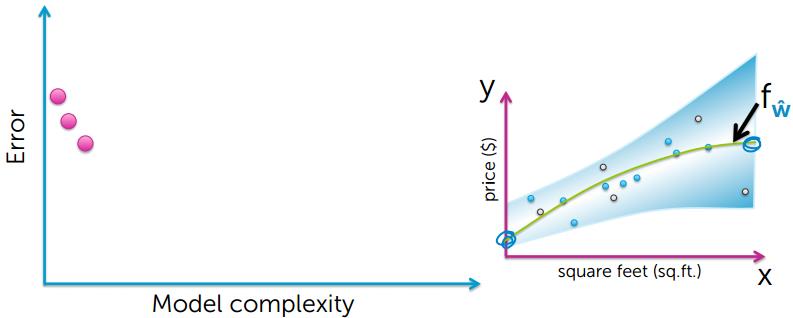
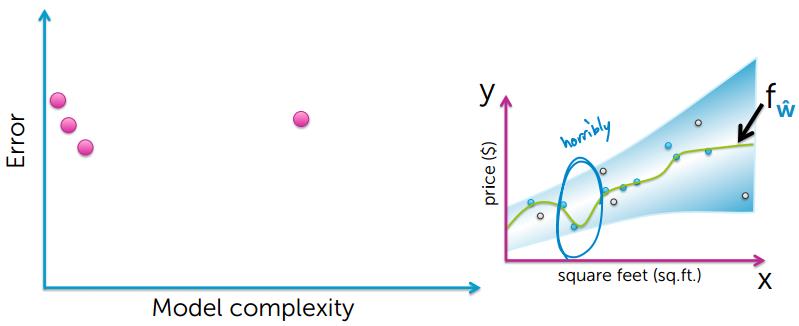
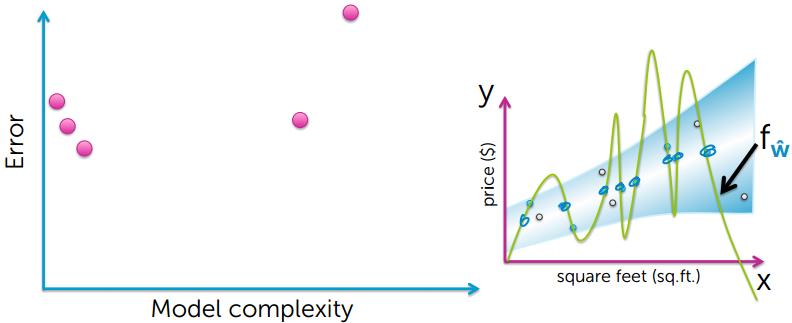
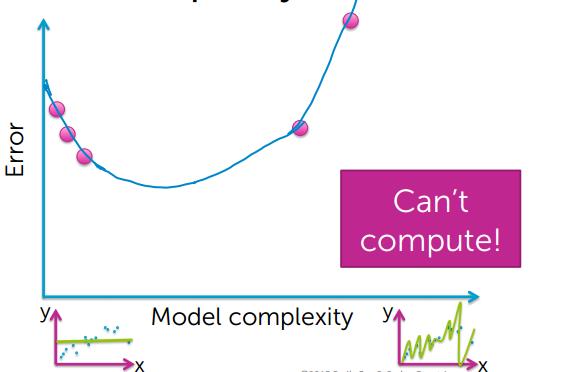
　　通过上图可以看出，模型简单和模型过度复杂，都不能很好的对数据进行预测

　　

　　3、Test Error

　　Test Error 和 True Error 接近，Test Error的测试数据来自测试数据集。

　　

　　

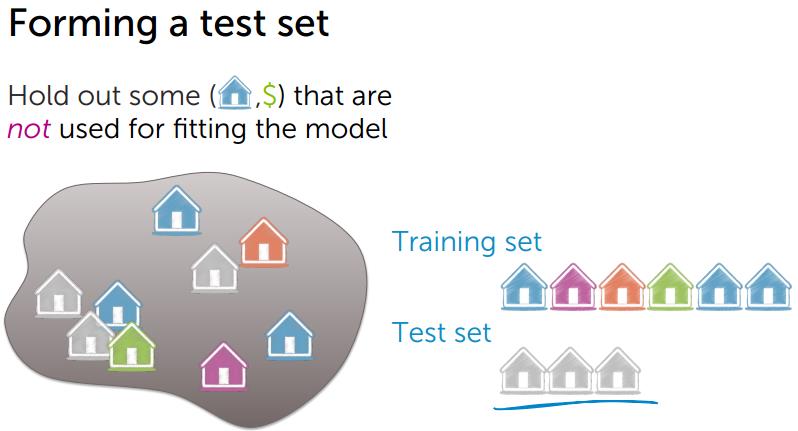
　　对测试数据集进行计算误差，计算方法和Training Error类似。

　　

　　

　　Training, true, & test error 和 模型复杂度的比较：

　　test error 在 true error的周边波动，接近true error的值。

　　

　　从上图中可以看出，总结出过拟合的判断：

　　模型中存在估计参数w\'

　　　　1. training error(w) < training error(w\')

　　　　2. true error(w) > true error (w\')

　　 说明w过拟合

 

　　误差的3个来源

　　　Noise, Bias, Variance

　　1、Noise 噪声

　　　　固有的，不可约减的

　　

　

　　2、Bias 偏差

　　偏差是预测值（估计值）的期望与真实值之间的差距，偏差越大，越偏离真实数据。

　　

 

　　

 

　　

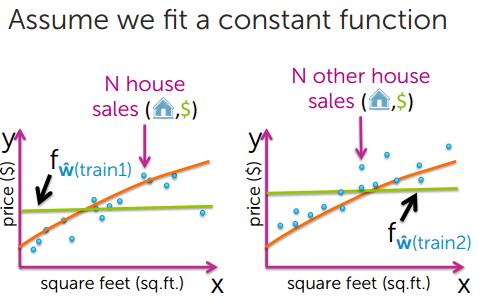
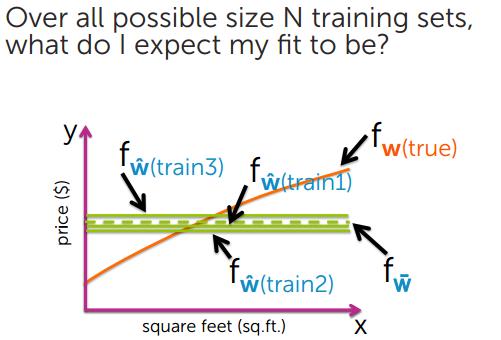
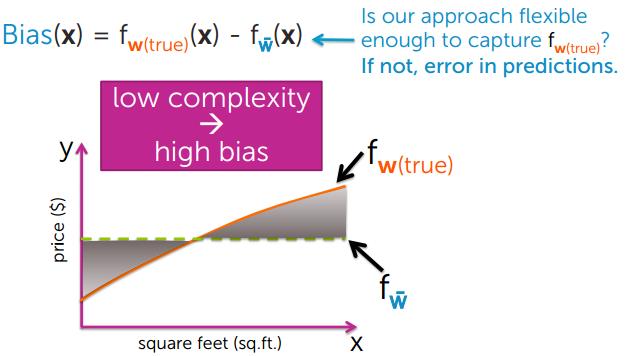
　　模型越简单，偏差越大

　　

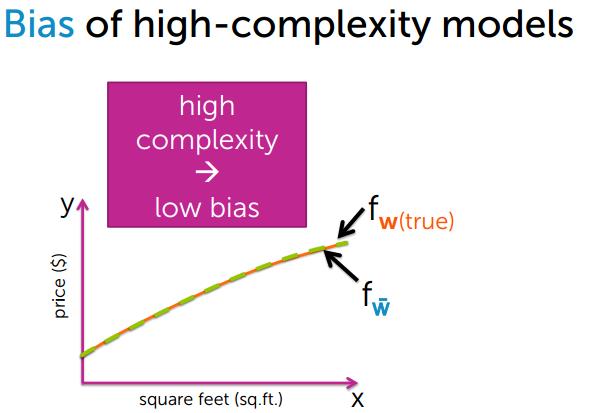
　　模型越复杂，偏差越小

 

　　3、Variance 方差

　　描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散

　　

　　

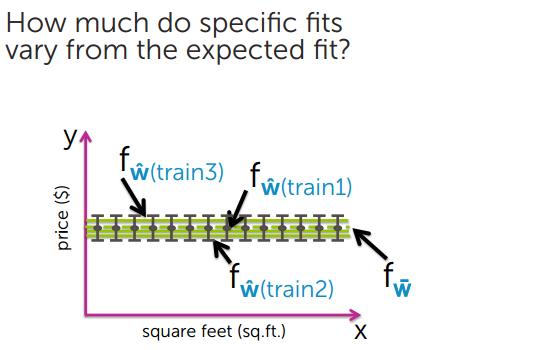
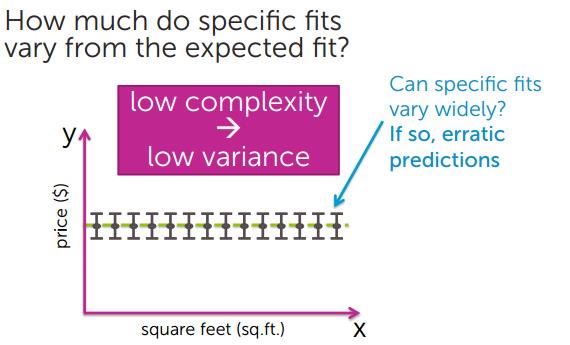
　　模型简单，方差小

　　

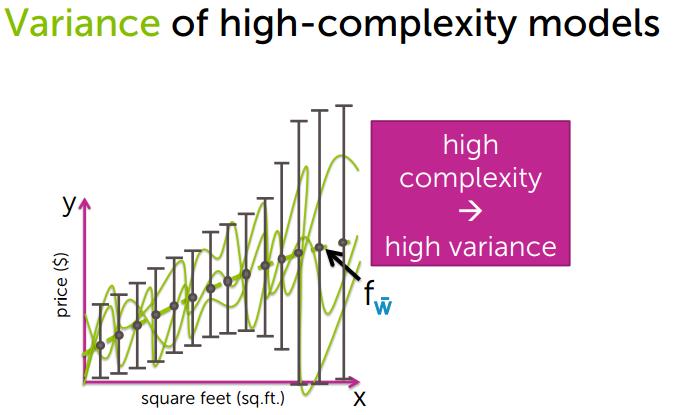
　　模型复杂，方差大

　　

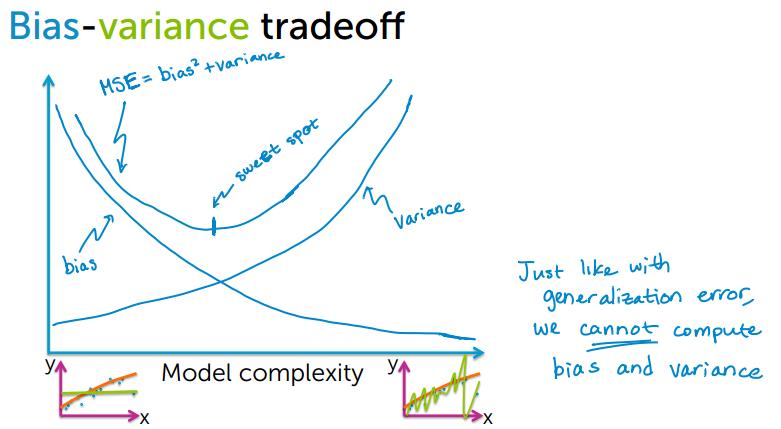
 　　偏差和方差权衡，偏差和方差不能计算

　　

　　

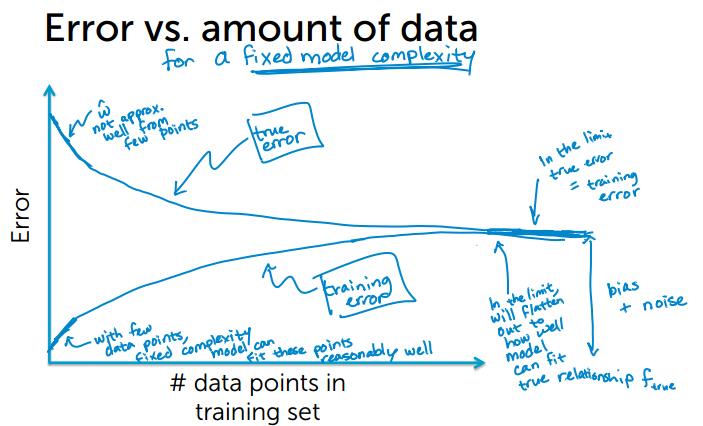
　　training error和测试数据量的关系，固定的模型复杂度，少量数据拟合更好，误差会更小;随着数据量的增大，误差也随之增大，会达到一个临界点与true error 相等。

　　true error 和测试数据量的关系，固定的模型复杂度，少量的数据的true error会更大;随着数据量的增大，误差也随之减小，会到达一个临界点与training error 相等。