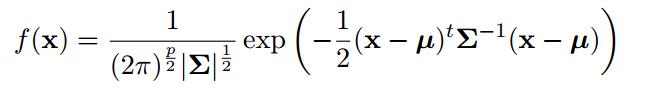怎么利用r语言做em算法估计混合双参数指数分布的数值模拟

Posted 2023-03-21

参考技术A 建议你先看一下这本书:
Modeling Survival Data Using Frailty Models

chap 2. Some Parametric Methods
2.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.2 Exponential Distribution . . . . . . . . . . . . . . . . . . . 20
2.3 Weibull Distribution . . . . . . . . . . . . . . . . . . . . . 21
2.4 Extreme Value Distributions . . . . . . . . . . . . . . . . 23
2.5 Lognormal . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.6 Gamma . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.7 Loglogistic . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.8 Maximum Likelihood Estimation . . . . . . . . . . . . . 30
2.9 Parametric Regression Models

chap 6. Estimation Methods for Shared Frailty Models
6.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . 105
6.2 Inference for the Shared Frailty Model . . . . . . . . . . 106
6.3 The EM Algorithm . . . . . . . . . . . . . . . . . . . . . . . 108
6.4 The Gamma Frailty Model . . . . . . . . . . . . . . . . . . . 110
6.5 The Positive Stable Frailty Model . . . . . . . . . . . . . . 111
6.6 The Lognormal Frailty Model . . . . . . . . . . . . . . . . . 113
6.6.1 Application to Seizure Data . . . . . . . . . . . . . . . 113
6.7 Modified EM (MEM) Algorithm for Gamma Frailty Models 114
6.8 Application

然后用最基本的package "survival"
并参考你的模型可能用到的一些functions:
survreg(formula, data, weights, subset,na.action, dist="weibull",....)
survreg.distributions include "weibull", "exponential", "gaussian",
"logistic","lognormal" and "loglogistic"
frailty(x, distribution="gamma", ...)
distribution: either the gamma, gaussian or t distribution may be specified.
frailty.gamma(x, sparse = (nclass > 5), theta, df, eps = 1e-05,
method = c("em","aic", "df", "fixed"),...)本回答被提问者和网友采纳

大数据部落R语言实现：混合正态分布EM最大期望估计法

原文链接：http://tecdat.cn/?p=4815

 

因为近期在分析数据时用到了EM最大期望估计法这个算法，在参数估计中也用到的比较多。然而，发现国内在R软件上实现高斯混合分布的EM的实例并不多，大多数是关于1到2个高斯混合分布的实现，不易于推广，因此这里分享一下自己编写的k个高斯混合分布的EM算法实现请大神们多多指教。并结合EMCluster包对结果进行验算。

      本文使用的密度函数为下面格式：

---

?

   对应的函数原型为 em.norm(x,means,covariances,mix.prop)

x为原数据，means为初始均值，covariances为数据的协方差矩阵，mix.prop为混合参数初始值。

使用的数据为MASS包里面的synth.te数据的前两列

x <- synth.te[,-3]

首先安装需要的包，并读取原数据。

install.packages("MASS")

library(MASS)

install.packages("EMCluster")

library(EMCluster)

install.packages("ggplot2")

library(ggplot2)

Y=synth.te[,c(1:2)]

qplot(x=xs, y=ys, data=Y) 

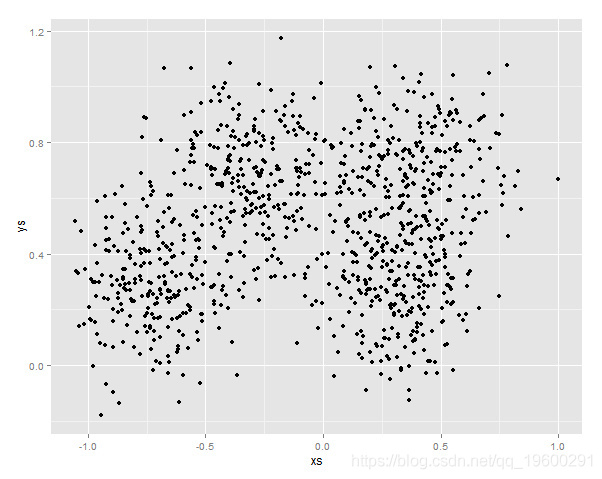
然后绘制相应的变量相关图：

?

从图上我们可以大概估计出初始的平均点为(-0.7,0.4) (-0.3,0.8)(0.5,0.6)

当然 为了试验的严谨性，我可以从两个初始均值点的情况开始估计

首先输入初始参数：

mustart = rbind(c(-0.5,0.3),c(0.4,0.5))    

covstart = list(cov(Y), cov(Y))

probs = c(.01, .99)

 

然后编写em.norm函数，注意其中的clusters值需要根据不同的初始参数进行修改，

em.norm = function(X,mustart,covstart,probs)



  params = list(mu=mustart, var=covstart, probs=probs)   

  clusters = 2 

  tol=.00001

  maxits=100

  showits=T

  require(mvtnorm)



  N = nrow(X)

  mu = params$mu

  var = params$var

  probs = params$probs

  

  

  ri = matrix(0, ncol=clusters, nrow=N)         

  ll = 0                                        

  it = 0                                         

  converged = FALSE                            

  

  if (showits)                                 

    cat(paste("Iterations of EM:", "\\n"))

  

  while (!converged & it < maxits)  

    probsOld = probs

    

    llOld = ll

    riOld = ri

    

   

    # Compute responsibilities

    for (k in 1:clusters)

      ri[,k] = probs[k] * dmvnorm(X, mu[k,], sigma = var[[k]], log=F)

    

    ri = ri/rowSums(ri)

    

  

    rk = colSums(ri)                             

    probs = rk/N

    for (k in 1:clusters)

      varmat = matrix(0, ncol=ncol(X), nrow=ncol(X))         

      for (i in 1:N)

        varmat = varmat + ri[i,k] * X[i,]%*%t(X[i,])

      

      mu[k,] = (t(X) %*% ri[,k]) / rk[k]

      var[[k]] =  varmat/rk[k] - mu[k,]%*%t(mu[k,])

      ll[k] = -.5 * sum( ri[,k] * dmvnorm(X, mu[k,], sigma = var[[k]], log=T) )

    

    ll = sum(ll)

    

     

    parmlistold =  c(llOld, probsOld)            

    parmlistcurrent = c(ll, probs)             

    it = it + 1

    if (showits & it == 1 | it%%5 == 0)         

      cat(paste(format(it), "...", "\\n", sep = ""))

    converged = min(abs(parmlistold - parmlistcurrent)) <= tol

  

  

  clust = which(round(ri)==1, arr.ind=T)       

  clust = clust[order(clust[,1]), 2]           

  out = list(probs=probs, mu=mu, var=var, resp=ri, cluster=clust, ll=ll)

 

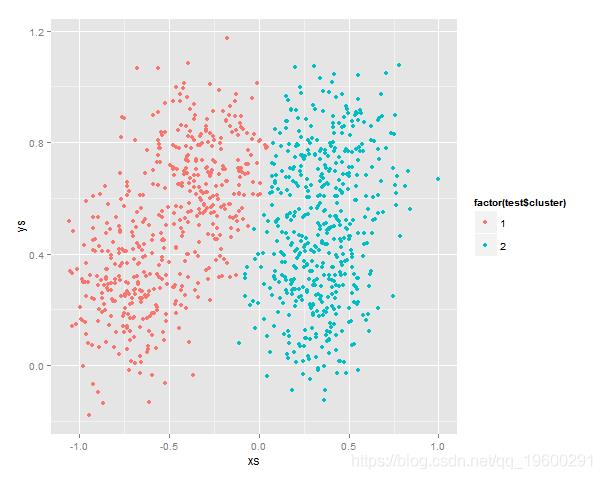
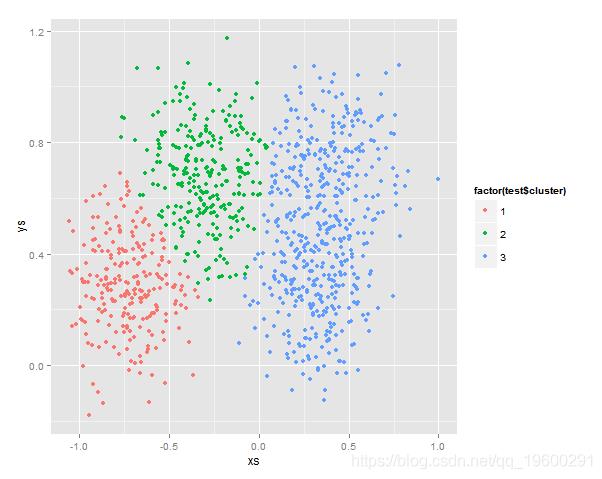
结果，可以用图像化来表示：

qplot(x=xs, y=ys, data=Y) 

ggplot(aes(x=xs, y=ys), data=Y) +

   geom_point(aes(color=factor(test$cluster))) 

?

?

 

 

 类似的其他情况这里不呈现了，另外r语言提供了EMCluster包可以比较方便的实现EM进行参数估计和结果的误差分析。

ret <- init.EM(Y, nclass = 2)

em.aic(x=Y,emobj=list(pi = ret$pi, Mu = ret$Mu, LTSigma = ret$LTSigma))#计算结果的AIC

通过比较不同情况的AIC，我们可以筛选出适合的聚类数参数值。

有问题欢迎下方留言！

大数据部落 -中国专业的第三方数据服务提供商，提供定制化的一站式数据挖掘和统计分析咨询服务

统计分析和数据挖掘咨询服务：y0.cn/teradat（咨询服务请联系官网客服）

?QQ：3025393450

?

【服务场景】  

科研项目; 公司项目外包;线上线下一对一培训;数据采集;学术研究;报告撰写;市场调查。

【大数据部落】提供定制化的一站式数据挖掘和统计分析咨询

欢迎选修我们的R语言数据分析挖掘必知必会课程！