第五次作业

Posted 2020-08-20

3-3  证明：I(X;Y)=H(X)-H(X|Y)

 

：

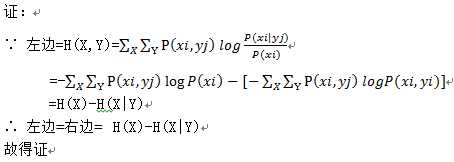
3-9   没有冗余的信源还能不能压缩？为什么？

   答：不能进行无损压缩，可以进行有损压缩。

3-10  不相关的信源还能不能压缩？为什么？

  答：至少可以进行有损压缩。因为“等概”未必“不相关”，例如：对正弦信号的均匀取样值。

3-12  等概率分布的信源还能不能压缩？为什么？你能举例说明吗？

     答：至少是可以进行有损压缩的

3-15  有人认为：“图像的负片（黑白颠倒）比正片更容易压缩”。你同意他的观点吗？为什么？

    答：不同意。图像的正负片的熵是相同的，即该图像的冗余度是相同的，所以压缩的容易程度是一样的。

3-16  有人认为：“相关的信源是非等概率分布的”。你同意他的观点吗？为什么？

  答：同意。因为我们知道只要信源不是等概率分布，就存在着数据压缩的可能性。