排序---归并排序

Posted 2020-08-20 Pearl_zhen

写在前面的话：

一枚自学Java和算法的工科妹子。

• 算法学习书目：算法（第四版） Robert Sedgewick
• 算法视频教程：Coursera  Algorithms Part1&2

本文是根据《算法（第四版）》的个人总结，如有错误，请批评指正。

一、归并排序介绍

    归并排序（Mergesort）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

    归并过程：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到aux[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到aux[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到aux中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

    分治法解题的一般步骤：

（1）分解，将要解决的问题划分成若干规模较小的同类问题；

（2）求解，当子问题划分得足够小时，用较简单的方法解决；

（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

 

二、原地归并的抽象方法

    将涉及的所有元素复制到一个辅助数组中，再把归并的结果放会原数组中。

图1 原地归并的抽象方法的轨迹

 1 private static void merge(Comparable[] a,int lo, int mid, int hi) {
 2         // precondition: a[lo .. mid] and a[mid+1 .. hi] are sorted subarrays
 3         assert isSorted(a, lo, mid);
 4         assert isSorted(a, mid+1, hi);
 5 
 6         // 将a[lo..hi]复制到aux[lo..hi],注意这里的aux[]是全局变量，在方法外已经声明。
 7         for (int k = lo; k <= hi; k++) {
 8             aux[k] = a[k]; 
 9         }
10 
11         // 归并回a[lo..hi]
12         int i = lo, j = mid+1;
13         for (int k = lo; k <= hi; k++) {
14             if      (i > mid)              a[k] = aux[j++];
15             else if (j > hi)               a[k] = aux[i++];
16             else if (less(aux[j], aux[i])) a[k] = aux[j++];
17             else                           a[k] = aux[i++];
18         }
19 
20         // postcondition: a[lo .. hi] is sorted
21         assert isSorted(a, lo, hi);
22     }

 三、自顶向下的归并排序

 

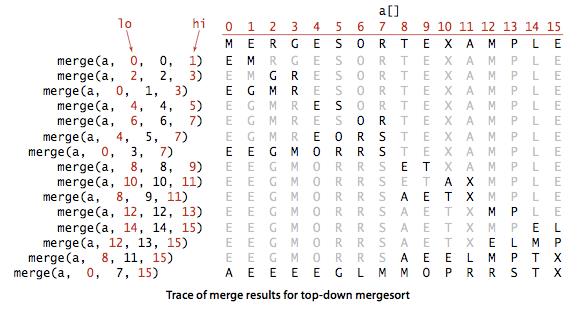
图2 自顶向下的归并排序的调用轨迹

 1 public class Merge {
 2 
 3     // This class should not be instantiated.
 4     private Merge() { }
 5     private static Comparable[] aux ;
 6 
 7    // stably merge a[lo .. mid] with a[mid+1 ..hi] using aux[lo .. hi]
 8     private static void merge(Comparable[] a, int lo, int mid, int hi) {
 9         // precondition: a[lo .. mid] and a[mid+1 .. hi] are sorted subarrays
10         assert isSorted(a, lo, mid);
11         assert isSorted(a, mid+1, hi);
12 
13         // copy to aux[]
14         for (int k = lo; k <= hi; k++) {
15             aux[k] = a[k]; 
16         }
17 
18         // merge back to a[]
19         int i = lo, j = mid+1;
20         for (int k = lo; k <= hi; k++) {
21             if      (i > mid)              a[k] = aux[j++];
22             else if (j > hi)               a[k] = aux[i++];
23             else if (less(aux[j], aux[i])) a[k] = aux[j++];
24             else                           a[k] = aux[i++];
25         }
26 
27         // postcondition: a[lo .. hi] is sorted
28         assert isSorted(a, lo, hi);
29     }
30 
31     public static void sort(Comparable[] a) {
32         aux = new Comparable[a.length];
33         sort(a, 0, a.length-1);
34         assert isSorted(a);
35     }
36 
37     // mergesort a[lo..hi] using auxiliary array aux[lo..hi]
38     private static void sort(Comparable[] a, int lo, int hi) {
39         if (hi <= lo) return;
40         int mid = lo + (hi - lo) / 2;
41         sort(a, lo, mid);
42         sort(a, mid + 1, hi);
43         merge(a, lo, mid, hi);
44     }
45 
46     // is v < w ?
47     private static boolean less(Comparable v, Comparable w) {
48         return v.compareTo(w) < 0;
49     }
50         
51     private static boolean isSorted(Comparable[] a) {
52         return isSorted(a, 0, a.length - 1);
53     }
54 
55     private static boolean isSorted(Comparable[] a, int lo, int hi) {
56         for (int i = lo + 1; i <= hi; i++)
57             if (less(a[i], a[i-1])) return false;
58         return true;
59     }
60 
61     // print array to standard output
62     private static void show(Comparable[] a) {
63         for (int i = 0; i < a.length; i++) {
64             StdOut.println(a[i]);
65         }
66     }
67 }

自顶向下归并排序的性能分析：

对于长度为N的任意数组，自顶向下的归并排序需要1/2NlgN至NlgN次比较和6NlgN次访问数组；

（1）比较次数为1/2NlgN至NlgN次的证明（三种证明方法）：

• Proof 1：

         

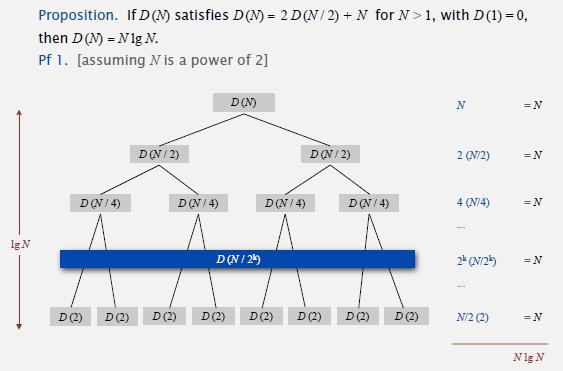
• Proof 2：

         

• Proof 3：

         

（2）访问数组为6NlgN次证明：每次归并最多需要访问数组次数为6N，其中2N次用来复制，2N次用来比较，2N次用来将比较出来的元素移动会a[].

  四、自顶向下的归并排序

 

 

图3 自底向上的归并排序的归并结果

 1 public class MergeBU {
 2 
 3     // This class should not be instantiated.
 4     private MergeBU() { }
 5     private static Comparable[] aux;
 6 
 7     // stably merge a[lo..mid] with a[mid+1..hi] using aux[lo..hi]
 8     private static void merge(Comparable[] a, int lo, int mid, int hi) {
 9 
10         // copy to aux[]
11         for (int k = lo; k <= hi; k++) {
12             aux[k] = a[k]; 
13         }
14 
15         // merge back to a[]
16         int i = lo, j = mid+1;
17         for (int k = lo; k <= hi; k++) {
18             if      (i > mid)              a[k] = aux[j++];  // this copying is unneccessary
19             else if (j > hi)               a[k] = aux[i++];
20             else if (less(aux[j], aux[i])) a[k] = aux[j++];
21             else                           a[k] = aux[i++];
22         }
23 
24     }
25 
26 
27     public static void sort(Comparable[] a) {
28         int n = a.length;
29         aux = new Comparable[n];
30         for (int len = 1; len < n; len *= 2) {
31             for (int lo = 0; lo < n-len; lo += len+len) {
32                 merge(a, lo, lo+len-1, Math.min(lo+len+len-1, n-1));
33             }
34         }
35         assert isSorted(a);
36     }
37     
38     // is v < w ?
39     private static boolean less(Comparable v, Comparable w) {
40         return v.compareTo(w) < 0;
41     }
42 
43     private static boolean isSorted(Comparable[] a) {
44         for (int i = 1; i < a.length; i++)
45             if (less(a[i], a[i-1])) return false;
46         return true;
47     }
48 
49     // print array to standard output
50     private static void show(Comparable[] a) {
51         for (int i = 0; i < a.length; i++) {
52             StdOut.println(a[i]);
53         }
54     }
55 }

自底向上归并排序的性能分析：

对于长度为N的任意数组，自底向上的归并排序需要1/2NlgN至NlgN次比较和6NlgN次访问数组；

 

 五、归并排序优化

（1）节省时间（不将元素复制到辅助数组）：在递归调用的每个层次交换数组和辅助数组的角色；

（2）将小数组排序改用插入排序；

（3）比较左边数组的最大值和右边数组的最小值的大小，如果小于，则不需要在归并。

优化后的代码如下：

  1 public class MergeX {
  2     private static final int CUTOFF = 7;  // cutoff to insertion sort
  3 
  4     // This class should not be instantiated.
  5     private MergeX() { }
  6 
  7     private static void merge(Comparable[] src, Comparable[] dst, int lo, int mid, int hi) {
  8 
  9         // precondition: src[lo .. mid] and src[mid+1 .. hi] are sorted subarrays
 10         assert isSorted(src, lo, mid);
 11         assert isSorted(src, mid+1, hi);
 12 
 13         int i = lo, j = mid+1;
 14         for (int k = lo; k <= hi; k++) {
 15             if      (i > mid)              dst[k] = src[j++];
 16             else if (j > hi)               dst[k] = src[i++];
 17             else if (less(src[j], src[i])) dst[k] = src[j++];   // to ensure stability
 18             else                           dst[k] = src[i++];
 19         }
 20 
 21         // postcondition: dst[lo .. hi] is sorted subarray
 22         assert isSorted(dst, lo, hi);
 23     }
 24 
 25     private static void sort(Comparable[] src, Comparable[] dst, int lo, int hi) {
 26         // if (hi <= lo) return;
 27         if (hi <= lo + CUTOFF) { 
 28             insertionSort(dst, lo, hi);
 29             return;
 30         }
 31         int mid = lo + (hi - lo) / 2;
 32         sort(dst, src, lo, mid);
 33         sort(dst, src, mid+1, hi);
 34 
 35         // if (!less(src[mid+1], src[mid])) {
 36         //    for (int i = lo; i <= hi; i++) dst[i] = src[i];
 37         //    return;
 38         // }
 39 
 40         // using System.arraycopy() is a bit faster than the above loop
 41         if (!less(src[mid+1], src[mid])) {
 42             System.arraycopy(src, lo, dst, lo, hi - lo + 1);
 43             return;
 44         }
 45 
 46         merge(src, dst, lo, mid, hi);
 47     }
 48 
 49 
 50     public static void sort(Comparable[] a) {
 51         Comparable[] aux = a.clone();
 52         sort(aux, a, 0, a.length-1);  
 53         assert isSorted(a);
 54     }
 55 
 56     // sort from a[lo] to a[hi] using insertion sort
 57     private static void insertionSort(Comparable[] a, int lo, int hi) {
 58         for (int i = lo; i <= hi; i++)
 59             for (int j = i; j > lo && less(a[j], a[j-1]); j--)
 60                 exch(a, j, j-1);
 61     }
 62 
 63     // exchange a[i] and a[j]
 64     private static void exch(Object[] a, int i, int j) {
 65         Object swap = a[i];
 66         a[i] = a[j];
 67         a[j] = swap;
 68     }
 69 
 70     // is a[i] < a[j]?
 71     private static boolean less(Comparable a, Comparable b) {
 72         return a.compareTo(b) < 0;
 73     }
 74 
 75     // is a[i] < a[j]?
 76     private static boolean less(Object a, Object b, Comparator comparator) {
 77         return comparator.compare(a, b) < 0;
 78     }
 79 
 80     public static void sort(Object[] a, Comparator comparator) {
 81         Object[] aux = a.clone();
 82         sort(aux, a, 0, a.length-1, comparator);
 83         assert isSorted(a, comparator);
 84     }
 85 
 86     private static void merge(Object[] src, Object[] dst, int lo, int mid, int hi, Comparator comparator) {
 87 
 88         // precondition: src[lo .. mid] and src[mid+1 .. hi] are sorted subarrays
 89         assert isSorted(src, lo, mid, comparator);
 90         assert isSorted(src, mid+1, hi, comparator);
 91 
 92         int i = lo, j = mid+1;
 93         for (int k = lo; k <= hi; k++) {
 94             if      (i > mid)                          dst[k] = src[j++];
 95             else if (j > hi)                           dst[k] = src[i++];
 96             else if (less(src[j], src[i], comparator)) dst[k] = src[j++];
 97             else                                       dst[k] = src[i++];
 98         }
 99 
100         // postcondition: dst[lo .. hi] is sorted subarray
101         assert isSorted(dst, lo, hi, comparator);
102     }
103 
104 
105     private static void sort(Object[] src, Object[] dst, int lo, int hi, Comparator comparator) {
106         // if (hi <= lo) return;
107         if (hi <= lo + CUTOFF) { 
108             insertionSort(dst, lo, hi, comparator);
109             return;
110         }
111         int mid = lo + (hi - lo) / 2;
112         sort(dst, src, lo, mid, comparator);
113         sort(dst, src, mid+1, hi, comparator);
114 
115         // using System.arraycopy() is a bit faster than the above loop
116         if (!less(src[mid+1], src[mid], comparator)) {
117             System.arraycopy(src, lo, dst, lo, hi - lo + 1);
118             return;
119         }
120 
121         merge(src, dst, lo, mid, hi, comparator);
122     }
123 
124     // sort from a[lo] to a[hi] using insertion sort
125     private static void insertionSort(Object[] a, int lo, int hi, Comparator comparator) {
126         for (int i = lo; i <= hi; i++)
127             for (int j = i; j > lo && less(a[j], a[j-1], comparator); j--)
128                 exch(a, j, j-1);
129     }
130 
131     private static boolean isSorted(Comparable[] a) {
132         return isSorted(a, 0, a.length - 1);
133     }
134 
135     private static boolean isSorted(Comparable[] a, int lo, int hi) {
136         for (int i = lo + 1; i <= hi; i++)
137             if (less(a[i], a[i-1])) return false;
138         return true;
139     }
140 
141     private static boolean isSorted(Object[] a, Comparator comparator) {
142         return isSorted(a, 0, a.length - 1, comparator);
143     }
144 
145     private static boolean isSorted(Object[] a, int lo, int hi, Comparator comparator) {
146         for (int i = lo + 1; i <= hi; i++)
147             if (less(a[i], a[i-1], comparator)) return false;
148         return true;
149     }
150 
151     // print array to standard output
152     private static void show(Object[] a) {
153         for (int i = 0; i < a.length; i++) {
154             StdOut.println(a[i]);
155         }
156     }
157 }

 

六、归并排序总结

    归并排序是一种渐进最优的基于比较的排序算法，归并排序在最坏的情况下的比较次数为~NlgN，这是其他排序算法复杂度的上限。详细证明可以见算法（第四版）pp.177-178

 

作者： 邹珍珍（Pearl_zhen）

出处： http://www.cnblogs.com/zouzz/

声明：本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出 原文链接 如有问题， 可邮件（[e-mail]）咨询.