FZU 1759 欧拉函数 降幂公式

Posted 2020-08-20 半根毛线code

 

Description

 

Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).

Input

There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.

 

Output

For each testcase, output an integer, denotes the result of A^B mod C.

 

Sample Input

3 2 4
2 10 1000

Sample Output

1
24

Hint

 

Source

FZU 2009 Summer Training IV--Number Theory

 

题意：A^B mod C

题解：

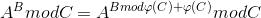
降幂公式 phi() 为欧拉函数

 

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #define ll __int64
 5 #define mod 10000000007
 6 using namespace std;
 7 char a[1000006];
 8 ll x,z;
 9 ll quickpow(ll x,ll y,ll z)
10 {
11     ll ans=1;
12     while(y)
13     {
14         if(y&1)
15             ans=ans*x%z;
16         x=x*x%z;
17         y>>=1;
18     }
19     return ans;
20 }
21 ll phi(ll n)
22 {
23     ll i,rea=n;
24     for(i=2;i*i<=n;i++)
25     {
26         if(n%i==0)
27         {
28             rea=rea-rea/i;
29             while(n%i==0)
30                 n/=i;
31          }
32     }
33     if(n>1)
34         rea=rea-rea/n;
35     return rea;
36 }
37 int main()
38 {
39     while(scanf("%I64d %s %I64d",&x,a,&z)!=EOF)
40     {
41         ll len=strlen(a);
42         ll p=phi(z);
43         ll ans=0;
44         for(ll i=0;i<len;i++)
45             ans=(ans*10+a[i]-\'0\')%p;
46         ans+=p;
47         printf("%I64d\\n",quickpow(x,ans,z));
48     }
49     return 0;
50 }