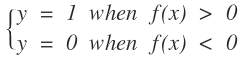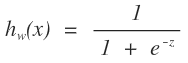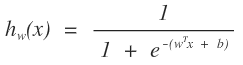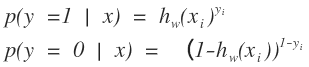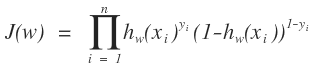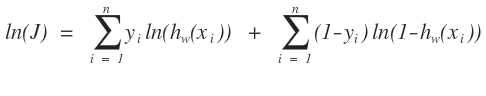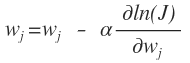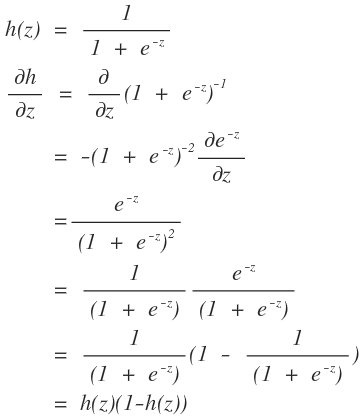从另一个视角看待逻辑回归

Posted 2020-08-20

摘要

逻辑回归是用在分类问题中，而分类为题有存在两个比较大的方向：分类的结果用数值表是，比如1和0(逻辑回归采用的是这种)，或者-1和1(svm采用的)，还有一种是以概率的形式来反应，通过概率来说明此样本要一个类的程度即概率。同时分类问题通过适用的场合可以分为：离散和连续，其中决策树分类，贝叶斯分类都是适用离散场景，但是连续场景也可以处理，只是处理起来比较麻烦，而逻辑回归就是用在连续特征空间中的，并把特征空间中的超平面的求解转化为概率进行求解，然后通过概率的形式来找给出分类信息，最后设置一个阈值来进行分类。

逻辑回归

问题描述

首先我们要明白，我们要解决的问题：给你一批数据，这一批数据特征都是连续的，并且我还知道这批数据的分类信息(x,y),x为特征，y为类别，取值为：0或者1。我们想干什么，想通过这批数据，然后再

给一个新的数据x，这个数据只存在特征，不存在类别，我们想给出分类的结果，是0还是1。下面为了方便，我们以二维空间的点为例进行说明。

解决策略

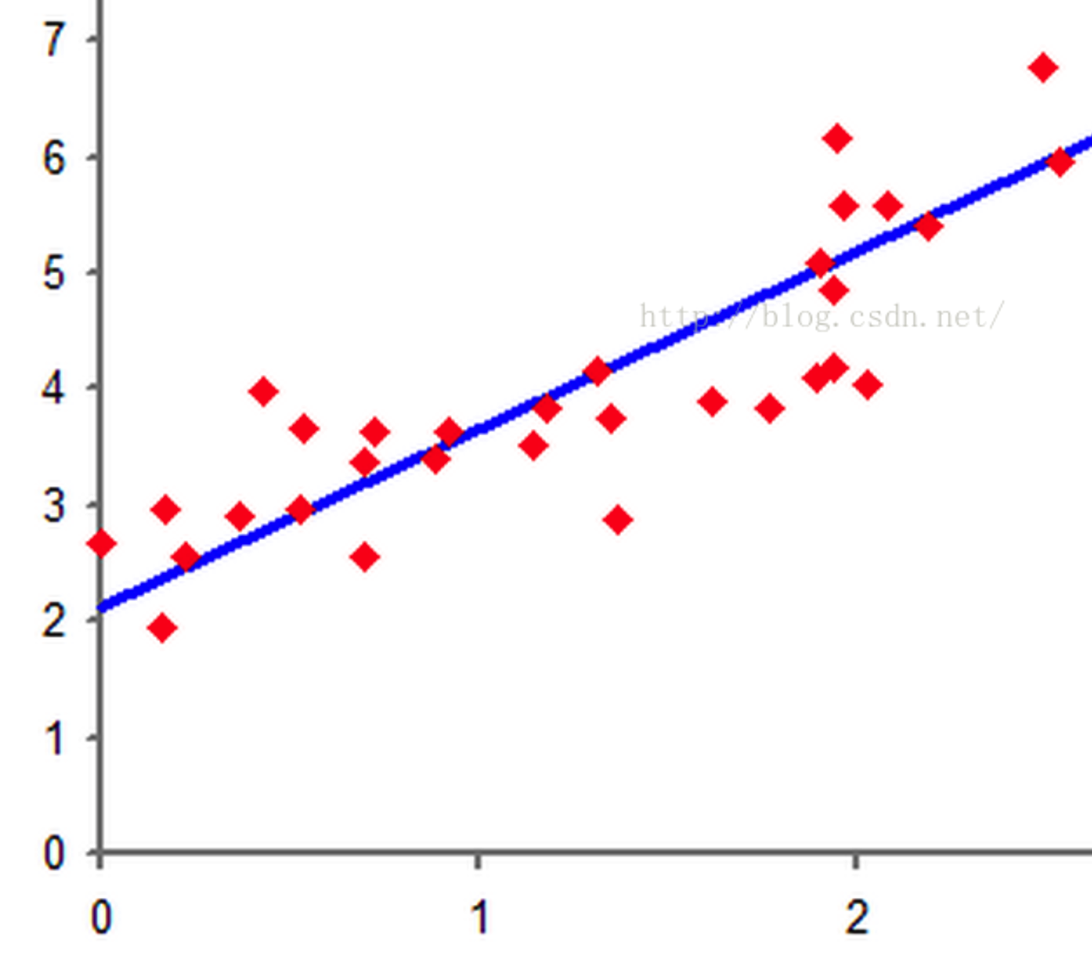
遇到这个问题时，我们首先做的是把数据的特征放到空间中，看有没有什么好的特点。如下，从网上取的图。

这些是二维空间的点，我们想在空间中找到一个超平面，在二维空间中超平面的为一条直线f(x)，当我们带入数据时：

得到这样的结果。其中

就是我们所要求的的直线。那么找这个直线怎么找，在机器学习中，我们要找的是一个学习模型，然后通过损失函数来进行模型参数的求解。那么对于逻辑回归，求逻辑回归的参数就是w和b，那么这个损失函数应该怎么设置。给一条数据，我们希望，他距离这个直线越远我们越可以认为能够很好的进行分类，即属于这个类的可信度就越高。那么我们就需要有一个函数来反应这个情况啊，古人也很聪明啊，使用了logistics函数：

而且这个函数又非常的好，f(x)来衡量数据距离超平面的距离二维中是直线，他被成为函数间隔，f(x)是有正负的，上图中，在直线上面的点发f(x)是负的，相反位于其下的点事正的。这个为什么？是解析几何的最基本的一些性质了。

是直线，而不在这个直线上的点f(x)是带入后，其实是不等于0的，但是有规律，则就可以通过这个规律来进行划分分类。以上面的图为讨论对象，位于上方的点是负的，为与下方的点是正的，那么当f(x)为正，越来越大，则说明点在直线的下方越来越靠下，那么他分为一个类的可能性是不是越大啊，相反，在上方的时候，f(x)是负的，越来越远的时候，是不是越靠近另一个类啊。那么logistics函数不就是反应了这个现象吗？我们类别设置成0或者1，当f(x)正向最大时为1，f(x)负向最大时为0，多好。下面给一下logistics的图像(网上盗图)：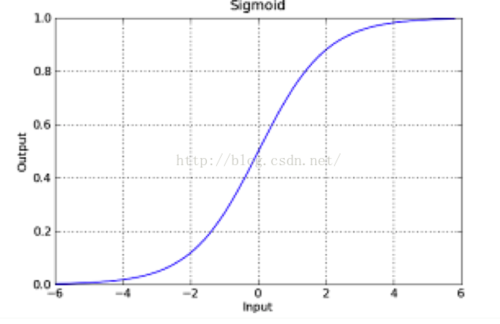

这个函数是不是可以反应出我们所说的情况。其中f(x)就是我们logistics函数的x轴的值。y可以是一个程度，h越大，则说明其分为正类1的可能性越大，h越小，则说明分为负类0可能性越大。那么在数学中可能性的度量是什么？概率啊，logistics函数的大小刚好是[0,1]之间的，多好啊。那么我们以前的求直线问题就转化为求如下的函数:

把以前的问题就转化为求概率的问题

为什么把y放上面，我认为这只是数学上的一种表示形式，给一个特征样本，要么属于0类的，要么属于1类的，在不知道的情况下这样表示和最后知道类别得到的概率是一样的嘛。变化后的logistics函数其中的参数也只是包含w和b，那么我们求解超平面转化为了求解h函数，在概率问题中，求解最优化的损失函数是谁？这又涉及到另外一个问题，我的数学模型已经有了，数学模型中包含一些参数，我需要进行抽样，得到这个问题的一些样本，理由这些样本来对参数进行估计，对参数估计时需要一个损失函数。概率问题最优化的损失函数一般用的是最大似然函数，也就是通过最大似然估计进行计算。这样大家又会问，最大似然估计最大化的是什么？只有知道最大化的是什么的时候，我们才能构造出似然函数啊。刚才我们说了进行参数估计时，我们需要一个样本，那么最大似然函数最大化的是这个样本出现的概率最大，从而来求解参数。可能有点抽象，在样本空间中，样本空间的数据很大，我们想得到含有n个对象的样本，这样含有n个的样本是不是有很多很多，不同的人得到的样本数据也不一样，那么在我们已经得到了这n个样本的情况下，我们进行参数估计，最大似然估计最大化的是我们已经得到的样本在整个样本空间中出现的概率最大，从而来求解参数。

最大似然估计

通过上面的讨论，我们很容易构造出我们的似然函数：

这就很简单了，把上面的似然函数对数化，即：

一般有数学基础的人都会知道我们这个下面就是求导呗，现在的x和y都是已知的只有w是未知的，我们要求的是找到w是我们抽到这个样本的概率最大。但是有一个问题，这样平白无故的求的w不一定是我们这个样本中最优的啊，不是让我们在整个样本空间中进行求导，而是我们有一个样本，在这n个样本中找到我们最想要那个的w，这个用什么啊，这种搜索算法最常用的就是梯度下降啊，沿着梯度的负方向来找我们想要的点。

1、图中的i表示的是第i个记录，j表示的一个记录中的第j个特征分量

2、上面的推导中1→ 2为什么有求和，而后又不存在了啊，这个是和梯度下降法有关系的，梯度下降法就是在当前点下找到一个梯度最大的点作为下一个可以使用的，所有在1到2中，去掉了求和号

3、2→ 3的推导是根据logistics函数的性质得到的。

如果这还是不懂，那没有办法了。

本文出自 “大数据学习” 博客，请务必保留此出处http://9269309.blog.51cto.com/9259309/1875161