矩阵的QR分解(三种方法)
Posted 1357
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵的QR分解(三种方法)相关的知识,希望对你有一定的参考价值。
1.Gram-Schmidt正交化
假设原来的矩阵为[a,b],a,b为线性无关的二维向量,下面我们通过Gram-Schmidt正交化使得矩阵A为标准正交矩阵:
假设正交化后的矩阵为Q=[A,B],我们可以令A=a,那么我们的目的根据AB=I来求B,B可以表示为b向量与b向量在a上的投影的误差向量:
$$B=b-Pb=b-\\frac{A^Tb}{A^TA}A$$

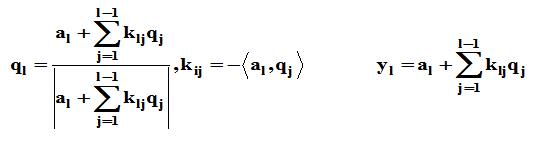
2.Givens矩阵与Givens变换

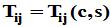 。
。由Givens矩阵所确定的线性变换称为Givens变换(初等旋转变换)。
实数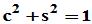 ,故存在
,故存在 ,使
,使 。
。
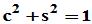 ,故存在
,故存在 ,使
,使 。
。

3.Householder矩阵与Householder变换

平面直角坐标系中,将向量 关于
关于 轴作为交换,则得到
轴作为交换,则得到


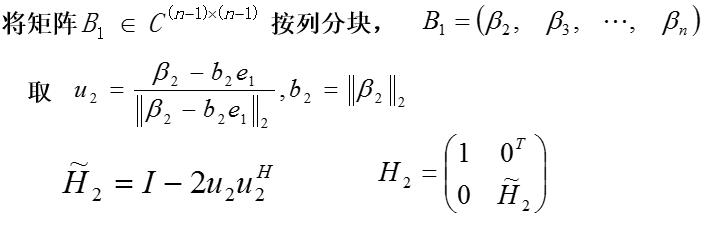

1 #coding:utf8 2 import numpy as np 3 4 def gram_schmidt(A): 5 """Gram-schmidt正交化""" 6 Q=np.zeros_like(A) 7 cnt = 0 8 for a in A.T: 9 u = np.copy(a) 10 for i in range(0, cnt): 11 u -= np.dot(np.dot(Q[:, i].T, a), Q[:, i]) # 减去待求向量在以求向量上的投影 12 e = u / np.linalg.norm(u) # 归一化 13 Q[:, cnt] = e 14 cnt += 1 15 R = np.dot(Q.T, A) 16 return (Q, R) 17 18 def givens_rotation(A): 19 """Givens变换""" 20 (r, c) = np.shape(A) 21 Q = np.identity(r) 22 R = np.copy(A) 23 (rows, cols) = np.tril_indices(r, -1, c) 24 for (row, col) in zip(rows, cols): 25 if R[row, col] != 0: # R[row, col]=0则c=1,s=0,R、Q不变 26 r_ = np.hypot(R[col, col], R[row, col]) # d 27 c = R[col, col]/r_ 28 s = -R[row, col]/r_ 29 G = np.identity(r) 30 G[[col, row], [col, row]] = c 31 G[row, col] = s 32 G[col, row] = -s 33 R = np.dot(G, R) # R=G(n-1,n)*...*G(2n)*...*G(23,1n)*...*G(12)*A 34 Q = np.dot(Q, G.T) # Q=G(n-1,n).T*...*G(2n).T*...*G(23,1n).T*...*G(12).T 35 return (Q, R) 36 37 def householder_reflection(A): 38 """Householder变换""" 39 (r, c) = np.shape(A) 40 Q = np.identity(r) 41 R = np.copy(A) 42 for cnt in range(r - 1): 43 x = R[cnt:, cnt] 44 e = np.zeros_like(x) 45 e[0] = np.linalg.norm(x) 46 u = x - e 47 v = u / np.linalg.norm(u) 48 Q_cnt = np.identity(r) 49 Q_cnt[cnt:, cnt:] -= 2.0 * np.outer(v, v) 50 R = np.dot(Q_cnt, R) # R=H(n-1)*...*H(2)*H(1)*A 51 Q = np.dot(Q, Q_cnt) # Q=H(n-1)*...*H(2)*H(1) H为自逆矩阵 52 return (Q, R) 53 54 np.set_printoptions(precision=4, suppress=True) 55 A = np.array([[6, 5, 0],[5, -1, 4],[5, 1, -14],[0, 4, 3]],dtype=float) 56 57 (Q, R) = gram_schmidt(A) 58 print(Q) 59 print(R) 60 print np.dot(Q,R) 61 62 (Q, R) = givens_rotation(A) 63 print(Q) 64 print(R) 65 print np.dot(Q,R) 66 67 (Q, R) = householder_reflection(A) 68 print(Q) 69 print(R) 70 print np.dot(Q,R)
以上是关于矩阵的QR分解(三种方法)的主要内容,如果未能解决你的问题,请参考以下文章