机器学习算法--svm实战
Posted 坚持不懈--成功
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习算法--svm实战相关的知识,希望对你有一定的参考价值。
1、不平衡数据分类问题
对于非平衡级分类超平面,使用不平衡SVC找出最优分类超平面,基本的思想是,我们先找到一个普通的分类超平面,自动进行校正,求出最优的分类超平面
测试代码如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
rng = np.random.RandomState(0)
n_samples_1 = 1000
n_samples_2 = 100
X = np.r_[1.5 * rng.randn(n_samples_1, 2),0.5 * rng.randn(n_samples_2, 2) + [2, 2]]
y = [0] * (n_samples_1) + [1] * (n_samples_2)
print X
print y
clf = svm.SVC(kernel=\'linear\', C=1.0)
clf.fit(X, y)
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - clf.intercept_[0] / w[1]
wclf = svm.SVC(kernel=\'linear\', class_weight={1: 10})
wclf.fit(X, y)
ww = wclf.coef_[0]
wa = -ww[0] / ww[1]
wyy = wa * xx - wclf.intercept_[0] / ww[1]
h0 = plt.plot(xx, yy, \'k-\', label=\'no weights\')
h1 = plt.plot(xx, wyy, \'k--\', label=\'with weights\')
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.legend()
plt.axis(\'tight\')
plt.show()
运行结果如下:
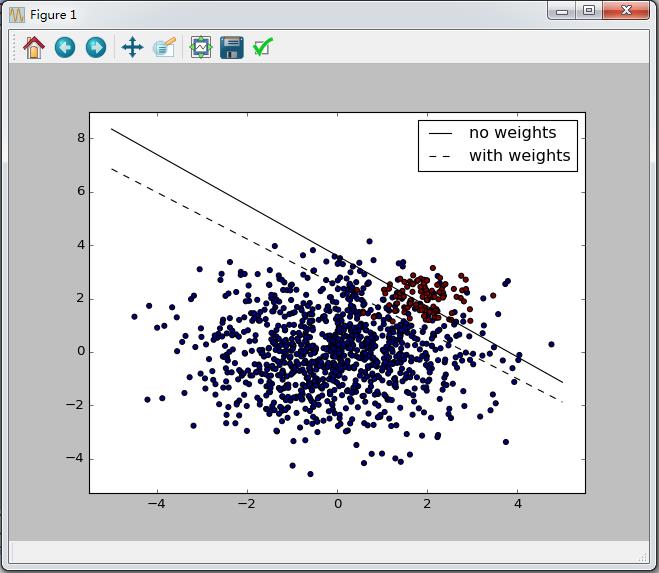
2、回归问题
支持分类的支持向量机可以推广到解决回归问题,这种方法称为支持向量回归
支持向量分类所产生的模型仅仅依赖于训练数据的一个子集,因为构建模型的成本函数不关心在超出边界范围的点,类似的,通过支持向量回归产生的模型依赖于训练数据的一个子集,因为构建模型的函数忽略了靠近预测模型的数据集。
有三种不同的实现方式:支持向量回归SVR,nusvr和linearsvr。linearsvr提供了比SVR更快实施但只考虑线性核函数,而nusvr实现比SVR和linearsvr略有不同。
测试代码
import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as plt
X = np.sort(5 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - np.random.rand(8))
svr_rbf = SVR(kernel=\'rbf\', C=1e3, gamma=0.1)
svr_lin = SVR(kernel=\'linear\', C=1e3)
svr_poly = SVR(kernel=\'poly\', C=1e3, degree=2)
y_rbf = svr_rbf.fit(X, y).predict(X)
y_lin = svr_lin.fit(X, y).predict(X)
y_poly = svr_poly.fit(X, y).predict(X)
lw = 2
plt.scatter(X, y, color=\'darkorange\', label=\'data\')
plt.hold(\'on\')
plt.plot(X, y_rbf, color=\'navy\', lw=lw, label=\'RBF model\')
plt.plot(X, y_lin, color=\'c\', lw=lw, label=\'Linear model\')
plt.plot(X, y_poly, color=\'cornflowerblue\', lw=lw, label=\'Polynomial model\')
plt.xlabel(\'data\')
plt.ylabel(\'target\')
plt.title(\'Support Vector Regression\')
plt.legend()
plt.show()
运行结果如下:
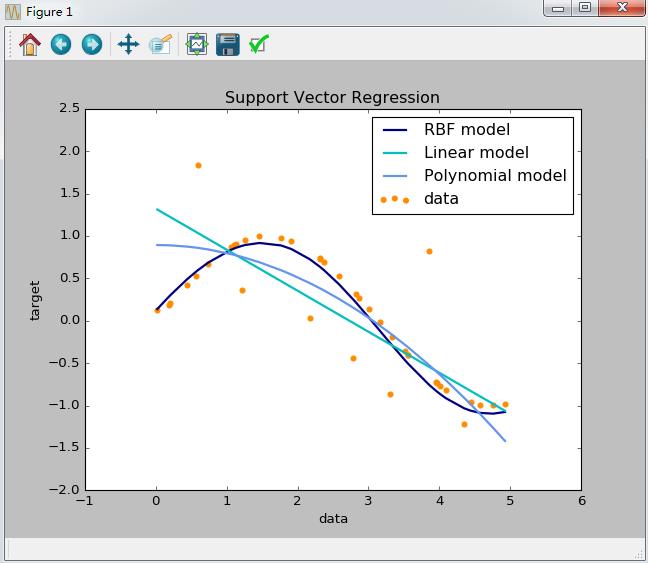
以上是关于机器学习算法--svm实战的主要内容,如果未能解决你的问题,请参考以下文章