朴素贝叶斯

Posted 2020-08-19 曹孟德

    利用近邻方法，很难量化分类的置信度。而基于概率的分类方法--贝叶斯方法，不仅可以分类，还可以给出分类概率。近邻方法别称为惰性学习方法(lazy learner)，当给出数据时，这些分类器只是将他们保存或者记录下来，每次对实例进行训练时，这些分类器都会遍历整个数据集，所以分类器的速度往往跟不上，贝叶斯方法称为勤快学习方法(eager learner).给定训练数据时，这些分类器立即分析数据并构建模型。当要对某个实例进行分类时，他会使用训练得到的内部模型。从而在速度上，勤快学习器优于惰性分类器。

贝叶斯公式：

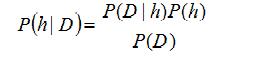
     朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

实例：共和党 VS 民主党，根据两个党派投票记录来预测是哪个党派

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# __author__ : \'小糖果\'

import os
import pprint

class BayesClassfier(object):

    def __init__(self,fp):
        self.acc = 0.0
        self.data = []
        for i in range(1,11):
            with open(os.path.join(fp,\'hv-%02i\'%i),\'r\') as f:
                for line in f:
                    self.data.append(line.split())

        # 开始计数
        self.conditional = {}
        self.prior = {}
        for d in self.data:
            self.prior.setdefault(d[0],0.0)
            self.prior[d[0]] += 1
            self.conditional.setdefault(d[0],{})
            for key in range(16):
                self.conditional[d[0]].setdefault(key,{})
                self.conditional[d[0]][key].setdefault(d[key+1],0.0)
                self.conditional[d[0]][key][d[key+1]] += 1

         # 求先验概率
        tolP = sum(self.prior.values())
        for key in self.prior:
            self.prior[key] /= tolP

        # 求条件概率
        for key1 in self.conditional:
            for key2 in self.conditional[key1]:
                tols = sum(self.conditional[key1][key2].values())
                for key3 in self.conditional[key1][key2]:
                    self.conditional[key1][key2][key3] /= tols

    def predict_classfy(self,d):
        labels = {}
        for label in self.conditional:
            labels.setdefault(label,1.0)
            for key in self.conditional[label]:
                labels[label] *= self.conditional[label][key][d[key]]
            labels[label] *= self.prior[label]

        maxP = max(labels.values())
        for label,p in labels.items():
            if maxP == p:
                return label

    def accurcy(self):
        for d in self.data:
            if d[0] == self.predict_classfy(d[1:]):
                self.acc += 1
        self.acc /= len(self.data)

def test():
    fp = r\'C:\\Users\\TD\\Desktop\\data\\DataMining\\ch6\\house-votes\'
    instances = BayesClassfier(fp)
    instances.accurcy()
    print instances.acc

if __name__ == \'__main__\':
    test()

概率估计问题

      朴素贝叶斯中的概率是真实概率的估计值。当某个事件发生概率很小时，可能在所选取的样本中发生个体为0.这时候基于频率的概率估计就会出现0概率，他会主导贝叶斯的计算过程，不管其它值是什么都无济于事。问题解决办法如下：

 

其中m是一个称为等效的样本容量，有很多中确定m的方法，例如可以设定m为属性的个数，p设定为1/属性个数。这样处理可以避免概率为0带来的影响。

属性问题

   朴素贝叶斯可以运用于非数值属性，也可以用于数值属性，那么上面的例子就是应用于非数值型的。对于贝叶斯方法，我们做的是计数，如果对于一些连续数值的属性，如何使用贝叶斯？方法一可以构建类别，比如讲年龄分为18<,18-22,23-30,30-40,>40等不同档次，这样就将数值信息转换为离散值，就可以像前面一样使用贝叶斯。方法二是使用高斯分布，高斯分布即为正态分布，我们假设了属性值满足高斯分布，然后利用概率，高斯分布的密度函数来计算概率。可用如下公式如下：

  

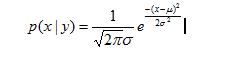
下面是印第安人的糖尿病数据。将实体数据按高斯分布来计算概率，然后使用朴素贝叶斯分类：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# __author__ : \'小糖果\'

import os
import numpy as np
import pprint

class BayesClassfier(object):

    def __init__(self, fp, testBucket):

        self.test = []
        with open(os.path.join(fp,\'pima-%02i\'%testBucket),\'r\') as f:
            for line in f:
                self.test.append(line.split())

        self.prior = {}
        self.numericValues = {}

        # 统计训练样本的信息
        for i in range(1,11):
            if i != testBucket:
                with open(os.path.join(fp, \'pima-%02i\' % i),\'r\') as f:
                    for line in f:
                        d = line.split()
                        self.prior.setdefault(d[-1],0.0)
                        self.prior[d[-1]] += 1
                        self.numericValues.setdefault(d[-1],{})
                        for k in range(8):
                            self.numericValues[d[-1]].setdefault(k,[])
                            self.numericValues[d[-1]][k].append(float(d[k]))
        # 计算先验概率
        tols = sum(self.prior.values())
        for k in self.prior:
            self.prior[k] /= tols

        # 计算中位数和标准差
        self.mean = {}
        self.std = {}
        for k,v in self.numericValues.items():
            self.mean.setdefault(k,{})
            self.std.setdefault(k,{})
            for k1,v1 in v.items():
                self.std[k][k1] = np.std(v1)
                self.mean[k][k1] = np.mean(v1)

    def pdf(self,m,s,x):
        return 1./(np.sqrt(np.pi*2)*s)*np.exp(-((x-m)**2)/(2*(s**2)))

    def get_class(self,d):
        labels = {}
        for label in self.prior:
            labels.setdefault(label,1.0)
            for k in range(8):
                labels[label] *= self.pdf(self.mean[label][k],
                                          self.std[label][k],
                                          float(d[k]))
            labels[label] *= self.prior[label]

        maxP = max(labels.values())
        for k,v in labels.items():
            if maxP == v:
                return k

    def crossVaild(self):
        acc = 0
        for d in self.test:
            if self.get_class(d[:-1]) == d[-1]:
                acc += 1
        return acc*1./len(self.test)


def test():
    fp = r\'C:\\Users\\TD\\Desktop\\data\\DataMining\\ch6\\pima\'
    acc = 0.0
    for testBucket in range(1,11):
        instance = BayesClassfier(fp,testBucket)
        acc += instance.crossVaild()
    acc /= 10
    print acc
if __name__ ==\'__main__\':
    test()

正确率77.33%

贝叶斯于Knn的比较：

贝叶斯的优点： 

     1 实现简单，只是简单的计数问题

     2 和其他方法比，需要训练的数据少

贝叶斯主要确点：贝叶斯不能学习到特征的相互联系。

Knn主要优点：

     1 实现简单

     2 不用假设数据具有特定的结构

Knn 主要缺点： 需要大量的内存来存取数据

朴素贝叶斯中“朴素”的含义：贝叶斯的的工作有效需要特征间相互独立，但是大部分实际问题都不满足这一条件，我们只是假设他们间相互独立，之所以叫做朴素贝叶斯是因为我们知道知道特征间可能存在不独立，但是我们仍然假设他们独立。事实说明，尽管朴素的假设存在，贝叶斯的效果依然不错。