arima模型python 怎么看平稳性
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了arima模型python 怎么看平稳性相关的知识,希望对你有一定的参考价值。
时间序列分析(一) 如何判断序列是否平稳序列平稳不平稳,一般采用两种方法:
第一种:看图法
图是指时序图,例如(eviews画滴):
分析:什么样的图不平稳,先说下什么是平稳,平稳就是围绕着一个常数上下波动。
看看上面这个图,很明显的增长趋势,不平稳。
第二种:自相关系数和偏相关系数
还以上面的序列为例:用eviews得到自相关和偏相关图,Q统计量和伴随概率。
分析:判断平稳与否的话,用自相关图和偏相关图就可以了。
平稳的序列的自相关图和偏相关图不是拖尾就是截尾。截尾就是在某阶之后,系数都为 0 ,怎么理解呢,看上面偏相关的图,当阶数为 1 的时候,系数值还是很大, 0.914. 二阶长的时候突然就变成了 0.050. 后面的值都很小,认为是趋于 0 ,这种状况就是截尾。再就是拖尾,拖尾就是有一个衰减的趋势,但是不都为 0 。
自相关图既不是拖尾也不是截尾。以上的图的自相关是一个三角对称的形式,这种趋势是单调趋势的典型图形。
下面是通过自相关的其他功能
如果自相关是拖尾,偏相关截尾,则用 AR 算法
如果自相关截尾,偏相关拖尾,则用 MA 算法
如果自相关和偏相关都是拖尾,则用 ARMA 算法, ARIMA 是 ARMA 算法的扩展版,用法类似 。
不平稳,怎么办?
答案是差分
还是上面那个序列,两种方法都证明他是不靠谱的,不平稳的。确定不平稳后,依次进行1阶、2阶、3阶...差分,直到平稳位置。先来个一阶差分,上图。
从图上看,一阶差分的效果不错,看着是平稳的。 参考技术A
原文链接:http://tecdat.cn/?p=20742
时间序列 被定义为一系列按时间顺序索引的数据点。时间顺序可以是每天,每月或每年。
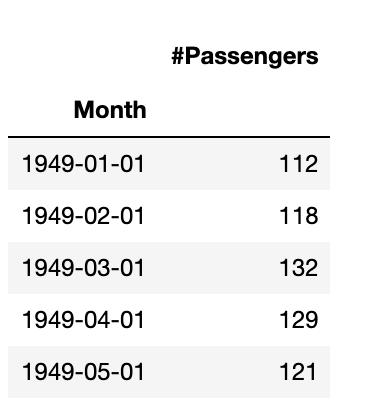
以下是一个时间序列示例,该示例说明了从1949年到1960年每月航空公司的乘客数量。
时间序列预测
时间序列预测是使用统计模型根据过去的结果预测时间序列的未来值的过程。
一些示例
预测未来的客户数量。
解释销售中的季节性模式。
检测异常事件并估计其影响的程度。
估计新推出的产品对已售出产品数量的影响。
时间序列的组成部分:
代码:航空公司乘客的ETS分解数据集:
# 导入所需的库import numpy as np# 读取AirPassengers数据集airline = pd.read_csv('data.csv', index_col ='Month', parse_dates = True)# 输出数据集的前五行airline.head()# ETS分解# ETS图result.plot()输出:
请点击输入图片描述

请点击输入图片描述
ARIMA时间序列预测模型
ARIMA代表自回归移动平均模型,由三个阶数参数 (p,d,q)指定。
ARIMA模型的类型
自动ARIMA
“ auto_arima” 函数 可帮助我们确定ARIMA模型的最佳参数,并返回拟合的ARIMA模型。
代码:ARIMA模型的参数分析
# 忽略警告import warningswarnings.filterwarnings("ignore")# 将自动arima函数拟合到AirPassengers数据集autoarima(airline['# Passengers'], start_p = 1, start_q = 1, max_p = 3, max_q = 3, m = 12, stepwise = True # 设置为逐步# 输出摘要stepwise_fit.summary()输出:
请点击输入图片描述
代码:将ARIMA模型拟合到AirPassengers数据集
# 将数据拆分为训练/测试集test = iloc[len(airline)-12:] # 设置一年(12个月)进行测试# 在训练集上拟合一个SARIMAX(0,1,1)x(2,1,1,12)SARIMAX(Passengers, order = (0, 1, 1), seasonal_order =(2, 1, 1, 12result.summary()输出: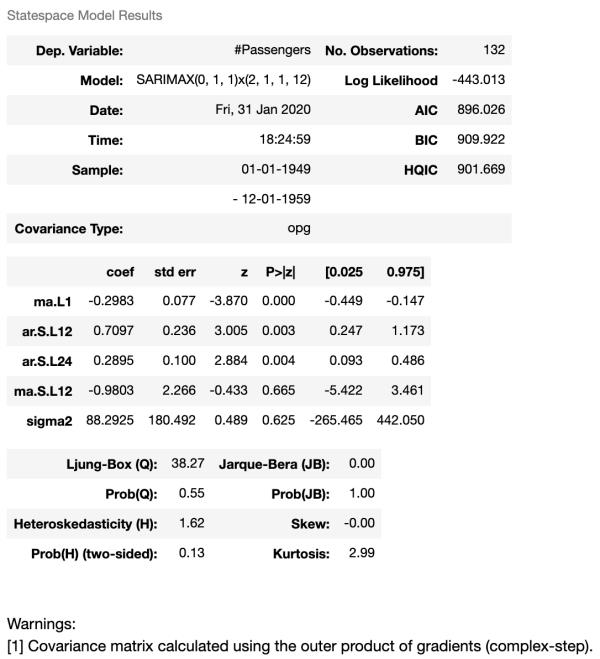
请点击输入图片描述
代码:ARIMA模型对测试集的预测
# 针对测试集的一年预测predict(start, end,#绘图预测和实际值predictions.plot输出:
请点击输入图片描述
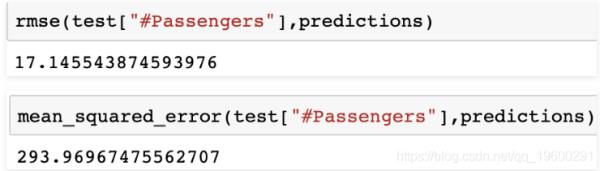
代码:使用MSE和RMSE评估模型
# 加载特定的评估工具# 计算均方根误差rmse(test["# Passengers"], predictions)# 计算均方误差mean_squared_error(test["# Passengers"], predictions)输出:
请点击输入图片描述

请点击输入图片描述
代码:使用ARIMA模型进行预测
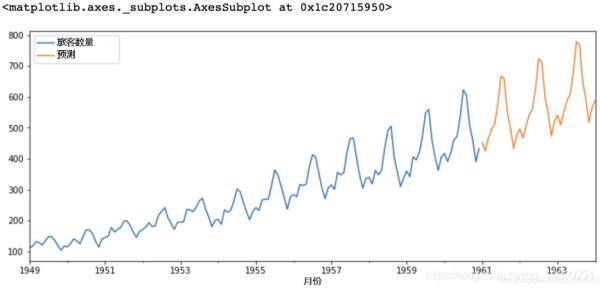
# 在完整数据集上训练模型result = model.fit()# 未来3年预测result.predict(start = len(airline), end = (len(airline)-1) + 3 * 12, # 绘制预测值forecast.plot(legend = True)输出:
请点击输入图片描述
趋势:趋势显示了长时间序列数据的总体方向。趋势可以是增加(向上),减少(向下)或水平(平稳)。
季节性:季节性成分在时间,方向和幅度方面表现出重复的趋势。一些例子包括由于炎热的天气导致夏季用水量增加,或每年假期期间航空公司乘客人数增加。
周期性成分: 这些是在特定时间段内没有稳定重复的趋势。周期是指时间序列的起伏,通常在商业周期中观察到。这些周期没有季节性变化,但通常会在3到12年的时间范围内发生,具体取决于时间序列的性质。
不规则变化: 这些是时间序列数据中的波动,当趋势和周期性变化被删除时,这些波动变得明显。这些变化是不可预测的,不稳定的,并且可能是随机的,也可能不是随机的。
ETS分解
ETS分解用于分解时间序列的不同部分。ETS一词代表误差、趋势和季节性。
AR(p)自回归 –一种回归模型,利用当前观测值与上一个期间的观测值之间的依存关系。自回归(AR(p))分量是指在时间序列的回归方程中使用过去的值。
I(d) –使用观测值的差分(从上一时间步长的观测值中减去观测值)使时间序列稳定。差分涉及将序列的当前值与其先前的值相减d次。
MA(q)移动平均值 –一种模型,该模型使用观测值与应用于滞后观测值的移动平均值模型中的残留误差之间的相关性。移动平均成分将模型的误差描述为先前误差项的组合。 q 表示要包含在模型中的项数。
ARIMA:非季节性自回归移动平均模型
SARIMA:季节性ARIMA
SARIMAX:具有外生变量的季节性ARIMA

请点击输入图片描述
最受欢迎的见解
1.在python中使用lstm和pytorch进行时间序列预测
2.python中利用长短期记忆模型lstm进行时间序列预测分析
3.使用r语言进行时间序列(arima,指数平滑)分析
4.r语言多元copula-garch-模型时间序列预测
5.r语言copulas和金融时间序列案例
6.使用r语言随机波动模型sv处理时间序列中的随机波动
7.r语言时间序列tar阈值自回归模型
8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类
9.python3用arima模型进行时间序列预测
算法 | 时间序列: 从平稳到非平稳ARIMA 模型
先看下图:
这是1986年到2006年的原油月度价格。可见在2001年之后,原油价格有一个显著的攀爬。这时再去假定均值是一个定值(常数)就不太合理了,也就是说,第二讲里提到的ARMA平稳模型在这种情况下就太适用了。也因此有了今天这一文。
要处理这种非平稳的数据(比如上图中的均值不是一个常数),需要用非平稳模型:求和自回归滑动平均(Autoregressive integrated moving average, ARIMA)。接下来,咱先看一个处理过的石油价格:
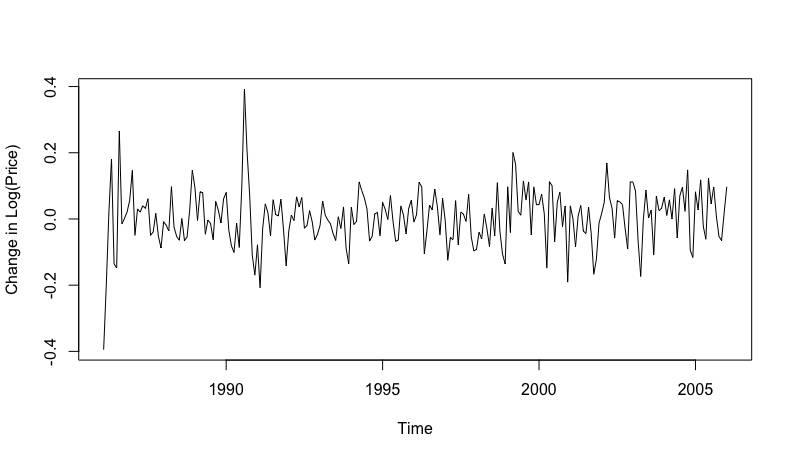
是不是似曾相识?! 对的,经过简单的处理,本来不平稳的数据,立即变成了平稳数据了。这样再用上一章的模型就可简单处理了。这种处理方式就叫做差分(马上会讲,别急)。 而ARIMA 模型可以简单的理解为:差分+平稳模型。你看,这下,这章的内容是不是简单多了,所谓非平稳模型不就是差分处理下数据,再变有平稳数据,然后再用平稳模型处理嘛~ 确实酱紫~。
那马上就产生一个问题(或者你早就有疑问了):什么叫做差分?差分是处理时间序列非常重要的工具,在计量经济学及金融数学中广泛应用。
3.1 差分运算
3.1.1 差分运算
还是用原油价格(月度数据)作为例子,所谓一阶差分就是两个相邻月度之间做差。(这么简单?!对,就是这样~)。
规范化些:设
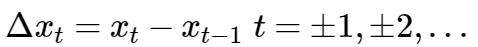
称为时间序列
比如 2005年原油价格为:46.84 ,48.15, 54.19, 52.98, 49.83, 56.35, 58.99, 64.98 ,65.59, 62.26, 58.32 ,59.41。那这组数据的一阶差分即为 1.31, 6.04, -1.21, -3.15, 6.52 , 2.64 , 5.99 , 0.61,-3.33, -3.94,也就是前一个数减去后一个数而已。
那如果我想去差分后的数据再做一次差分呢? 那就是二阶差分(就是这么easy~):上面的一阶差分数据为1.31, 6.04, -1.21, -3.15, 6.52 , 2.64 , 5.99 , 0.61,-3.33, -3.94,再经一次差分: 4.73 , -7.25, -1.94, 9.67, -3.88, 3.35 , -5.38 , -3.94, -0.61。
那如果想做p次呢(你够了~),那就叫做p阶差分了,定义为:
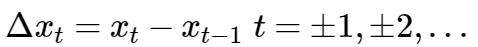
是不是很简单?!
3.1.2 k步差分
如果不是相邻数据间做差呢,比如我想隔几个数据比较,比如我想用原油数据7月份数据与1月份做差呢? 没问题,你的需求我一定满足,这个就叫做k步差分了:
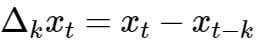
比如2005年7月与1月的价格差值即为: 58.99 - 46.84 = 12.15.也即称为六步差分了。
3.1.3 差分的选择
划重点,划重点!!!
序列蕴含着显著的线性趋势,1 阶差分可以实现趋势平稳,比如上面的原油价格(不过,里面其实做了一个预处理,一会说~).
序列蕴含着曲线趋势的,通常低阶(2阶或3阶)差分就可以取提出曲线趋势的影响.
对于固定周期的序列,通常进行步长为周期长度的差分就可以较好的提取周期信息.
PS: 差分虽好,但也不要贪杯哦, 记住对信息的任何的加工都只会造成信息的损失.
3.1.3* 延迟算子
这一小节作为了解,不喜欢可以_跳过_,不影响理解滴~。
延迟算子,类似一个时间指针,当前序列值乘以一个延迟算子,就相当于把当前序列值的时间向过去拔了一个时刻。(ps: 算子就是映射,就是关系,就是变换[3])
3.1.3.1定义与性质
记 B 为延迟算子,有:
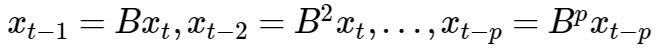
延迟算子具有如下性质:
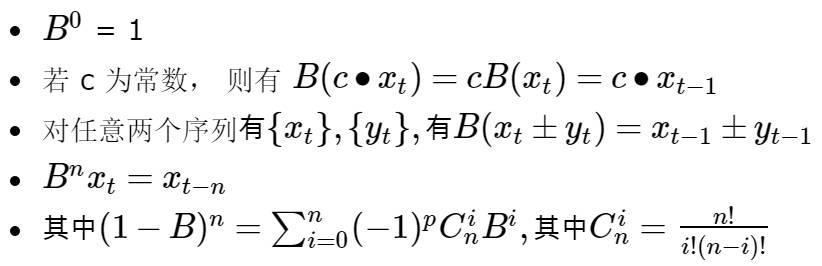
3.1.3.2 差分的延迟算子表示
p阶差分
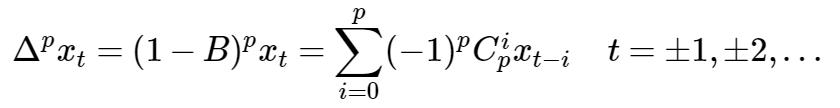
k步差分
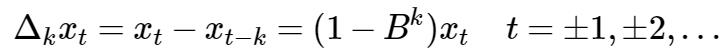
3.2* 时间序列分解
这一小节作为了解,不喜欢可以_跳过_,不影响理解滴~
在第一节(时间序列介绍) 中,曾提到过时间序列分解,其实时间序列分解不是靠感觉给出的,它也是有强大理论依据的,这里就支持时间序列分解的两大定理作简单的介绍:
3.2.1 Wold 分解
Wold 分解: 对于任何一个离散平稳过程{
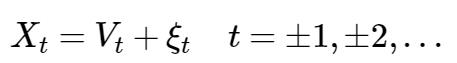
其中
{Vt} 为确定性序列,而
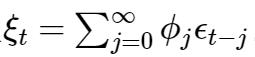 满足:
满足:
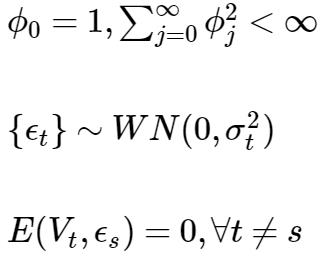
其中的所谓的'确定性':
对任意的序列
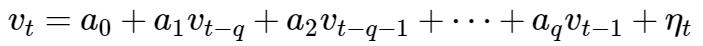
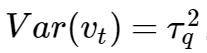
如果:
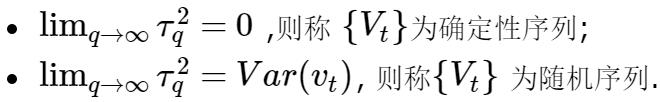
3.2.2 Cramer 分解
Wold分解是现代时间序列分析理论的灵魂。1938 年 H. Wold 提出此理论时,只是为了分析平稳序列的构成, 不过另一位大牛Cramer于1961年证明此种分析思路同样适用于非平稳序列。
Crammer 分解:
任意时间序列
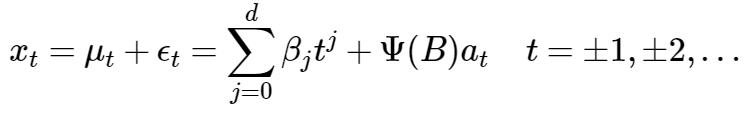
Cramer分解说明任何一具序列的波动都可以视为受到了确定性影响和随机性影响的综合作用.
3.3 ARIMA 模型
千呼万唤终于到了ARIMA.
有了上面的知识,就可以很容易推出自回归滑动平均求和(ARIMA)模型。
如果有一个时间序列
其中 d 通常为1,最多也不过2,3, 所以,不用太担心模型过于复杂。另外,如果 p = 0, 即不包含自回归项, 称为IMA(d,q), 如果没有滑动平均项, 则称为ARI(p,d)。
来来,给个'粟子',先看个简单的,下图(上)是某个商店某产品的两个月销量的时间序列图:
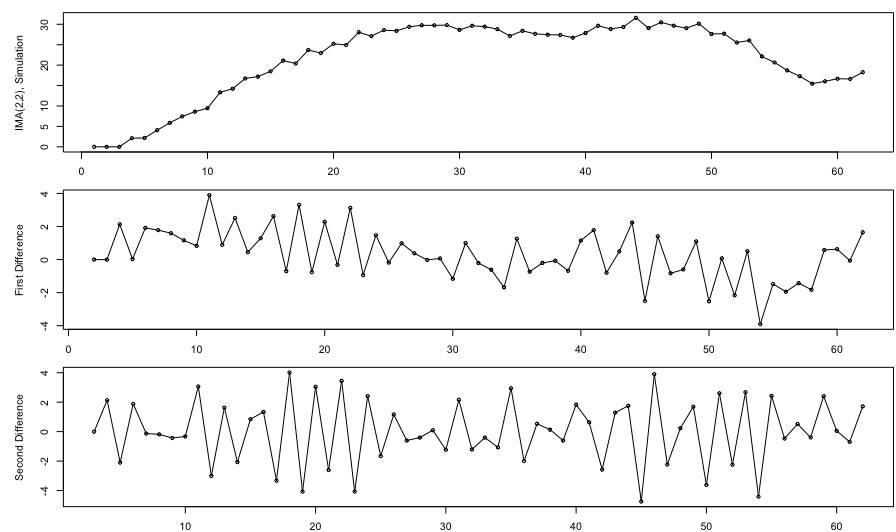
(上)图中,数据显然是不平稳的; (中)图是作了一步差分的结果,是不是平稳多了(什么?图怎么更难看了? 是的, 因为我这个过程是在剔除确定性信息啊~); (下)图是再一次作一步差分的(也即二阶差分), 你会发现这会是真的像白噪声了。
下面考虑ARIMA(p,1,d), 令 Wt=Yt-Yt-1
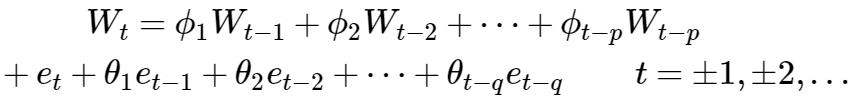
即:
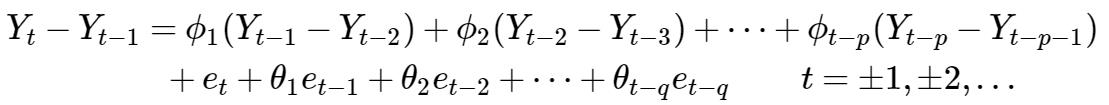
整理:
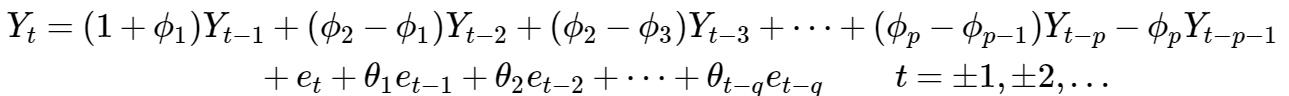
上式即称为模型的差分方程形式, 看起来是不是像ARMA(p+1,q)过程? 不过, 其特征多项式(涉及延迟算子,不过只需要知道下面的公式是由上面推出即可,至于怎么推出,需了解上面的星号章节~[^4])满足:
显然,x = 1 是 一个根, 意味着这个过程非平稳,而其余的根是平稳过程的
参考文献
如第一节参考文献中所述, 主要的参考文献都在第一节中列出来了, 下面所列为新加入或当节的参考文献,请知悉.
1: 王燕 编著, 应用时间序列分析 北京: 中国人民大学出版社,2005
2: http://blog.sina.com.cn/s/blog_a1a5c41501012w3b.html
3: https://wenku.baidu.com/view/aab18a65cfc789eb162dc805.html
夏洛克 ITOA
为企业量身定制的IT运维专家
人工智能 | 机器学习 | IT运维
以上是关于arima模型python 怎么看平稳性的主要内容,如果未能解决你的问题,请参考以下文章