从汉诺塔问题来看“递归”本质
Posted 写代码是一种艺术,甚于蒙娜丽莎的微笑!
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从汉诺塔问题来看“递归”本质相关的知识,希望对你有一定的参考价值。
汉诺塔问题
大二上数据结构课,老师在讲解“栈与递归的实现”时,引入了汉诺塔的问题,使用递归来解决n个盘在(x,y,z)轴上移动。
例如下面的动图(图片出自于汉诺塔算法详解之C++):
三个盘的情况:

四个盘的情况:

如果是5个、6个、7个、...,该如何移动呢?
于是,老师给了一段经典的递归代码:
void hanoi(int n,char x,char y,char z){ if(n == 1) move(x,1,z); else{ hanoi(n-1,x,z,y); move(x,n,z); hanoi(n-1,y,x,z); } }
简简单单的几句代码里蕴含中深奥的秘密啊!
用图像来讲解一下这里面的原理吧,例如下图:
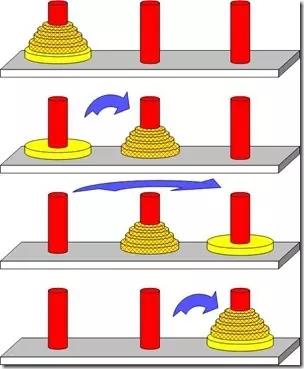
(图片来源于“码农翻身”公众号)
假设盘的序号从上往下增大,第一个盘序号为1,最后一个盘序号为n。每次只能移动一个盘,并且大盘不能在小盘的上面。那么运用递归的思想可知,若想将n号盘放到z轴上,那么必须先将(1,...,n-1)号盘移动到y轴上,此时z轴作为辅助轴。即
hanoi(n-1,x,z,y);
然后移动n号盘到z轴上,即
move(x,n,z);
最后将y轴上的(1,...,n-1)号盘移动到z轴上,此时x轴作为辅助轴。即
hanoi(n-1,y,x,z);
n的阶乘问题
再说一个例子:计算n的阶乘
f(n) = n!
其递归算法如下:
int factorial(int n){ if(n == 1) return 1; else return n * factorial(n-1); }
这段程序加载到内存的分配图如下:

(图片来源于“码农翻身”公众号)
由于递归是函数自身调用自身,所以程序被编译后代码段中只有一份代码。
递归调用是如何进行的呢?
注意看堆栈中的栈帧啊, 每个栈帧就代表了被调用中的一个函数, 这些函数栈帧以先进后出的方式排列起来,就形成了一个栈, 栈帧的结构如下图所示:

(图片来源于“码农翻身”公众号)
相信大家还记得《数据结构》(严蔚敏版)一书中提到的“工作记录”就是指函数栈帧。栈顶指针被称为“当前环境指针”。
忽略到其他内容, 只关注输入参数和返回值的话,阶乘函数factorial(4)的工作栈如下图所示:
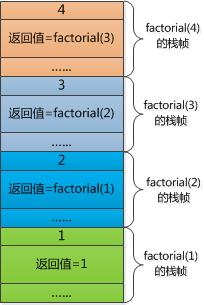
(图片来源于“码农翻身”公众号)
其计算过程如下图所示:
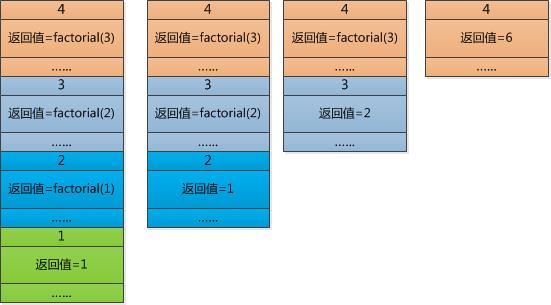
(图片来源于“码农翻身”公众号)
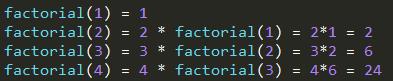
注意, 每个递归函数必须得有个终止条件, 要不然就会发生无限递归了, 永远都出不来了。
当然针对于此递归算法,对于n的值是有限制的。因为堆栈容量是有限的,如果n值太大程序会崩掉。
该如何解决呢?
从上面的代码中可以知道“factorial(n) = n * factorial(n-1 ) ” ,这个计算式是整个程序的核心。 图中每个栈帧都需要记录下当前的n的值, 还要记录下一个函数栈帧的返回值, 然后才能运算出当前栈帧的结果。 也就是说使用多个栈帧是不可避免的。
可以使用下面的递归算法:
int factorial(int n,int result){ if(n == 1){ return result; } else{ return factorial(n-1,n * result); } }
注意函数的最后一个语句, 就不是 n * factorial(n-1) 了, 而是直接调用factorial(....) 这个函数本身, 这就带来了巨大的好处。
计算过程如下:
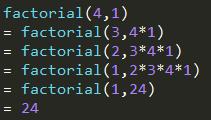
当执行到factorial(1, 24)的时候直接就可以返回结果了。
这就是妙处所在了,计算机发现这种情况,只用一个栈帧就可以搞定这些计算,无论n有多大。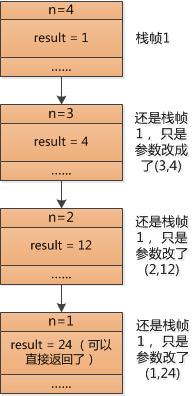
(图片来源于“码农翻身”公众号)
这就是所谓的“尾递归”了, 当递归调用是函数体中最后执行的语句并且它的返回值不属于表达式一部分时, 这个递归就是尾递归。
现代的编译器就会发现这个特点, 生成优化的代码, 复用栈帧。 第一个算法中因为有个n * factorial(n-1) , 虽然也是递归,但是递归的结果处于一个表达式中,还要做计算, 所以就没法复用栈帧了,只能一层一层的调用下去。
另外,向大家推荐一个公众号“码农翻身”。上面有很多有关计算机方面的文章,浅显易懂,十分受用。本文也在一定程度上,吸收了该公众号上的精华。
“码农翻身” 公共号 : 由工作15年的前IBM架构师创建,分享编程和职场的经验教训。

以上是关于从汉诺塔问题来看“递归”本质的主要内容,如果未能解决你的问题,请参考以下文章