258.Add Digits

Posted 2020-06-14

Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.

For example:

Given num = 38, the process is like: 3 + 8 = 11, 1 + 1 = 2. Since 2 has only one digit, return it.

Follow up:
Could you do it without any loop/recursion in O(1) runtime?

 

思路：如果不对复杂度有要求，通过常规算法，不断对10求余和除10，一步一步用for循环相加就能得出结果。但题目中要求不用循环，看了几个hint后，感觉有规律，但仍无法找出具体公式，后来看了wiki百科中的公式后，发现就是1-9不断的循环，问题变得很简单，加起来的数可以归结为一个公式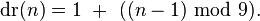，之后的代码就很简单了。

我的代码：

class Solution {
public:
    int addDigits(int num) 
    {
        int s = 1 + (num-1)%9;
        return s;
    }
};

 

参考代码：

class Solution {
    public:

        int addDigits(int num) {
            switch(random()%5+1){
                case 1: return addDigits01(num);
                case 2: return addDigits02(num);
                case 3: return addDigits03(num);
                case 4: return addDigits04(num);
                default: return addDigits05(num);
            }

        }

        //regualr way
        int addDigits01(int num) {
            while(num > 9) {
                int sum;
                for(sum=0; num > 0; sum += num%10 , num/=10);
                num = sum;
            }
            return num;

        }

        //This solution looks is very tricky, but acutally it is easy to understand.
        //it just keep adding the last digital until the num < 10
        int addDigits02(int num) {
            while(num > 9) {
                num = num / 10 + num % 10;
            }
            return num;

        }

        // Let‘s observe the pattern
        //    1    1
        //    2    2
        //    ... ...
        //    8    8    
        //    9    9    
        //    10    1
        //    11    2
        //    12    3    
        //    ... ...
        //    17    8
        //    18    9
        //    19    1
        //    20    2
        //    ...  ...
        // It looks most of number just simply %9 is the answer, 
        // but there are some edge cases.
        //    9%9=0 but we need 9. 
        //    18%9=0 but we need 9
        // so we can find the solution is:
        //    1) num <=9, return num
        //    2) num > 9, reutrn num%9 if num%9>0
        //                return 9 if num%9 ==0
        int addDigits03(int num) {
            return num >9 ? ((num %9)==0 ? 9:num%9) : num;
        }

        //But actually, we can use (num-1)%9 + 1 to make all cases right.
        int addDigits04(int num){
            return (num - 1) % 9 + 1;
        }

        //This solution is similar with pervious solution.
        int addDigits05(int num){
            return num - 9 * ((num - 1)/9);
        }

};

 

总结：参考代码完整得展现了从常规算法，到最简算法的历程，在两三个条件判断下，学习参考代码中的写法：

return num >9 ? ((num %9)==0 ? 9:num%9) : num;
而对同一问题有多种算法时，用switch＋random（）的组合非常好玩，哈哈：

 switch(random()%5+1)