计算几何及其应用——计算几何基础
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了计算几何及其应用——计算几何基础相关的知识,希望对你有一定的参考价值。
写在前面:当时开计算几何这个专题神奇的从解析几何开始了,然后最近发现《计算几何及应用(金博)》这本书前面那章忽略掉了一些重要的东西比如说点定位、半平面相交之类的东西,恰好还有一些和计算几何扯上边但是不需要算法的简单题目没有整理,故在此开辟一块小空间。
我们再来看一道有关几何的问题。(Problem source:hdu2073)
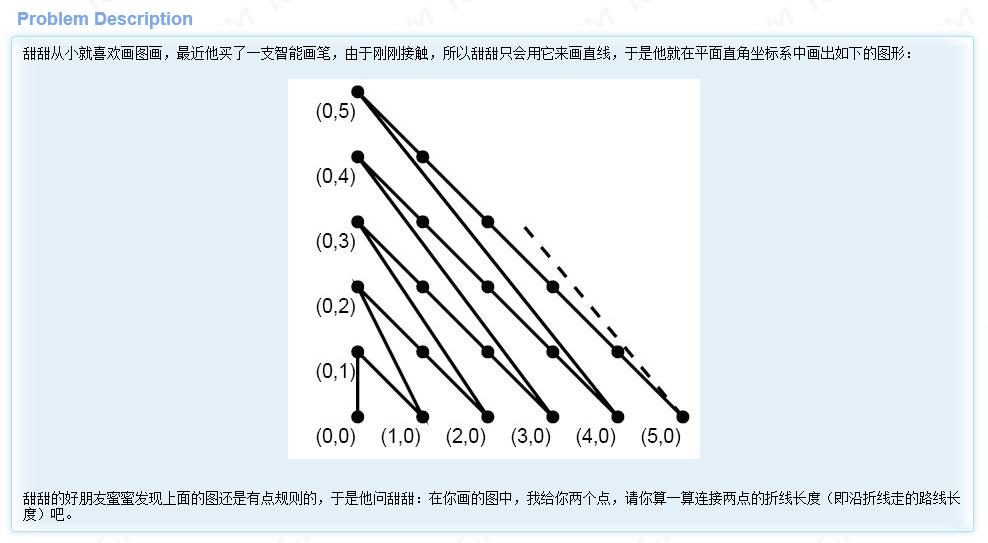
数理分析:虽然这道题异常的简单,基本算不上计算几何这个专题当中的题目,但是把它拿到这里来,是源于这道简单几何题的思路其实体现了计算几何整个体系中比较重要的思维。
这里给出两个点的坐标,我们其实只需找到这两个点到原点的距离,然后相减,便可以得到这两个点的距离。
那么我们如何得到某个点到原点的距离呢?不妨看看某个点到原点的折线呈现出怎样有规律的走向。
①一类是等腰直角三角形的斜边,考虑到这些点其实都在直线x + y = s的直线上,由此我们可以得到这类线段长的总和——s*(s - 1)*sqrt(2) / 2.
②还有一类线段尝试非等腰直角三角形的斜边,可以明显的看出,这些斜边是一系列直角边为i和i - 1的斜边。
③最后一段长度,便是相对于x + y = s这条直线上的不同点。可以说,只要是在这条直线上的点,前面的一段折线距离相等的,只需再加上输入点在该直线上多出的那一段距离,便是总距离。
从以上的数理分析不难发现,计算几何的问题中,对于几何图形的规律化的分类非常重要,这将为设计程序实现自动化编程奠定重要的基础,这一点在凸包问题其实就有所体现。
有了这一层的数理分析,编程实现在几何类的问题不是困难的事情,此处要注意sqrt函数的精度问题。
AC代码如下:
#include<stdio.h> #include<math.h> double dis(int x , int y) { double s = x + y; double distance = s * (s - 1) * sqrt(2.0) * 0.5; for(int i = s;i > 0;i--) distance += sqrt(i * i * 1.0 + (i - 1)*(i - 1)); distance += sqrt(2.0) * x; return distance; } int main() { int x1 , y1 , x2 , y2; int t; scanf("%d",&t); while(t--) { scanf("%d%d%d%d",&x1 , &y1 , &x2 , &y2); printf("%.3lf\n",fabs(dis(x1 , y1) - dis(x2 , y2))); } }
再来看一道有关叉积(在笔者的《计算几何及应用——解析几何》这篇文章有关于叉积定义的引出以及相关规律的证明,这不再累述)应用的简单题目。(Problem scoure:hdu2108)

这道题目是逆时针给出一个n边形的n个顶点,然我们判断它的凹凸性。经过上面关于利用叉积判断三个点的相对位置,这里的数理分析就不是难点了。 关于叉积判断三个点的相对位置的结论如下。
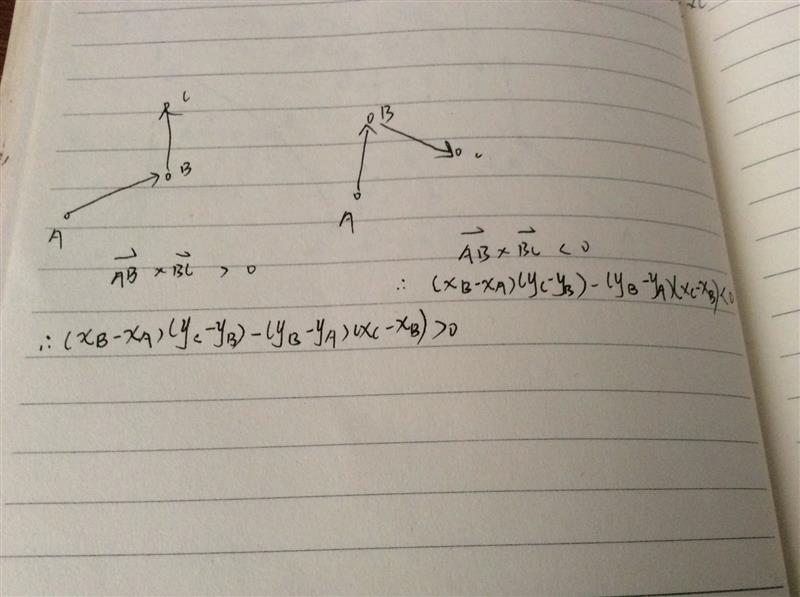
编程实现上,只需遍历的临近的三个点的所有情况,即可。
AC代码如下:
#include<stdio.h> using namespace std; struct point { int x , y; }p[1000]; int Cross_Product(point a , point b , point c) { return (b.x - a.x)*(c.y - b.y) - (b.y - a.y)*(c.x - b.x); } int main() { int n , i; while(scanf("%d",&n) != EOF && n) { for(i = 1;i <= n;i++) scanf("%d %d", &p[i].x , &p[i].y); p[n + 1] = p[1] , p[n + 2] = p[2]; for(i = 3;i <= n + 2;i++) if(Cross_Product(p[i - 2] , p[i - 1] , p[i]) < 0) break; if(i == n + 3) printf("convex\n"); else printf("concave\n"); } return 0; }
我们再看一道关于点定位的题目。(Problem source:hdu 1756)
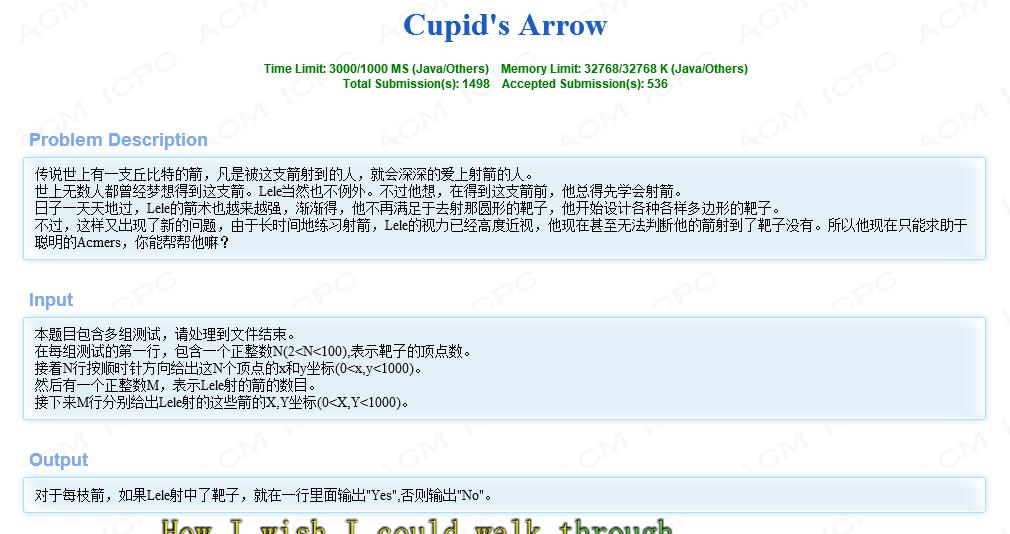
题目大意:就是给出n多边形的n个顶点,然后继续输入点坐标,判断此点是否在这个n多边形内部。
数理分析:这是一个很简化的点定位问题,关于点定位问题有多重解法,包括扫描法、叉乘判断法、角度和判断法。这里我们以扫描法为例进行分析,剩下的方法以后将会介绍。
显然n多边形将整个平面分成了三部分:n边形的里面、上面、外面。而我们要判断某个点是否在这个多边形内部,假设我们任意地做了一条以该点为端点的射线,射线无线延伸最终一定是在n多边形的外边,而这条射线在延伸的过程中,与n多边形有一个交点,就意味着这条射线上的点从图形的内部过渡到了图形的外部或者从图形的外部过渡到了图形的内部,那么我们知道,射线上的点最终的归宿是图形的外面,那么过程中如何产生了1个交点,是否意味着起始点位于图形的内部呢?3、5、7个交点是否意味着相同的含义呢。而交点为2、4、6的时候是否恰好相反呢?概括起来,我们得到一个结论:以某点为端点任意做出的射线,如果和n多边形有偶数个交点,那么这个点在n多边形的外面,如果和n多边形有奇数个交点,那么这个点在n多边形的内部。当然,还有一种情况不能少,那便是这个点在n多边形上。
而仅仅知道了这个还是不够的。在实际作图中会出现下面一些特殊的情况。
(1)射线过了某个顶点;(2)射线经过了某个顶点,却没穿过;(3)射线和某个边重合。
那么现在顾及了以上几种特殊情况,我们还要一般情况下的表达式,即解决这样一个问题:如何判断一条射线与一条线段相交?我们不妨画出各种情况。
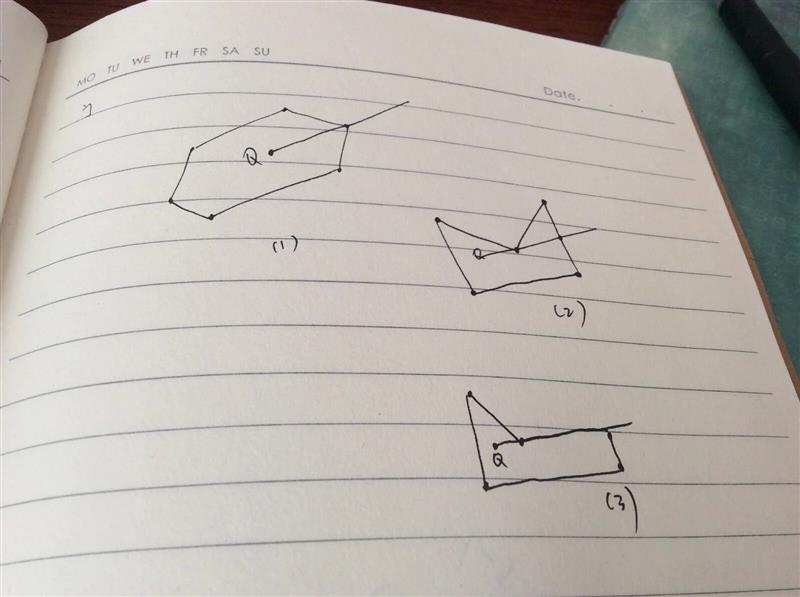
显然(2)是符合要求的情况,那么我们在详细的分析(2)。
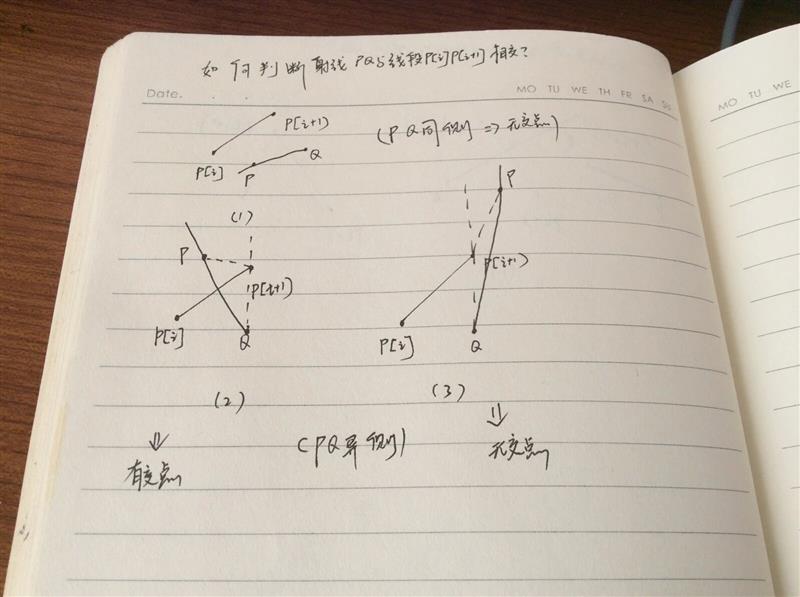
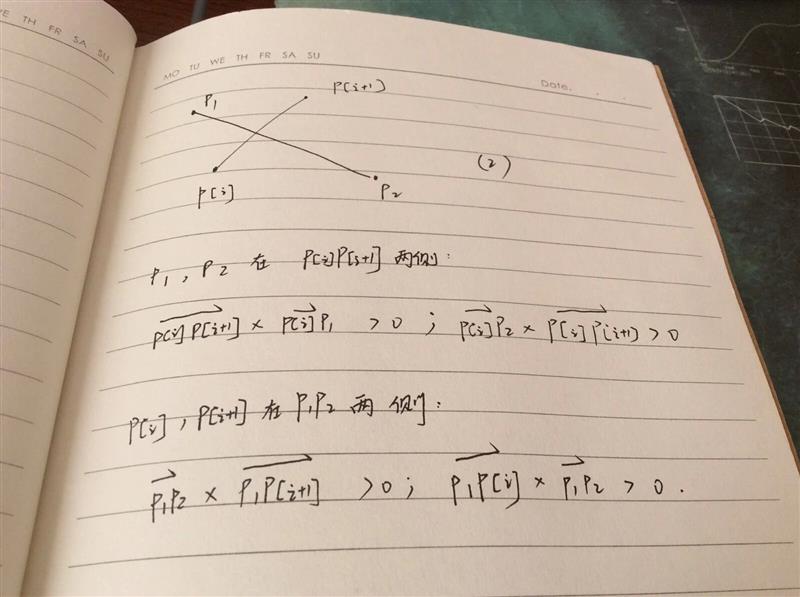
利用叉积这一工具,我们不难找到这几个点在有交点情况下的相对位置,这样我们就得到了可以判断射线和线段是否有交点的的代数表达式了。
接下来便是编程实现了,这里在编程的时候,针对过交点是否记数的问题有两种情况可以讨论,这里我们可以采用“空间换时间”的策略,遇到过交点就弃掉当前构造的射线重新生成,这样牺牲了时间复杂度但是代码相对简洁。
AC代码如下。
#include<stdio.h> #include<stdlib.h> #include<cmath> using namespace std; const double eps = 1e-10; const int offset = 1000; struct point { double x , y; }p[105] , p1 , p2; bool iszero(double x) { return fabs(x) < eps; //double不能与0直接比较 } double Crossleft(point A , point B , point C) //利用叉积判断三点的相对位置 { return (B.x - A.x) * (C.y - A.y) - (B.y - A.y)*(C.x - A.x); } int InPolygon(int n) { int cnt , i = 0; p[n] = p[0]; while(i < n) { p2.x = rand() + offset; //在很远的地方生成一个点构造射线 p2.y = rand() + offset; for(i = cnt = 0 ; i < n ; i++) { if( iszero(Crossleft(p1 , p[i] , p[i + 1])) && //所求点在多边形边上 (p[i].x - p1.x) * (p[i + 1].x - p1.x) < eps && (p[i].y - p1.y) * (p[i + 1].y - p1.y) < eps ) return true; else if(iszero(Crossleft(p1 , p2 , p[i]))) break; //射线过顶点,由于会出现两种情况,这里采取不予分析并重新生成射线 else if(Crossleft(p[i] , p[i + 1] , p1) * Crossleft(p[i] , p2 , p[i + 1]) > eps && Crossleft(p1 , p2 , p[i+1]) * Crossleft(p1 , p[i] , p2) > eps) cnt++; //射线与边相交 } } return cnt & 1; } int main() { int T , n; while(scanf("%d", &n)!= EOF) { for(int i = 0;i < n;i++) scanf("%lf%lf" , &p[i].x , &p[i].y); scanf("%d",&T); while(T--) { scanf("%lf%lf" , &p1.x , &p1.y); if(InPolygon(n)) printf("Yes\n"); else printf("No\n"); } } }
关于线段相交问题。
题目大意:给你n条线段(给你两端点的坐标以确定这条线段),然后让你确定共有多少个不同的交点。 数理分析:显然这里想得到全部的交点个数,我们需要设置穷举,然后一组一组的进行运算看能不能交到一起,那么现在的问题就是,两条已知的线段,你如何计算出二者是否相交。 我们想可以想到他们不相交的情况,通过做图不难发现。
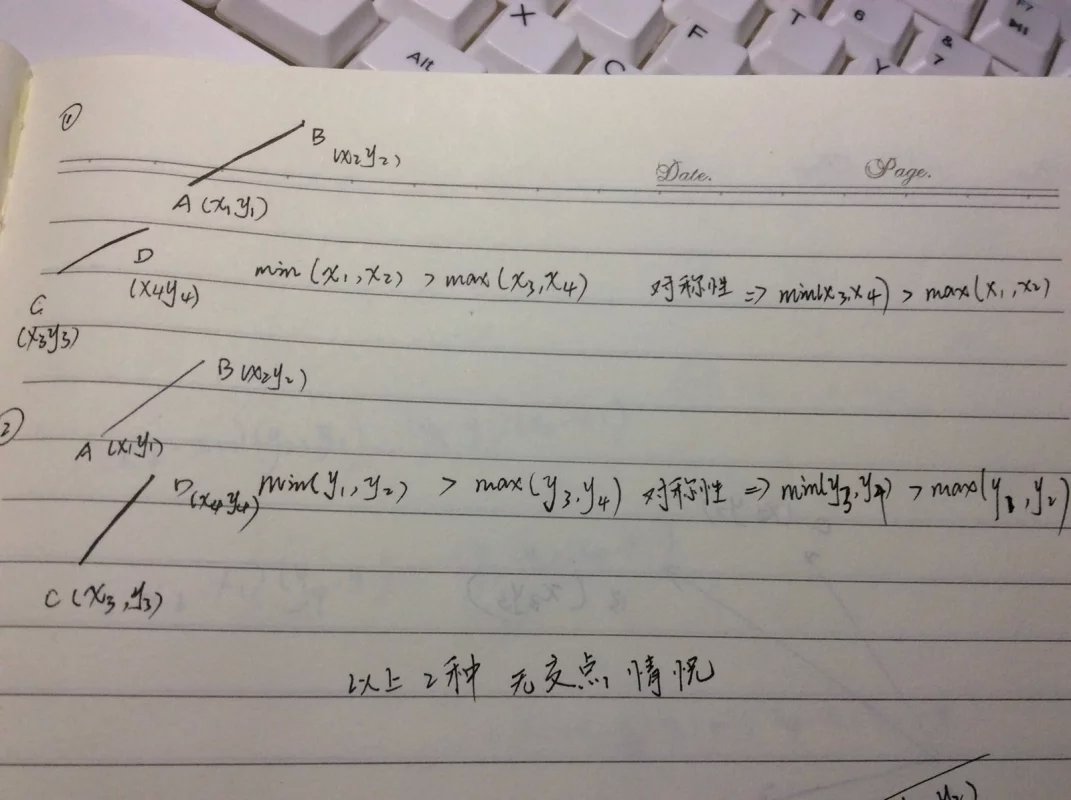
也就是说,一旦满足上面的条件,那么一定是不存在交点的,可以直接进行下一组的判断。 随后我们再思考两线段相交需要满足怎样的条件。 这里通过作图,我们发下,当A、B分别在线段CD的两边,且C、D分别在线段AB的两边的时候,两个线段是相交的。 而既然满足了这种关系,我们再借助向量这一有用的工具,给线段赋予向量的含义,然后再结合向量的叉乘,我们不难得出点坐标之间的代数运算式,于是,线段与线段之间的位置关系,就转化成了线段的端点的点坐标之间的代数关系,这一步重要的转化也为编程的实现做出了奠定了基础。
简略的证明如下(定义向量的方法是不唯一的,因子后面的代数运算式也会呈现出多样性)
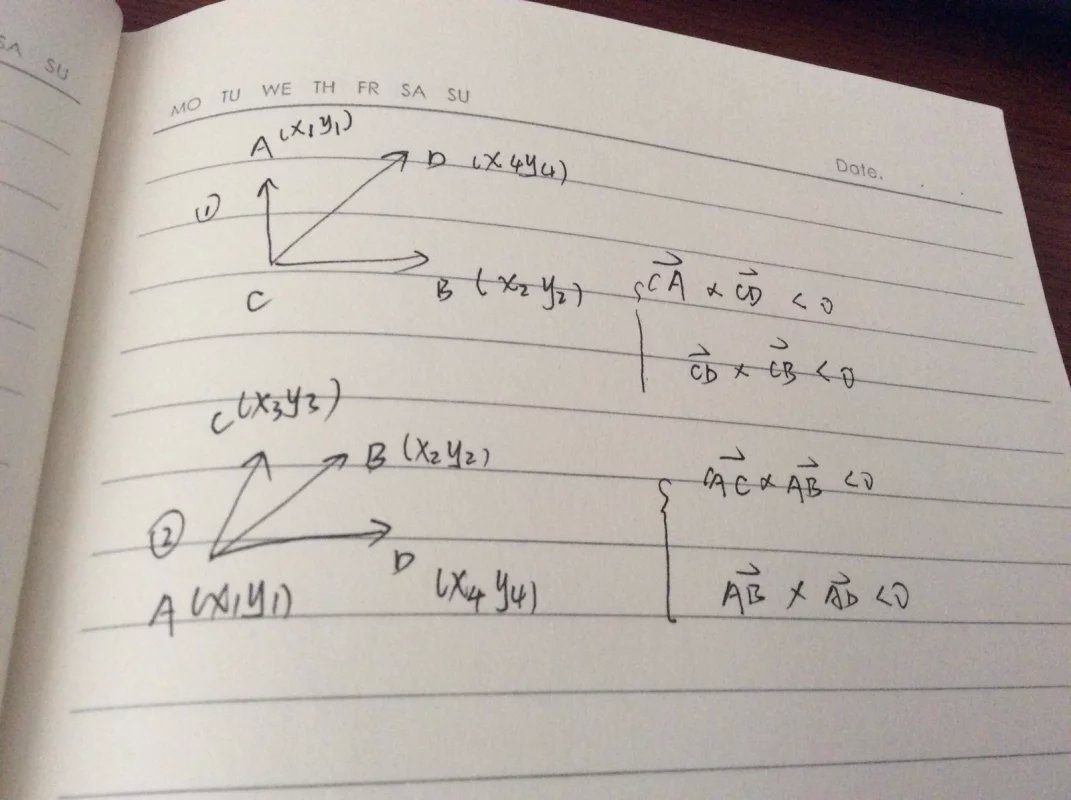
有了以上的数理分析,我们可以写出代码。
#include<stdio.h> #include<math.h> using namespace std; const double eps=1e-10; struct point { double x, y; }; double find_max(double a , double b) { return a > b ? a : b;} double find_min(double a , double b) { return a < b ? a : b;} bool if_intersect(point a ,point b , point c , point d) { if(find_min(a.x , b.x) > find_max(c.x , d.x) || find_min(a.y , b.y) > find_max(c.y , d.y) || find_min(c.x , d.x) > find_max(a.x , b.x) || find_min(c.y ,d.y) > find_max(a.y , b.y)) return 0; double h , i , j , k; h = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x); i = (b.x - a.x) * (d.y - a.y) - (b.y - a.y) * (d.x - a.x); j = (d.x - c.x) * (a.y - c.y) - (d.y - c.y) * (a.x - c.x); k = (d.x - c.x) * (b.y - c.y) - (d.y - c.y) * (b.x - c.x); return h * i <= eps && j * k <= eps; } int main() { point p[105][2]; int i , j , n; while(scanf("%d",&n) != EOF && n) { int sum = 0; for(i = 0;i < n;i++) scanf("%lf%lf%lf%lf", &p[i][0].x, &p[i][0].y, &p[i][1].x, &p[i][1].y); for(i = 0;i < n - 1;i++) for(j = i + 1;j < n;j++) if(if_intersect(p[i][0] , p[i][1] , p[j][0] , p[j][1])) sum++; printf("%d\n",sum); } }
让我们再来看一道关于线段相交的问题。(Problem source :hdu2150)

题目大意:就是给你还有ki个端点的折线n条,让你判断这些折线是否有交点。
数理分析:既然是判断折线段而且还是多条折线段是否有交点,我们拨开层层迷雾,看到这个大问题的最基元的问题——如何判断两条线段是否有交点。说到这,相信很多读者已经恍然大悟了,因为两条线断,包含着四个点,利用叉积判断其相对位置,我们在上面的一个问题(hdu 1756)中已经讨论过了。而在这里,我们介绍出它原本的学名——跨立实验。
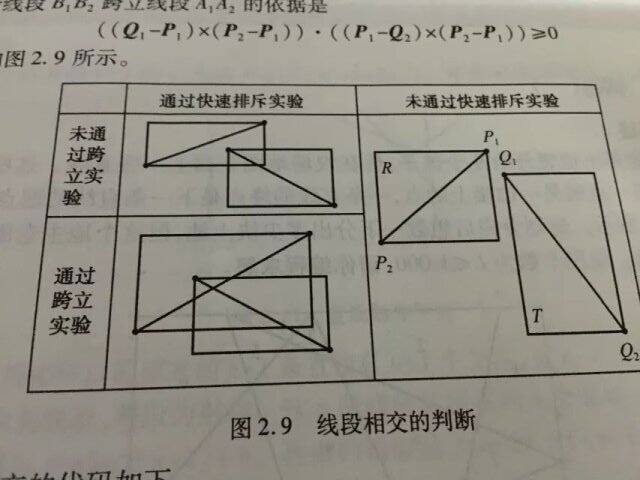
可以看到这里还有一个所谓的快速排斥实验,其实它是基于跨立实验的一步优化,它的计算量小,能够快速在跨立实验之前筛掉一些不相交的情况。(跨立实验笔者在之前的文章也讨论过,不过当时没有引出这个名词)
有了以上的数理思维的铺垫,在编程实现的时候,只需简单的设置多层循环进行端点的穷举遍历即可。
AC代码如下。
#include<stdio.h> #include<algorithm> using namespace std; const int maxn1 = 30 + 5; const int maxn2 = 100 + 5; int s[maxn1]; struct point { double x , y; }p[maxn1][maxn2]; double Crossleft(point A , point B , point C) //叉积表示四点相对位置,也是跨立实验的基础 { return (B.x - A.x)*(C.y - A.y) - (B.y -A.y)*(C.x - A.x); } bool Intersect(point A , point B , point C , point D) { if(max(A.x , B.x) >= min(C.x , D.x) && //快速排斥实验 max(C.x , D.x) >= min(A.x , B.x) && max(A.y , B.y) >= min(C.y , D.y) && max(C.y , D.y) >= min(A.y , B.y) && Crossleft(A , B , C) * Crossleft(A , D , B) >= 0 && Crossleft(C , D , A) * Crossleft(C , B , D) >= 0) //跨立实验 return 1; else return 0; } bool ok(int n) //遍历 { int k1 , k2 , i , j; for(k1 = 1;k1 < n;k1++) for(k2 = k1 + 1;k2 <= n;k2++) for(i = 1;i < s[k1] ; i++) for(j = 1;j < s[k2];j++) if(Intersect(p[k1][i] , p[k1][i+1] , p[k2][j] , p[k2][j+1])) return 1; return 0; } int main() { int n , i , j; while(scanf("%d",&n) != EOF) { for(i = 1;i <= n;i++) { scanf("%d",&s[i]); for(j = 1;j <= s[i] ; j++) scanf("%lf %lf" , &p[i][j].x , &p[i][j].y); } if(n == 1) printf("No\n"); else printf("%s\n" , ok(n) ? "Yes" : "No"); } }
让我们再看一道关于线段相交的问题。(Problem source : hdu 1147)

题目大意:依次n条线段(序号为1~n),然后按照输入的顺序依次往坐标纸上放置该线段,需要你找到所有位于最顶端的线段的序号。 基于这道题目几乎没有数理思维上的难度,我们直接分析它如何用编程来实现。 编程实现:虽然这道题需要用到判断线段相交的算法,但是怎么恰到好处的用也是接到这道题目的关键。 基于我们要按照输入的顺序放置线段,我们来模拟这个过程。显然我们要开辟一个数组来记录位于顶端的线段。这个过程肯定要和穷举这种基本方法有联系,那么我们就从中间过程分析起,以便我们更加容易的设置循环来实现穷举。 假设我们开的数组f[]来记录顶端的线段,此时我们已经完成了i条线段的放置,那么现在开始放置第i + 1条线段。那么此时我们就需要清空f[],并依次遍历判断f[]中第j条线段是否和第i + 1条线段相交,如果不相交,那么就将这第j个元素再次加入到f[]当中,遍历完成后,还需要将第i条线段加入到f[]当中。这个过程中可能会筛掉f[]中和第i + 1条线段相交的线段,所以我们需要一个新的变量q作为f[]的下标,同时q也是放置第i + 2条线段时遍历f[]数组的一个参量,但是此时我们需要初始化q为0,所以在上一次循环当中,我们用一个中间变量p来记录q的值。
有了上述对求解过程的模拟,我们就可以编程实现了。
参考代码如下。
#include<stdio.h> #include<algorithm> using namespace std; const int maxn = 100001; struct stick { double x1,y1,x2,y2; int No; }f[maxn],e[maxn]; double cross(double x1,double y1,double x2,double y2) { return x1*y2 - x2*y1; } int Find(stick a , stick b) //判断两线段相交,其实满足跨立实验一定会满足快速排斥实验 { double c[4]; //因此为了使代码更加简洁,这里只进行了跨立实验 c[0] = cross(a.x2-a.x1,a.y2-a.y1,b.x1-a.x1,b.y1-a.y1); c[1] = cross(a.x2-a.x1,a.y2-a.y1,b.x2-a.x1,b.y2-a.y1); c[2] = cross(b.x2-b.x1,b.y2-b.y1,a.x1-b.x1,a.y1-b.y1); c[3] = cross(b.x2-b.x1,b.y2-b.y1,a.x2-b.x1,a.y2-b.y1); if(c[0]*c[1] <= 0 && c[2]*c[3] <= 0) return 1; else return 0; } int main() { int n; int i , j , p , q; while(~scanf("%d",&n) , n) { for(i = 0;i < n;i++) { scanf("%lf%lf%lf%lf",&e[i].x1,&e[i].y1,&e[i].x2,&e[i].y2); e[i].No = i + 1; } p = 0; for(i = 0;i < n;i++) { q = 0; for(j = 0;j < p;j++) if(!Find(f[j],e[i])) f[q++] = f[j]; f[q++] = e[i]; p = q; } printf("Top sticks: %d",f[0].No); for(i = 1;i < p;i++) printf(", %d",f[i].No); printf(".\n"); } return 0; }
让我们再看一道基础性的计算几何问题。(Problem source : hdu4082)


题目大意:就是给出你n个点,每3个点构成的三角形彼此直线如果相似,那么就归入到一个相似三角形系当中(这里面所有的三角形都彼此相似),那么现在需要你找出这些相似三角形系中含有的最多元素是多少。
数理分析:我们将问题基元话,转化成这样一个小问题——如何判断两个三角形是否相似呢?
由于给出的三角形是关于点的坐标,我们容易将其转化成边长,随后我们容易想到三角形中一条表征边和角关系的定理——余弦定理,利用它和反三角函数,我们能较为简便的得到一个三角形的三个角。那么再判断两个三角形是否相似,就轻松多了。
编程实现:这道题虽然在数理分析上不是很困难,但是编程实现上需要注意的小细节还是很多的。下面是两个比较总要的细节。
①遇到重复出现的点如何处理?(这将为后设置穷举打下铺垫)
②构造的三角形退化成直线如何处理?(显然是剔除掉)
考虑到以上两点编程细节,接下来只需运用基础的编程思想——穷举,来完成所有情况的遍历即可。
参考代码如下。
#include<stdio.h> #include<string.h> #include<math.h> #include <algorithm> using namespace std; const int maxn = 8005; const double eps = 1e-6; struct point { int x , y; bool use; }p[20]; struct Triangle { double ang[3]; }t[maxn]; double dis(point a , point b) { return sqrt((double)(a.x - b.x)*(a.x - b.x) +(a.y - b.y)*(a.y - b.y)); } bool if_triangle(double a , double b , double c) { if(a + b <= c) return 0; else if(a + c <= b) return 0; else if(b + c <= a) return 0; else return 1; } bool ok(Triangle a , Triangle b) { if(fabs(a.ang[0] - b.ang[0]) < eps && fabs(a.ang[1] - b.ang[1]) < eps) return 1; else return 0; } int main() { int flag[maxn] , record[205][205]; int n; double a , b , c; while(scanf("%d" , &n) != EOF && n) { for(int i = 0;i < n;i++) p[i].use = false; memset(record , 0 , sizeof(record)); for(int i = 0;i < n;i++) { scanf("%d %d",&p[i].x , &p[i].y); int tx = p[i].x + 100; int ty = p[i].y + 100; if(!record[tx][ty]) { p[i].use = true; record[tx][ty] = 1; } } int index = 0; for(int i = 0;i < n;i++){ if(!p[i].use) continue; for(int j = i + 1;j < n;j++){ if(!p[j].use) continue; for(int k = j + 1;k < n;k++){ if(!p[k].use) continue; a = dis(p[i],p[k]); b = dis(p[i],p[j]); c = dis(p[j],p[k]); if(if_triangle(a , b , c)) { t[index].ang[0] = acos((a*a + b*b - c*c)/(2*a*b)); t[index].ang[1] = acos((b*b + c*c - a*a)/(2*b*c)); t[index].ang[2] = acos((a*a + c*c - b*b)/(2*a*c)); sort(t[index].ang , t[index].ang + 3); index++; } } } } memset(flag , 0 , sizeof(flag)); int Max = 0; for(int i = 0;i < index;i++) { if(flag[i]) continue; flag[i] = 1; int temp = 0; for(int j = i ;j < index;j++) { if(ok(t[i] , t[j])) { flag[j] = 1; temp++; if(temp > Max) Max = temp; } } } printf("%d\n",Max); } }
我们再来看一道关于圆的基础计算几何题目。(Problem source : hdu1798)

题目大意:分别给出两个圆的圆心坐标和半径,让你求解他们相交部分的面积。
数理分析:很简单的一道数学题,这里运用到最基础的数学分析思维——分类讨论,进行逐一分析即可。
情况1:内切or内含,此时相交面积是小圆的面积。
情况2:外切or相离,此时相交面积是0。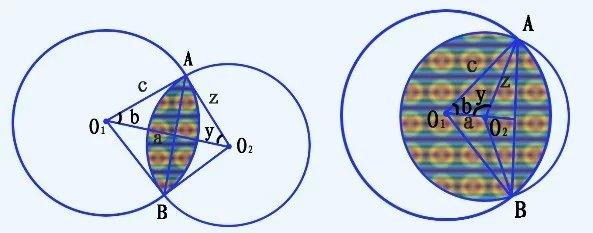
情况3:相交,这里我们表面上看,我们需要考虑俩圆心位于公共弦的同侧和异侧两种情况。那这里我们不妨分别来看一下这两种情况。
①对应左图,s = s扇形(O1AB) - s三角(O1AB) + s扇形(O2AB) - s三角(O2AB)
②对应右图,s = s扇形(O1AB) - s三角(O1AB) + s扇形(O2AB) + s三角(O2AB)。
综合上面两种情况,我们不难发现,其实都可以表示成两个圆对应的扇形趋于减去两个圆心和两个公共点组成的四边形的面积(ABO1O2)。
这里求四边形的面积,我们通过s三角(AO1O2) + s三角(BO1O2)来间接实现。
编程实现上,对于用到的PI以及一些反三角的计算,直接调用库函数即可。
参考代码如下。
#include<stdio.h> #include<cmath> const double PI = acos(-1.0); using namespace std; int main() { double x1,y1,r1,x2,y2,r2; double b , z; double sector1 , sector2; double dis; while(scanf("%lf%lf%lf",&x1,&y1,&r1) != EOF) { scanf("%lf%lf%lf",&x2,&y2,&r2); dis = sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)); if(r1 + r2 <= dis || r1 == 0 || r2 == 0) printf("0.000\n"); else if(fabs(r1-r2) >= dis) printf("%.3lf\n", r1 < r2 ? PI*r1*r1 : r2*r2*PI); else { double a1 = acos((r1*r1 + dis*dis - r2*r2)/(2*r1*dis)); double a2 = acos((r2*r2 + dis*dis - r1*r1)/(2*r2*dis)); sector1 = a1*r1*r1; sector2 = a2*r2*r2; double tri1 = r1*r1*sin(a1)*cos(a1); double tri2 = r2*r2*sin(a2)*cos(a2); printf("%.3lf\n",sector1+sector2-tri1-tri2); } } }
以上是关于计算几何及其应用——计算几何基础的主要内容,如果未能解决你的问题,请参考以下文章