数学：lucas定理的总结

Posted 2020-08-17 既然选择了远方，便只顾风雨兼程

　　今天考试的题目中有大组合数取模，不会唉，丢了45分，我真是个弱鸡，现在还不会lucas。

　　所以今天看了一下，定理差不多是：

（1）Lucas定理：p为素数，则有:

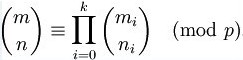
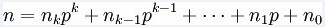
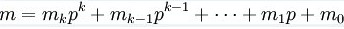
　　即：lucas(n,m,p)=c(n%p,m%p)*lucas(n/p,m/p,p) 　　然后留下我的理解：

　　用递归的方式去证明这个式子；

　　先考虑阶乘，在%p的意义下，x!=(p!^(x/p))*(x/p)!*(x%p)!这里把有p因子的数不模p，用于组合数的‘抵消’。

　　在看到组合数 :

　　　C(x,y)=x!/((x-y)!*y!)

　　　　　　=(p!^(x/p))*(x/p)!*(x%p)!/((p!^((x-y)/p))*((x-y)/p)!*((x-y)%p)!*(p!^(y/p))*(y/p)!*(y%p)!)

　　　　　　=p!^((x/p)-(x-y)/p)-y/p)*C(x/p,y/p)*C(x%p,y%p)

　　　发现这个式子和定理很像了，下面讨论一下：

　　　　1.(x/p)-(x-y)/p)-y/p=0 这样是符合的

　　　　2.(x/p)-(x-y)/p)-y/p=1 这时值要为0，式子貌似不符合，咋办？要相信我们的数学家们，分析一下，满足这个条件的话，还要满足：x%p<(x-y)%p+y%p注意是小于号，仔细体会一下不难得到：x%p小于(x-y)%p，y%p中的任意一个；这样的话，C(x%p,y%p)必定等于0，所以不影响答案。