#树# #线段树#

Posted 2020-08-17

线段树

                      

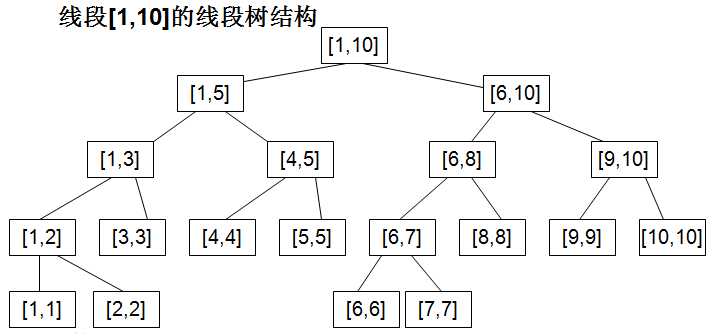
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

 

模板：

建树

 1 void Pushup(int rt){//根节点求和 
 2     segtree[rt]=segtree[rt<<1]+segtree[rt<<1|1];
 3 }
 4 
 5 void build(int l,int r,int rt){//建树
 6     if(l==r){
 7         scanf("%d",&segtree[rt]);
 8         return;
 9     }
10     int mid=l+r>>1;
11     build(l,mid,rt<<1);
12     build(mid+1,r,rt<<1|1);
13     Pushup(rt);
14 }

 

单点修改

 1 void Pushup(int rt){//根节点求和 
 2     segtree[rt]=segtree[rt<<1]+segtree[rt<<1|1];
 3 }
 4 
 5 void update(int p,int x,int l,int r,int rt){//单点修改 
 6     if(l==r){
 7         segtree[rt]+=x;//segtree[rt]=x;
 8         return;
 9     }
10     int mid=l+r>>1;
11     if(p<=mid)update(p,x,l,mid,rt<<1);
12     else update(p,x,mid+1,r,rt<<1|1);
13     Pushup(rt);
14 }

 

区间求和

int query(int L,int R,int l,int r,int rt){//区间求和 
    if(l>=L&&r<=R)return segtree[rt];
    int mid=l+r>>1;
    int ans=0;
    if(L<=mid)ans+=query(L,R,mid,l,rt<<1);
    if(R>mid)ans+=query(L,R,mid+1,r,rt<<1|1);
    return ans;
}

 

区间最小值

 1 void Pushup(int rt){//
 2     segtree[rt]=min(segtree[rt<<1],segtree[rt<<1|1]);
 3 }
 4 
 5 void build(int l,int r,int rt){//建树
 6     if(l==r){
 7         scanf("%d",&segtree[rt]);
 8         return;
 9     }
10     int mid=l+r>>1;
11     build(l,mid,rt<<1);
12     build(mid+1,r,rt<<1|1);
13     Pushup(rt);
14 }
15 
16 int query(int L,int R,int l,int r,int rt){//区间求最小值 
17     if(l>=L&&r<=R)return segtree[rt];
18     int mid=l+r>>1;
19     int ans=6452389;
20     if(L<=mid)ans=min(ans,query(L,R,l,mid,rt<<1));
21     if(R>mid) ans=min(ans,query(L,R,mid+1,r,rt<<1|1));
22 }

 

区间最大值

 1 void Pushup(int rt){
 2     segtree[rt]=max(segtree[rt<<1],segtree[rt<<1|1]);
 3 }
 4 
 5 void build(int l,int r,int rt){//建树
 6     if(l==r){
 7         scanf("%d",&segtree[rt]);
 8         return;
 9     }
10     int mid=l+r>>1;
11     build(l,mid,rt<<1);
12     build(mid+1,r,rt<<1|1);
13     Pushup(rt);
14 }
15 
16 int query(int L,int R,int l,int r,int rt){//区间求最大值 
17     if(l>=L&&r<=R)return segtree[rt];
18     int mid=l+r>>1;
19     int ans=6452389;
20     if(L<=mid)ans=max(ans,query(L,R,l,mid,rt<<1));
21     if(R>mid) ans=max(ans,query(L,R,mid+1,r,rt<<1|1));
22 }

 

区间修改

 1 void Pushup(int rt){//根节点求和 
 2     segtree[rt]=segtree[rt<<1]+segtree[rt<<1|1];
 3 }
 4 
 5 void Pushdown(int rt,int len){//向下更新
 6     if(add[rt]){
 7         add[rt<<1]+=add[rt];
 8         add[rt<<1|1]+=add[rt];
 9         segtree[rt<<1]+=add[rt]*(len-(len>>1));
10         segtree[rt<<1|1]+=add[rt]*(len>>1);
11         add[rt]=0;
12     }
13 }
14 
15 void update(int L,int R,int x,int l,int r,int rt){//区间修改 
16     if(l>=L&&r<=R){
17         add[rt]+=x;
18         segtree[rt]+=x*(r-l+1);
19         return;
20     }
21     Pushdown(rt,r-l+1);
22     int mid=l+r>>1;
23     if(L<=mid)update(L,R,x,l,mid,rt<<1);
24     if(R>mid)update(L,R,x,mid+1,r,rt<<1|1);
25     Pushup(rt);
26 }