0-1背包问题

Posted 2020-08-17 JackGo

问题：

　　给定n种物品和一背包。物品 i 的重量是 wi ，其价值是 vi ，背包的容量为 c 。

　　对于一件物品，只有装或者不装，因此该问题称为 0-1背包问题。

　　问如何选择装入背包中的物品，使得装入背包中的物品总价值最大。

分析：

　　从题目中可以提取出这几个家伙：物品集合{n种物品 ： 1 2 3 …… i …… n},背包容量c

　　把问题一般化了，就是：物品集合{n种物品 ： 1 2 3 …… i},当前背包容量 j

　　这时就可以开始递归地定义最优解了

　　用 m( i , j ) 来表示可选物品为 i ， i+1 ， …… ， n 而背包容量只剩下 j 时最优选择后背包中物品的价值。

　　（也可以用 m( i , j ) 表示选取前i件物品时，背包容量为 j 的最优物品价值，递归定义和下面的相仿）

　　这时， m( i , j ) 递归定义如下：

　　

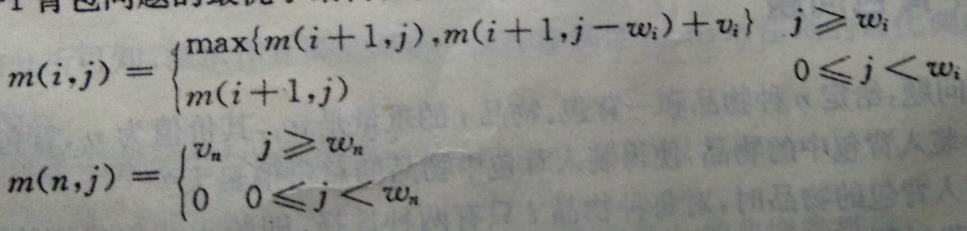
　　就是说，如果容量够装的下 i ，看下第 i 个物品装之后背包的价值大，还是不装背包价值大。 

　　

算法思路：

　　我们先计算第 n 个物品的，再计算 n-1 的，直至最上面的。

　　既然递归是要从第一件物品（即m(1,c)）开始向下那么动态规划就要反其道而行，从m(n,j)开始来，直到计算到m(1,c)

代码： 

　　

void Knapack(int v[], int w[], int c, int n, int **m)
{
    int jMax = min(w[n] - 1, c);  
    for (int j = 0; j <= jMax; j++)//如果背包容量小于 n 的大小
    {
        m[n][j] = 0;    //则装不下 n
    }

    for (int j = w[n]; j <= c; j++)//如果背包容量大于 n 的大小
    {
        m[n][j] = v[n];        //则装得下 n
    }

    for (int i = n - 1; i>1; i--)
    {
        jMax = min(w[i] - 1, c);
        for (int j = 0; j <= jMax; j++)//如果背包容量小于 i 的大小  
        {
            m[i][j] = m[i + 1][j];//则不能装 i ，只好继续装后面的  
        }

        for (int j = w[i]; j <= c; j++) //如果背包容量大于 i 的大小  
        {
            m[i][j] = max(m[i + 1][j], m[i + 1][j - w[i]] + v[i]);//则看下到底装 i 会比较好，还是不装比较好   
        }
    }
    //这边需要特殊考虑一下
    m[1][c] = m[2][c];
    if (c >= w[1])
    {
        m[1][c] = max(m[1][c], m[2][c - w[1]] + v[1]);
    }
}

void Traceback(int m[][10],int w[],int c,int n,int x[])  
{  
    for(int i=1; i<n; i++)  
    {  
        if(m[i][c] == m[i+1][c])  
        {  
            x[i]=0;  
        }  
        else  
        {  
            x[i]=1;  
            c-=w[i];  
        }  
    }  
    x[n]=(m[n][c])?1:0;  
}